Алгебра в исламском мире

В начале IX века аль-Хорезми в своей работе «Краткая книга об исчислении путем восполнения и уравновешивания» предложил новаторский подход, не основывающийся на какой-либо предыдущей «арифметической» традиции, включая Диофанта. Он разработал новую терминологию для алгебры, отличая чисто алгебраические термины от тех, что используются в арифметике. Аль-Хорезми заметил, что представление чисел имеет важное значение в повседневной жизни, поэтому он стремился найти или обобщить способы упрощения математических операций, что впоследствии стало называться алгеброй^[5].

Работа аль-Хорезми была сосредоточена на линейных и квадратных уравнениях. Он признавал, что дискриминант должен быть положительным^[7]. При этом игнорировались виды уравнений, где при положительных коэффициентах могли возникнуть неположительные корни. В самих уравнениях отрицательные коэффициенты не допускались — только много веков спустя в 1544 году они были учтены Михаэлем Штифелем, что позволило ещё больше обобщить и снизить количество типов уравнений. Также внимание уделялось элементарной арифметике двучленов и трёхчленов.

Его доказательство правила решения квадратных уравнений вида ${\displaystyle ax^{2}+bx=c}$ стало выдающимся достижением в истории алгебры. Этот прорыв заложил основу для систематического подхода к решению квадратных уравнений, ставшего фундаментальным аспектом дальнейшего развития алгебры^[8]. Подход аль-Хорезми не только предоставил практическое решение для уравнений такого типа, но и, в отличие от Диофанта, ввёл абстрактный и обобщённый подход к математическим задачам^[9].

Его подход, включающий решение уравнений с использованием радикалов и связанных с ними алгебраических вычислений, оказал влияние на математическое мышление на долгое время после его смерти. «Краткая книга об исчислении путем восполнения и уравновешивания» была переведена на латинский язык в XII веке. Этот перевод сыграл ключевую роль в передаче алгебраических знаний в Европу, значительно повлияв на математиков эпохи Возрождения и сформировав эволюцию современной математики^[8].

Большую роль в распространении арабоязычной математики на Запад сыграли практичность и универсальность методов аль-Хорезми. Они были разработаны для преобразования числовых и геометрических задач в уравнения в нормальной форме, что приводило к каноническим формулам решений^[11]. Само слово «алгебра» произошло от арабского «аль-джабр» и означало операцию переноса вычитаемых из одной части уравнения в другую с противоположным знаком, и его буквальный смысл — «восполнение»^[12].

Египетский математик Абу Камил (850—930) расширил алгебру на множество иррациональных чисел, принимая квадратные корни и корни четвёртой степени в качестве решений и коэффициентов уравнений. Также он разработал методы, используемые для решения системы из трёх нелинейных уравнений с тремя неизвестными. Одной из уникальных черт его работ была попытка найти все возможные решения некоторых из его задач, включая одну, в которой он нашёл 2676 решений^[13]. По словам Джона Леннарта Берггрена, одной из самых интересных задач, которая демонстрирует его «виртуозное» владение алгеброй, является система нелинейных уравнений с тремя неизвестными:

${\displaystyle {\begin{cases}10=x+y+z\\z^{2}=x^{2}+y^{2}\\xz=y^{2}\end{cases}}}$

Он подробно описал шаги расчёта и нашёл одно из решений данной системы^[14]. Его Алгебра, задуманная как комментарий к труду аль-Хорезми, содержит многочисленные достижения в алгебраических преобразованиях. Среди прочего, он показал правила умножения выражений, содержащих неизвестное, и правила вычисления корней, например: ${\displaystyle {\sqrt {a}}\cdot {\sqrt {b}}={\sqrt {a\cdot b}}}$. Он провёл тщательные доказательства для элементарных преобразований, таких как ${\displaystyle ax\cdot bx=ab\cdot x^{2}}$^[15]. Его работы стали важным фундаментом для развития алгебры и оказали влияние на последующих математиков^[16].

Дальнейшие достижения в алгебре были сделаны аль-Караджи (953—1029) в его трактате аль-Фахри, где он расширяет методологию, включая целые степени и целые корни неизвестных величин^[17]. Он первым систематизировал алгебраические операции с одночленами и многочленами^[18] и полностью отделил алгебру от геометрии, отбросив греческий подход к математике, основанный преимущественно на геометрии^[19]. Некоторые из задач аль-Фахри были повторно использованы Фибоначчи, Леонардо да Винчи и Джероламо Кардано без указания автора^[20][21]. В этой же книге появляется прототип доказательства методом математической индукции, аль-Караджи использовал его для доказательства формулы суммы целых кубов^[17]. Также он первым описал таблицу биномиальных коэффициентов для разложения бинома ${\displaystyle (a+b)^{n}}$^[22].

Одним из важных открытий аль-Караджи было правило:

${\displaystyle {\sqrt {{\sqrt {A}}\pm {\sqrt {B}}}}={\sqrt {\frac {{\sqrt {A}}+{\sqrt {A-B}}}{2}}}\pm {\sqrt {\frac {{\sqrt {A}}-{\sqrt {A-B}}}{2}}}}$

В своей книге «Чудесное об арифметике» он предложил читателям самостоятельно формировать иррациональности подобного вида. Историк математики Пол Люкей отмечает, что если бы у аль-Караджи нашлись последователи в этом вопросе, то кто-нибудь мог бы легко придти к мысли использовать в правой части приведённой формулы кубические корни. Тогда получилось бы выражение, в основном совпадающее с так называемой формулой Кардано. С помощью известных аль-Караджи вычислений, например, ${\displaystyle (a+b)^{3}}$, можно было бы доказать, что это выражение решает кубическое уравнение. Данная идея аль-Караджи получила развитие у европейских алгебраистов, творчество которых базировалось на восточном наследии^[23]. Историк математики Франц Вёпке высоко оценил аль-Караджи как «первого, кто ввёл теорию алгебраического исчисления»^[24].

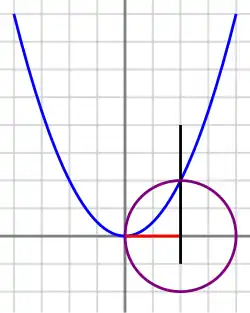
Прославленный поэт и математик Омар Хайям (1048—1131) изложил оригинальные методы решения кубических уравнений в своём сочинении «О доказательствах задач алгебры и аль-мукабалы». До Хайяма был уже известен геометрический метод, восходящий к Менехму и развитый Архимедом и Ибн аль-Хайсамом: неизвестное строилось как точка пересечения двух подходящих конических сечений. Хайям привёл обоснование этого метода, классификацию типов уравнений, алгоритм выбора типа конического сечения, оценку числа положительных корней и их величины^[25][26].

Хайям утверждал, что греки не оставили ничего в теории кубических уравнений. Как он пишет, вклад более ранних авторов, таких как Мухаммад аль-Махани и Абу Джафар аль-Хазин, заключался в переводе геометрических задач в алгебраические уравнения — что, по сути, было невозможно до работы аль-Хорезми^[25]. Арабский эклектизм способствовал сближению числовой и геометрической алгебры, а Омар Хайям продвинулся в этом направлении задолго до Декарта^[27].

В своей книге он дал первое дошедшее до нас определение алгебры как науки^[28]. Другим достижением Хайяма стало его открытие того, что кубическое уравнение может иметь более одного решения. Он показал, что существуют уравнения с двумя решениями, однако не привёл случаев, когда уравнение может иметь три вещественных корня. До формул Кардано Хайяму дойти не удалось, но он высказал надежду, что явное решение будет найдено в будущем^[25].

Аль-Самуал (1130—1180) первым определил ${\displaystyle x^{0}=1}$ и дал правило произведения любых двух одночленов целых степеней^[29]. Это позволило ему разработать эффективную процедуру, с помощью которой можно было выполнить любое деление многочленов. Например, он рассчитал:^[30]

${\displaystyle {\frac {20x^{6}+2x^{5}+58x^{4}+75x^{3}+125x^{2}+96x+94+140x^{-1}+50x^{-2}+90x^{-3}+20x^{-4}}{2x^{3}+5x+5+10x^{-1}}}}$

Шараф ад-Дин ат-Туси (1135—1213) в своей работе «Трактат об уравнениях» говорит о восьми типах кубических уравнений с положительными решениями и о пяти типах, не имеющих положительных решений. Он использовал подход, который позднее стал известен как метод «Руффини — Горнера» для численной аппроксимации корня кубического уравнения. Также он разработал концепцию производной функции и экстремумов кривой для решения кубических уравнений, которые могут не иметь положительных значений^[31]. Шараф ад-Дин понял важность дискриминанта кубического уравнения для нахождения алгебраического решения некоторых специальных видов кубических уравнений^[32].

Также он предложил идею функций, хотя и не совсем в явном виде^[33]. Он заметил, что наличие решения у кубического уравнения вида ${\displaystyle x^{2}(b-x)=d}$ зависит от того, достигает ли выражение слева значения ${\displaystyle d}$. Для определения этого он доказал, что максимум данной функции достигается в при ${\displaystyle x=2b/3}$. Таким образом, он смог утверждать, что если это значение меньше ${\displaystyle d}$, то у уравнения нет положительных решений; если оно равно ${\displaystyle d}$, то существует одно решение при ${\displaystyle x=2b/3}$; а если оно больше ${\displaystyle d}$, то существует два решения: одно в интервале от ${\displaystyle 0}$ до ${\displaystyle 2b/3}$ и другое — между ${\displaystyle 2b/3}$ и ${\displaystyle b}$^[34].

Изначально в арабоязычных работах уравнения записывались словами в виде полных предложений. Это отличалось от работы Диофанта, в которой всё же использовались некоторые символьные обозначения. Переход к современному виду алгебры, в которой используются исключительно символы, можно увидеть позднее в работах Ибн аль-Банны (1256—1321) и аль-Каласади (1412—1486), а также их предшественников^[35][36].