Арифметическая производная (производная Лагариаса , числовая производная ) — функция, определённая для целых чисел , основанная на факторизации целых чисел , таким образом, что для неё действует аналог правила произведения для производных . Стандартным обозначением для натурального числа
n
{\displaystyle n}
D
(
n
)
{\displaystyle D(n)}
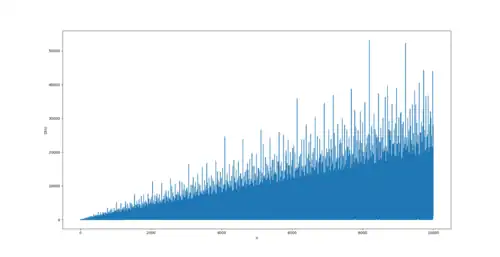
Значения
D
(
n
)
{\displaystyle D(n)}
n
{\displaystyle n}
[ 1]
D
(
0
)
=
D
(
1
)
=
0
{\displaystyle D(0)=D(1)=0}
D
(
p
)
=
1
{\displaystyle D(p)=1}
простого числа
p
{\displaystyle p}
D
(
a
b
)
=
D
(
a
)
b
+
D
(
b
)
a
{\displaystyle D(ab)=D(a)b+D(b)a}
a
,
b
∈
N
{\displaystyle a,b\in \mathbb {N} }
Область определения может быть расширена на целые числа : пользуясь тем фактом, что
D
(
1
)
=
0
{\displaystyle D(1)=0}
D
(
−
1
)
=
0
{\displaystyle D(-1)=0}
0
=
D
(
1
)
=
D
(
(
−
1
)
⋅
(
−
1
)
)
=
−
2
⋅
D
(
−
1
)
⟹
D
(
−
1
)
=
0
{\displaystyle 0=D(1)=D((-1)\cdot (-1))=-2\cdot D(-1)\implies D(-1)=0}
таким образом, для любого целого
n
{\displaystyle n}
D
(
−
n
)
=
D
(
(
−
1
)
⋅
n
)
=
D
(
−
1
)
n
+
(
−
1
)
D
(
n
)
=
−
D
(
n
)
{\displaystyle D(-n)=D((-1)\cdot n)=D(-1)n+(-1)D(n)=-D(n)}
Для арифметической производной также применимо правило производной частного двух функций (что позволяет расширить область определения до рациональных чисел ):
0
=
D
(
1
)
=
D
(
a
a
)
=
D
(
a
)
1
a
+
D
(
1
a
)
a
⟹
D
(
1
a
)
=
−
D
(
a
)
a
2
{\displaystyle 0=D(1)=D({\frac {a}{a}})=D(a){\frac {1}{a}}+D({\frac {1}{a}})a\implies D({\frac {1}{a}})=-{\frac {D(a)}{a^{2}}}}
отсюда следует:
D
(
a
b
)
=
D
(
a
)
1
b
+
D
(
1
b
)
a
=
D
(
b
)
a
b
2
−
D
(
a
)
b
=
D
(
b
)
a
−
D
(
a
)
b
b
2
{\displaystyle D({\frac {a}{b}})=D(a){\frac {1}{b}}+D({\frac {1}{b}})a={\frac {D(b)a}{b^{2}}}-{\frac {D(a)}{b}}={\frac {D(b)a-D(a)b}{b^{2}}}}
Также применимо и правило производной степени функции:
D
(
a
n
)
=
n
a
n
−
1
D
(
a
)
{\displaystyle D(a^{n})=na^{n-1}D(a)}
a
{\displaystyle a}
n
⩾
0
{\displaystyle n\geqslant 0}
D
(
p
n
)
=
n
p
n
−
1
{\displaystyle D(p^{n})=np^{n-1}}
p
{\displaystyle p}
n
⩾
0
{\displaystyle n\geqslant 0}
[ 2]
D
(
1
p
n
)
=
−
n
p
n
+
1
{\displaystyle D({\frac {1}{p^{n}}})=-{\frac {n}{p^{n+1}}}}
p
{\displaystyle p}