Исходные данные
Для некоторого момента времени  наблюдением получены высоты двух светил над горизонтом,
наблюдением получены высоты двух светил над горизонтом,  и
и  соответственно[1]. Также, из альманаха, выяснены относящиеся к этому моменту их склонения,
соответственно[1]. Также, из альманаха, выяснены относящиеся к этому моменту их склонения,  и
и  ; и гринвичские часовые углы,
; и гринвичские часовые углы,  и
и  . Северное склонение и восточная долгота считаются положительными величинами, южное склонение и западная долгота — отрицательными, в вычислениях соблюдать соглашение о знаках величин обязательно.
. Северное склонение и восточная долгота считаются положительными величинами, южное склонение и западная долгота — отрицательными, в вычислениях соблюдать соглашение о знаках величин обязательно.
Если выбранными светилами являются звёзды, у которых величины склонений и прямых восхождений можно принять неизменными в течение суток, вместо гринвичских часовых углов допустимо использовать выраженные в угловой мере значения их прямых восхождений,  , или звёздные дополнения,
, или звёздные дополнения,  . В этом случае географическая широта местоположения наблюдателя вычисляется без знания точного момента времени наблюдения светил.
. В этом случае географическая широта местоположения наблюдателя вычисляется без знания точного момента времени наблюдения светил.
Ход вычислений
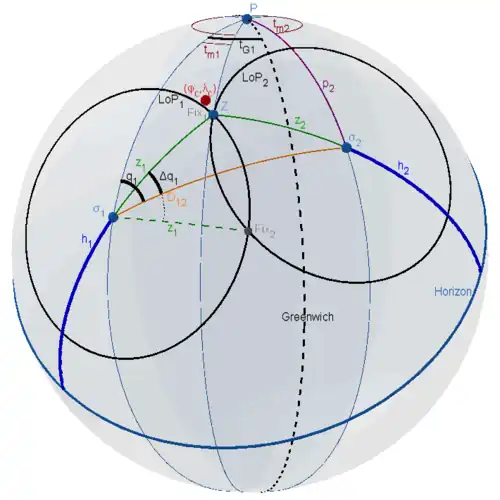
Рассмотрим параллактические треугольники  и
и  , где
, где  — северный полюс мира,
— северный полюс мира,  и
и  — наблюдаемые светила,
— наблюдаемые светила,  — зенит наблюдателя.
— зенит наблюдателя.  и
и  — зенитные расстояния светил.
— зенитные расстояния светил.
На первом этапе вычислений (определение широты) требуется величина часового угла между светилами,  , которая в случае наблюдения планет, Солнца или Луны должна быть получена из их гринвичских часовых углов:
, которая в случае наблюдения планет, Солнца или Луны должна быть получена из их гринвичских часовых углов:

При наблюдении звёзд эта величина может быть получена из значений их прямых восхождений:
![{\displaystyle \Delta t=15^{\left[{\frac {\circ }{h}}\right]}\cdot (\alpha _{2}^{[h]}-\alpha _{1}^{[h]})}](./49ec1cdf7291d1414211b4c123770a25a05d4a74.svg)
Из звёздных дополнений:

Действительные величины гринвичских часовых углов понадобятся на шаге вычисления долготы.
- Угловое расстояние между светилами,
 :
:


- Переменная часть параллактического угла,
 , от первого светила к наблюдателю:
, от первого светила к наблюдателю:

Наблюдатель может находиться в одной из двух точек,  или
или  , расположенных симметрично относительно дуги
, расположенных симметрично относительно дуги  , действительное значение паралактического угла может быть суммой или разностью углов
, действительное значение паралактического угла может быть суммой или разностью углов  и
и  .
.
- Широта первого пересечения,
 :
:

- Широта второго пересечения,
 :
:

На основании приблизительной оценки текущего местоположения наблюдателя производится выбор значения широты,  , ближайшего к ожидаемому. Дальнейшие вычисления производятся с ним.
, ближайшего к ожидаемому. Дальнейшие вычисления производятся с ним.
Знак угла  можно определить и без попытки вычисления обоих значений широты. Достаточно свериться с видом треугольника
можно определить и без попытки вычисления обоих значений широты. Достаточно свериться с видом треугольника  : если счислимое место и повышенный полюс мира находятся по одну сторону дуги
: если счислимое место и повышенный полюс мира находятся по одну сторону дуги  , величину
, величину  следует брать со знаком минус, если счислимое место и полюс мира находятся по разные стороны, — величину
следует брать со знаком минус, если счислимое место и полюс мира находятся по разные стороны, — величину  следует брать со знаком плюс.
следует брать со знаком плюс.
- Основное значение местного часового угла,
 , первого светила для широты
, первого светила для широты  :
:

Так как функция  всегда возвращает значения углов в диапазоне
всегда возвращает значения углов в диапазоне  , действительная величина местного часового угла,
, действительная величина местного часового угла,  , определяется положением светила относительно меридиана наблюдателя: если оно западнее, то
, определяется положением светила относительно меридиана наблюдателя: если оно западнее, то  , если восточнее, то
, если восточнее, то  .
.
В случае близости светила к меридиану наблюдателя — уверенно определить восточный у него азимут или западный бывает сложно, особенно для светил, расположенных около зенита. Для выбора действительного значения часового угла следует вычислить высоту второго светила, ожидаемую при обоих возможных значениях  , и сравнить с наблюдённой величиной
, и сравнить с наблюдённой величиной  .
.
 — местный часовой угол второго светила при основном значении функции
— местный часовой угол второго светила при основном значении функции 
 — местный часовой угол второго светила при втором возможном значении входной величины
— местный часовой угол второго светила при втором возможном значении входной величины
 — вычисленная высота второго светила для места
— вычисленная высота второго светила для места 
 — вычисленная высота второго светила для места
— вычисленная высота второго светила для места 
Вычисление долготы производится с тем значением часового угла,  , первого светила, при котором вычисленная,
, первого светила, при котором вычисленная,  , и наблюдённая,
, и наблюдённая,  , высота второго светила согласуются.
, высота второго светила согласуются.
- Долгота выбранного пересечения кругов равных высот,
 :
:

Географические координаты  и
и  местоположения наблюдателя на момент времени
местоположения наблюдателя на момент времени  определены.
определены.
Решение неоднозначности
Если для обсервации были доступны только два светила, например, Солнце и Луна, и устранить неоднозначность выбора координат обсервацией третьего светила невозможно, а счислимое место неизвестно даже приблизительно, надлежит вычислить азимуты одного из светил для обоих пересечений и сравнить их с наблюдёнными значениями.
- Азимут светила,
 :
:

Для выбора правильного значения широты (и, в дальнейшем, — долготы), достаточно иметь оценку азимута наблюдённого светила с допуском ±10°.
Координаты точек пересечений, по тем же исходным данным, можно вычислить[2] с помощью единственной тригонометрической функции — гаверсинус угла,  . Для получения точности координат в одну угловую минуту пригодна 4-значная таблица натуральных значений гаверсинусов[3], что позволяет произвести расчёты без применения электронных калькуляторов или таблиц логарифмов значений нескольких тригонометрических функций.
. Для получения точности координат в одну угловую минуту пригодна 4-значная таблица натуральных значений гаверсинусов[3], что позволяет произвести расчёты без применения электронных калькуляторов или таблиц логарифмов значений нескольких тригонометрических функций.
- Вспомогательные величины
 и
и  :
:


- Угловое расстояние между светилами,
 :
:





Полярное расстояние всегда отсчитывается от северного полюса мира.
- Вспомогательные величины
 ,
,  ,
,  ,
,  ,
,  и
и  :
:






- Вспомогательный угол
 :
:

- Вспомогательный угол
 :
:

- Вспомогательный угол
 , относящийся к первой точке пересечения кругов равной высоты:
, относящийся к первой точке пересечения кругов равной высоты:

- Угол, дополнительный к широте,
 , и широта первой точки пересечения,
, и широта первой точки пересечения,  :
:


Если полученное значение широты не согласуется с приближённой оценкой текущего местоположения наблюдателя, вычисляется широта второй точки пересечения кругов равной высоты:



Дальнейшие вычисления производятся с выбранным значением  .
.
- Вспомогательные величины
 и
и  :
:


- Основное значение местного часового угла,
 , первого светила, для широты
, первого светила, для широты  :
:

Так как функция  всегда возвращает значения углов в диапазоне
всегда возвращает значения углов в диапазоне  , действительная величина местного часового угла,
, действительная величина местного часового угла,  , определяется положением светила относительно меридиана наблюдателя: если оно западнее, то
, определяется положением светила относительно меридиана наблюдателя: если оно западнее, то  , если восточнее, то
, если восточнее, то  .
.
В случае близости светила к меридиану наблюдателя — уверенно определить восточный у него азимут или западный бывает сложно, особенно для светил, расположенных около зенита. Для выбора значения часового угла следует вычислить высоту второго светила, ожидаемую при обоих возможных значениях, и сравнить с наблюдённой величиной  .
.
 — местный часовой угол второго светила при основном значении функции
— местный часовой угол второго светила при основном значении функции 
 — местный часовой угол второго светила при втором возможном значении входной величины
— местный часовой угол второго светила при втором возможном значении входной величины




Дуга  — зенитное расстояние второго светила, вычисленное для места
— зенитное расстояние второго светила, вычисленное для места  .
.
 — вычисленная высота второго светила.
— вычисленная высота второго светила.
Вычисление долготы производится с тем значением часового угла,  , первого светила, при котором вычисленная,
, первого светила, при котором вычисленная,  , и наблюдённая,
, и наблюдённая,  , высота второго светила согласуются.
, высота второго светила согласуются.
- Долгота точки пересечения,
 :
:

Географические координаты  и
и  местоположения наблюдателя на момент времени
местоположения наблюдателя на момент времени  определены.
определены.
Решение неоднозначности
Если для обсервации были доступны только два светила, например, Солнце и Луна, и устранить неоднозначность выбора координат обсервацией третьего светила невозможно, а счислимое место неизвестно даже приблизительно, надлежит вычислить азимуты одного из светил для обоих пересечений и сравнить их с наблюдёнными значениями.
- Угловое расстояние светила от повышенного полюса,
 :
:

- Азимут светила,
 :
:

Для выбора правильного значения широты (и, в дальнейшем, — долготы), достаточно иметь оценку азимута наблюдённого светила с допуском ±10°.