Гипотеза о двухъярусной кровати

Гипотеза о двухъярусной кровати^[1] — это утверждение в теории перколяции, разделе математики, изучающем поведение связанных кластеров в случайном графе. Гипотеза названа так, потому что структура участвующего в ней графа похожа на двухъярусную кровать. Впервые гипотеза была высказана Питером Кастелейном в 1985 году^[2]. В 2024 году российский и американский математик Игорь Пак с коллегами нашли контрпример — граф относительно несложной конструкции, содержащий более 7000 вершин^[3].

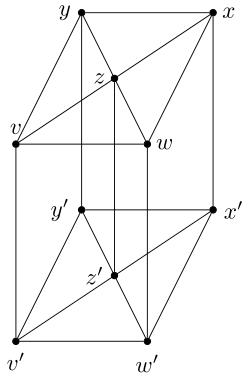
У гипотезы есть много эквивалентных формулировок^[4]. Во всех формулировках строится так называемый граф двухъярусной кровати. Граф содержит два подграфа, называемых «верхним ярусом» и «нижним ярусом». Эти графы изоморфны, то есть имеют одинаковую структуру. Некоторые вершины верхнего яруса соединяется с соответствующей вершиной нижнего яруса дополнительным ребром, которые называются «столбиками»^[3].

В самой общей формулировке рёбра случайно и независимо сохраняются (остаются открытыми) с вероятностью ${\displaystyle p_{i}}$, и теряются (перекрываются) с вероятностью ${\displaystyle 1-p_{i}}$. На обоих ярусах вероятности равны, вероятности для столбиков произвольные. При этом может случиться, что на верхнем ярусе ребро осталось, а на нижнем — перекрылось, и наоборот.

Гипотеза о двухъярусной кровати утверждает: когда у горизонтальных рёбер вероятность остаться ${\displaystyle p}$ одна и та же, а столбики всегда открыты, скорее между двумя вершинами из одного яруса сохранится путь, чем между теми же вершинами с разных ярусов. Формально:

Пусть ${\displaystyle x}$ и ${\displaystyle y}$ — вершины из одного яруса, ${\displaystyle y'}$ — изоморфная копия ${\displaystyle y}$ из второго яруса. Тогда

${\displaystyle p\{x\leftrightsquigarrow y\}\geqslant p\{x\leftrightsquigarrow y'\}}$

Когда между y и y′ есть неисчезающий столбик, то, очевидно, ${\displaystyle x\leftrightsquigarrow y\Leftrightarrow x\leftrightsquigarrow y'}$. Таким образом, чтобы гипотеза имела смысл, нужно, чтобы столбики были не везде.

Гипотеза основывается на интуиции, что при исчезновении прямого пути от x до y найдётся резервный на другом ярусе. Потерять путь от x до y′ должно быть проще — меньше кандидатов в резервные пути. Аналогичные вопросы для случайных блужданий и модели Изинга были разрешены положительно^[5][6]. Первоначальной мотивировкой для этой гипотезы была более слабая гипотеза о том что при перколяции на бесконечной квадратной решётке вероятность вершины ${\displaystyle (0,0)}$ быть связанной с ${\displaystyle (x,y)}$ при ${\displaystyle x,y\geqslant 0}$ больше, чем вероятность ${\displaystyle (0,0)}$ быть связанной с вершиной ${\displaystyle (x+1,y)}$^[5].

Из-за интуитивности гипотезы двухъярусной кровати её доказательство было активной областью исследований в теории перколяции^[7]. Гипотеза была доказана для определённых типов графов, таких как колёса,^[8] полные графы,^[9] полные двудольные графы и графы с локальной симметрией^[10]. Гипотеза также была доказана в пределе ${\displaystyle p\to 1}$ для любого графа^[11][12].

Авторы взяли более ранний контрпример Холлома для гиперграфов с разными вероятностями полностью потерять 3-гиперребро, оторвать от него «главную» вершину, и оторвать одну из двух второстепенных (столбики — обычные 2-рёбра), и сумели сымитировать каждое гиперребро большим количеством (более 2000) обычных равновероятных 2-рёбер. Полученный граф содержит 7222 вершины, 14 442 ребра и всего три столбика, вероятность сохранения ребра ${\displaystyle p=0{,}5}$, при этом разница незначительна, около 10⁻⁶⁵⁰⁰.

Для данного графа из-за относительной простоты удалось вручную оценить разницу вероятностей. Меньшие графы и бо́льшие разницы не получается найти из-за случайной природы алгоритмов: даже если уровень значимости будет 5σ (шесть девяток), ни один журнал не примет этого результата^[3].