Граф Винера — Арайи
| граф Винера — Арайи | |
|---|---|
 | |
| Вершин | 42 |
| Рёбер | 67 |
| Радиус | 5 |
| Диаметр | 7 |
| Обхват | 4 |
| Хроматическое число | 3 |
| Хроматический индекс | 4 |
| Свойства |
гипогамильтонов планарный |
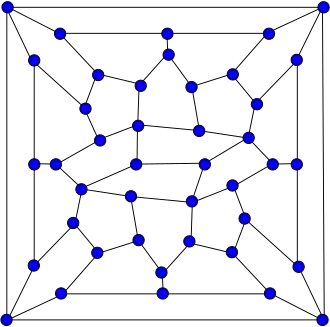
В теории графов Граф Винера — Арайи — неориентированный планарный гипогамильтонов граф с 42 вершинами и 67 рёбрами, названный в честь Габора Винера и Макото Арайи, впервые описавших его в 2009 году в публикации The ultimate question (2009)[1][2].
История
Гипогамильтоновы графы впервые были исследованы Сусилье в статье Problèmes plaisants et délectables (1963)[3]. В 1967 году Линдгрен построил бесконечную последовательность гипогамильтоновых графов[4]. Он указал на Годена, Герца и Росси[5], а затем на Ба́сакера и Саати[6] как пионеров данной области.
Минимальный по числу вершин гипогамильтонов граф был известен давно — это Граф Петерсена. Однако поиска наименьшего планарного гипогамильтонова граф продолжаются. Впервые вопрос был поставлен Вацлавом Хваталом в 1973 году[7]. Первым попытался предоставить ответ Карстен Томассен в 1976 году, его 105-граф Томассена[8] содержал 105 вершин. В 1979 году Хатцель улучшил этот результат, найдя планарный гипогамильтонов граф с 57 вершинами — граф Хатцеля[9]. Эта граница была понижена в 2007 году 48-графом Замфиреску[10].
В 2009 году граф, построенный Габором Винером и Макото Арайи, (с 42 вершинами) стал наименьшим известным планарным гипогамильтоновым графом. В своей статье[1][2] Винер и Арайа предположили, что существование их графа делает возможным, что главный вопрос жизни, вселенной и всего такого в романе Дугласа Адамса Автостопом по галактике, мог звучать как "каков размер минимального планарного гипогамильтонова графа?"
Однако уже в 2013 году был обнаружен меньший планарный гипогамильтонов граф (40 вершин)[11].
Свойства
Граф Винера — Арайи планарен. Его можно нарисовать на плоскости без пересечения рёбер.
Граф Винера — Арайи гипогамильтонов. Сам по себе граф не содержит гамильтонова цикла, однако удаление любой одной вершины приводит к графу, содержащему гамильтонов цикл.
Хроматическое число графа равно 3, хроматический индекс равен 4, обхват равен 4, радиус равен 5, диаметр равен 7.
Примечания
- 1 2 Wiener, Araya, 2009.
- 1 2 Wiener, Araya, 2011, с. 55–68.
- ↑ Sousselier, 1963, с. 405–406.
- ↑ Lindgren, 1967, с. 1087–1089.
- ↑ Gaudin, Herz, Rossi, 1964, с. 214–218.
- ↑ Busacker, Saaty, 1965.
- ↑ Chvátal, 1973, с. 33–41.
- ↑ Thomassen, 1976, с. 377–389.
- ↑ Hatzel, 1979, с. 213–216.
- ↑ Zamfirescu, Zamfirescu, 2007, с. 338–342.
- ↑ Jooyandeh, McKay, Ostergard, Pettersson, Zamfirescu, 2013.
Литература
- Gábor Wiener, Makoto Araya. The ultimate question. — 2009. — Апрель. — . — arXiv:0904.3012.
- Gábor Wiener, Makoto Araya. On planar hypohamiltonian graphs // Journal of Graph Theory. — 2011. — Т. 67, вып. 1. — С. 55–68. — doi:10.1002/jgt.20513.
- Sousselier R. Problème no. 29: Le cercle des irascibles. — Rev. Franç. Rech. Opérationnelle, 1963. — Т. 7. — С. 405–406.
- Lindgren W. F. An infinite class of hypohamiltonian graphs // American Mathematical Monthly. — 1967. — Т. 74. — С. 1087–1089. — doi:10.2307/2313617.
- Gaudin T., Herz P., Rossi. Solution du problème No. 29 (фр.) // Rev. Franç. Rech. Opérationnelle. — 1964. — Vol. 8. — P. 214–218.
- Busacker R. G., Saaty T. L. Finite Graphs and Networks. — 1965.
- Басакер Р., Саати Т. Конечные графы и сети. — М.: «Наука», 1974..
- Chvátal V. Flip-flops in hypo-Hamiltonian graphs // Canadian Mathematical Bulletin. — 1973. — Т. 16. — С. 33–41. — doi:10.4153/cmb-1973-008-9.
- Carsten Thomassen. Planar and infinite hypohamiltonian and hypotraceable graphs // Discrete Mathematics. — 1976. — Т. 14, вып. 4. — С. 377–389. — doi:10.1016/0012-365x(76)90071-6.
- Wolfgang Hatzel. Ein planarer hypohamiltonscher Graph mit 57 Knoten (Ge) // Mathematische Annalen. — 1979. — Т. 243, вып. 3. — С. 213–216. — doi:10.1007/BF01424541.
- Carol T. Zamfirescu, Tudor I. Zamfirescu. A planar hypohamiltonian graph with 48 vertices // Journal of Graph Theory. — 2007. — Т. 55, вып. 4. — С. 338–342. — doi:10.1002/jgt.20241.
- Mohammadreza Jooyandeh, Brendan D. McKay, Patric R. J. Ostergard, Ville H. Pettersson, Carol T. Zamfirescu. Planar Hypohamiltonian Graphs on 40 Vertices (англ.) // Journal of Combinatorial Theory, Series B. — 2013.
Ссылки
Weisstein, Eric W. Wiener-Araya Graph (англ.) на сайте Wolfram MathWorld.