Двойной маятник

В физике и математике, в теории динамических систем, двойной маятник определяют как маятник, состоящий из двух звеньев. Как правило, первое звено закреплено в неподвижной точке с помощью сферического или цилиндрического шарнира. Второе звено прикреплено ко второму концу первого звена в общем случае также с помощью сферического шарнира. Двойной маятник является простой физической системой, которая проявляет разнообразное динамическое поведение со значительной зависимостью от начальных условий^[1]. Движение маятника описывается обыкновенными дифференциальными уравнениями. Для некоторых энергий его движение является хаотическим.

Анализ

Можно рассматривать несколько вариантов двойных маятников: два звена могут быть одинаковыми или иметь разную длину и вес; они могут быть простыми маятниками или физическими маятниками; движение может происходить в пространстве или быть ограничено вертикальной плоскостью.

В дальнейшем анализе предполагается, что звенья — одинаковые физические маятники длины $\ell$ и массы $m$ , и их движение ограничено вертикальной плоскостью.

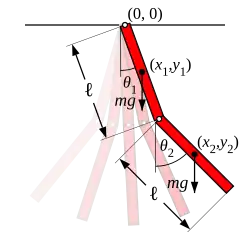
У физического маятника масса распределена вдоль всей его длины. Если масса распределена равномерно, тогда центр масс каждого звена совпадает с его геометрическим центром, и звено имеет такой момент инерции $\textstyle I={\frac {1}{12}}m\ell ^{2}$ относительно этой точки.

Для рассматриваемой системы с двумя степенями свободы удобно использовать в качестве обобщённых координат углы, которые образуют звенья с нисходящей вертикалью. Они задают точку на конфигурационном пространстве системы — двумерном торе. Если поместить начало декартовой системы координат в точку подвеса первого звена, то относительно этой системы отсчёта центр масс первого маятника находится в точке с координатами:

{\begin{cases}x_{1}={\frac {\ell }{2}}\sin \theta _{1}\\y_{1}=-{\frac {\ell }{2}}\cos \theta _{1}\end{cases}}.

Центр масс второго звена находится в точке с координатами

{\begin{cases}x_{2}=\ell \left(\sin \theta _{1}+{\frac {1}{2}}\sin \theta _{2}\right)\\y_{2}=-\ell \left(\cos \theta _{1}+{\frac {1}{2}}\cos \theta _{2}\right).\end{cases}}

Этой информации достаточно для того, чтобы выписать лагранжиан и с его помощью вывести описывающие движения уравнения Лагранжа.

Лагранжиан

{\begin{aligned}L&={\frac {1}{2}}m\left(v_{1}^{2}+v_{2}^{2}\right)+{\frac {1}{2}}I\left({{\dot {\theta }}_{1}}^{2}+{{\dot {\theta }}_{2}}^{2}\right)-mg\left(y_{1}+y_{2}\right)\\&={\frac {1}{2}}m\left({{\dot {x}}_{1}}^{2}+{{\dot {y}}_{1}}^{2}+{{\dot {x}}_{2}}^{2}+{{\dot {y}}_{2}}^{2}\right)+{\frac {1}{2}}I\left({{\dot {\theta }}_{1}}^{2}+{{\dot {\theta }}_{2}}^{2}\right)-mg\left(y_{1}+y_{2}\right),\end{aligned}}

иначе называемый функцией Лагранжа, записывается как разность кинетической энергии и потенциальной энергии. Первое слагаемое в выражении для кинетическая энергия отвечает за кинетическую энергию поступательного движения центров масс звеньев. Второе слагаемое в этом выражении определяет кинетическую энергию вращательного движения каждого из стержней вокруг его центра масс. Последнее слагаемое определяет потенциальную энергию звеньев маятника в однородном гравитационном поле.

Подставляя координаты в выражение для функции Лагранжа после перегруппировки имеем

L={\frac {1}{6}}m\ell ^{2}\left[{{\dot {\theta }}_{2}}^{2}+4{{\dot {\theta }}_{1}}^{2}+3{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\cos(\theta _{1}-\theta _{2})\right]+{\frac {1}{2}}mg\ell \left(3\cos \theta _{1}+\cos \theta _{2}\right).

Движение двойного физического маятника (из численного интегрирования уравнения движения)

При большой выдержке, двойной маятник проявляет хаотическое движение (отслежен с помощью светодиодов)

Обобщенные импульсы можно записать как

{\begin{cases}p_{\theta _{1}}\equiv {\frac {\partial L}{\partial {{\dot {\theta }}_{1}}}}={\frac {1}{6}}m\ell ^{2}\left[8{{\dot {\theta }}_{1}}+3{{\dot {\theta }}_{2}}\cos(\theta _{1}-\theta _{2})\right]\\\\p_{\theta _{2}}\equiv {\frac {\partial L}{\partial {{\dot {\theta }}_{2}}}}={\frac {1}{6}}m\ell ^{2}\left[2{{\dot {\theta }}_{2}}+3{{\dot {\theta }}_{1}}\cos(\theta _{1}-\theta _{2})\right].\end{cases}}

Эти выражения можно преобразовать, чтобы получить

{\begin{cases}{{\dot {\theta }}_{1}}={\dfrac {6}{m\ell ^{2}}}{\dfrac {2p_{\theta _{1}}-3\cos(\theta _{1}-\theta _{2})p_{\theta _{2}}}{16-9\cos ^{2}(\theta _{1}-\theta _{2})}}\\\\{{\dot {\theta }}_{2}}={\dfrac {6}{m\ell ^{2}}}{\dfrac {8p_{\theta _{2}}-3\cos(\theta _{1}-\theta _{2})p_{\theta _{1}}}{16-9\cos ^{2}(\theta _{1}-\theta _{2})}}.\end{cases}}

Уравнения движения, получаемые как уравнения Эйлера — Лагранжа, можно записать как

{\begin{cases}{{\dot {p}}_{\theta _{1}}}={\frac {\partial L}{\partial \theta _{1}}}=-{\frac {1}{2}}m\ell ^{2}\left[{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\sin(\theta _{1}-\theta _{2})+3{\frac {g}{\ell }}\sin \theta _{1}\right]\\\\{{\dot {p}}_{\theta _{2}}}={\frac {\partial L}{\partial \theta _{2}}}=-{\frac {1}{2}}m\ell ^{2}\left[-{{\dot {\theta }}_{1}}{{\dot {\theta }}_{2}}\sin(\theta _{1}-\theta _{2})+{\frac {g}{\ell }}\sin \theta _{2}\right].\end{cases}}

Последние четыре уравнения описывают динамику системы с заданным текущим состоянием — начальными координатами и начальными скоростями системы.

В общем случае эти уравнения невозможно проинтегрировать аналитически^[2],^[3] и представить формулы для θ₁ и θ₂ как явные функции от времени. Однако возможно выполнить численное интегрирование, позволяющее наблюдать динамику двойного маятника.

Некоторые задачи

Рассматривают различные задачи, в которых появляется двухзвенный маятник. Среди них

задача о движении на круговой орбите ^[4]
задача о движении на эллиптической орбите ^[5].

Примечания

↑ Levien RB and Tan SM. Double Pendulum : An experiment in chaos.American Journal of Physics 1993; 61 (11) : 1038
↑ Буров А. А. О несуществовании дополнительного интеграла в задаче о тяжелом двузвенном плоском маятнике // Прикладная математика и механика. Том 50. Вып.1. С.168-171 = A.A. Burov On the non-existence of a supplementary integral in the problem of a heavy two-link plane pendulum //Journal of Applied Mathematics and Mechanics. Volume 50, Issue 1, 1986, Pages 123—125
↑ Dullin, H.R. Melnikov’s method applied to the double pendulum. Z. Physik B — Condensed Matter 93, 521—528 (1994).
↑ V. A. Sarychev, Equilibria of a double pendulum in a circular orbit, Acta Astronautica, 44 (1999), 63-65.
↑ José Laudelino de Menezes Neto, Gerson Cruz Araujo, Yocelyn Pérez Rothen, Claudio Vidal. Parametric stability of a double pendulum with variable length and with its center of mass in an elliptic orbit. Journal of Geometric Mechanics, 2022, 14(3): 381-408.

[1] Levien RB and Tan SM. Double Pendulum : An experiment in chaos.American Journal of Physics 1993; 61 (11) : 1038

[2] Буров А. А. О несуществовании дополнительного интеграла в задаче о тяжелом двузвенном плоском маятнике // Прикладная математика и механика. Том 50. Вып.1. С.168-171 = A.A. Burov On the non-existence of a supplementary integral in the problem of a heavy two-link plane pendulum //Journal of Applied Mathematics and Mechanics. Volume 50, Issue 1, 1986, Pages 123—125

[3] Dullin, H.R. Melnikov’s method applied to the double pendulum. Z. Physik B — Condensed Matter 93, 521—528 (1994).

[4] V. A. Sarychev, Equilibria of a double pendulum in a circular orbit, Acta Astronautica, 44 (1999), 63-65.

[5] José Laudelino de Menezes Neto, Gerson Cruz Araujo, Yocelyn Pérez Rothen, Claudio Vidal. Parametric stability of a double pendulum with variable length and with its center of mass in an elliptic orbit. Journal of Geometric Mechanics, 2022, 14(3): 381-408.

[1]

[2]

[3]

[4]

[5]