Додекаэдрическая пирамида
| Додекаэдрическая пирамида | |
|---|---|
 Диаграмма Шлегеля: проекция (перспектива) правильной додекаэдрической пирамиды в трёхмерное пространство | |
| Тип | Многогранная пирамида |
| Символ Шлефли | ( ) ∨ {5,3} |
| Ячеек | 13 |
| Граней | 42 |
| Рёбер | 50 |
| Вершин | 21 |
| Двойственный политоп | Икосаэдрическая пирамида |
Додекаэдри́ческая пирами́да — четырёхмерный многогранник (многоячейник): многогранная пирамида, имеющая основанием додекаэдр.
Ограничена 13 трёхмерными ячейками — 12 пятиугольными пирамидами и 1 додекаэдром. Додекаэдрическая ячейка окружена всеми двенадцатью пирамидальными; каждая пирамидальная ячейка окружена додекаэдрической и пятью пирамидальными.
У додекаэдрической пирамиды 42 грани — 12 пятиугольников и 30 треугольников. Каждая пятиугольная грань разделяет додекаэдрическую и пирамидальную ячейки, каждая треугольная — две пирамидальных.
Имеет 50 рёбер. На каждом ребре сходятся по три грани и по три ячейки: для 30 рёбер это две пятиугольных и треугольная грани, додекаэдрическая и две пирамидальных ячейки; для остальных 20 рёбер — три треугольных грани, три пирамидальных ячейки.
Имеет 21 вершину. В 20 вершинах сходятся по 4 ребра, по 6 граней (три пятиугольных, три треугольных) и по 4 ячейки (додекаэдрическая, три пирамидальных); в 1 вершине — 20 рёбер, все 30 треугольных граней и все 12 пирамидальных ячеек.
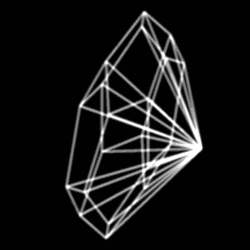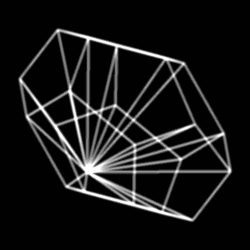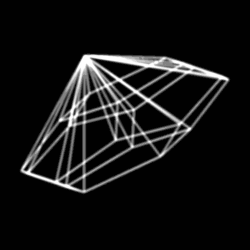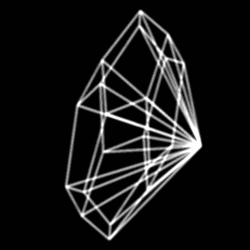
В отличие от многогранных пирамид, построенных на четырёх других платоновых телах, додекаэдрическая пирамида не может иметь все рёбра одинаковой длины.
- Пусть все рёбра додекаэдрического основания равны все боковые рёбра пирамиды равны
- Тогда пирамида — правильная, и проекция её бокового ребра на гиперплоскость основания есть радиус описанной вокруг основания сферы А поскольку проекция меньше наклонной,
- Но в правильном додекаэдре значит, и равняться эти два числа не могут.
Ссылки
- George Olshevsky. Pyramid / Glossary for Hyperspace