Квадратура круга Тарского
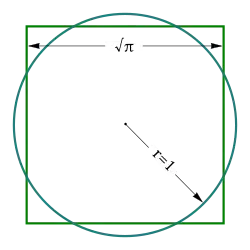
Квадрату́ра кру́га Та́рского — задача о равносоставленности круга и равновеликого квадрата, сформулированная Альфредом Тарским в 1925 году.
Формулировка
Возможно ли разрезать круг на конечное число частей и собрать из них квадрат такой же площади?
Более формально: можно ли разбить круг на конечное количество попарно непересекающихся подмножеств и передвинуть их так, чтобы получить разбиение квадрата такой же площади на попарно непересекающиеся подмножества?
История
В 1925 году задача была сформулирована польско-американским математиком Альфредом Тарским.
В 1963 году был достигнут первый прогресс в решении задачи. Лестер Дубинс, Моррис У. Хирш и Джек Каруш доказали, что равное разложение невозможно получить разрезанием вдоль жордановых кривых, то есть если разбиение Тарского существует, то оно требует сложных фрактальных кусков, испещренных дырами и замысловато зазубренными краями[1].
В 1989 году возможность такого разбиения доказал венгерский математик Миклош Лацкович.
Доказательство Лацковича опирается на аксиому выбора. Найденное разбиение состоит из примерно 1050 частей, которые являются неизмеримыми множествами и границы которых не являются жордановыми кривыми. Для перемещения частей достаточно использовать только параллельный перенос, без поворотов и отражений.
Однако доказательство Лацковича не было конструктивным, он лишь доказал, что разбиение можно сделать, но он не мог ни сказать, как построить части, ни каким-либо образом описать их.
В 2005 году Тревор Уилсон доказал, что существует требуемое разбиение, при котором части можно сдвигать параллельным переносом таким образом, чтобы они всё время оставались непересекающимися.
В 2017 году Эндрю Маркс и Спенсер Унгер нашли первое полностью конструктивное решение задачи Тарского с разбиением на 10200 борелевских кусков[2].
В 2021 году Мате, Ноэль и Пихурко улучшили свойства борелевских кусков, необходимых для конструктивного решения задачи Тарского. Хотя количество требуемых частей в новом решении осталось прежним (10200), найденные ими куски проще по форме и их намного легче визуализировать. Это открывает путь к дальнейшему упрощению разбиение и уменьшению числа кусков. Согласно предположению одного из авторов, должно существовать разбиение Тарского из 22 кусков или меньше[3][4].
См. также
Примечания
- ↑ Dubins L., Hirsch M. W., Karush J. Scissor congruence (англ.) // Israel Journal of Mathematics. — 1963. — Vol. 1, iss. 4. — P. 239–247. — doi:10.1007/BF02759727.
- ↑ Marks A., Unger S. Borel circle squaring (англ.) // Annals of Mathematics. — 2017. — Vol. 186, iss. 2. — P. 581—605. — doi:10.4007/annals.2017.186.2.4. Архивировано 11 ноября 2020 года.
- ↑ Máthé, András; Noel, Jonathan A.; Pikhurko, Oleg (3 февраля 2022). Circle Squaring with Pieces of Small Boundary and Low Borel Complexity. arXiv:2202.01412 [math.MG].
- ↑ Nadis, Steve. An Ancient Geometry Problem Falls to New Mathematical Techniques (англ.). Quanta Magazine (8 февраля 2022). Дата обращения: 18 февраля 2022. Архивировано 18 февраля 2022 года.
Ссылки
- Hertel, Eike; Richter, Christian (2003), Squaring the circle by dissection (PDF), Beiträge zur Algebra und Geometrie, 44 (1): 47–55, MR 1990983 Архивная копия от 3 марта 2016 на Wayback Machine.
- Laczkovich, Miklós (1990), Equidecomposability and discrepancy: a solution to Tarski's circle squaring problem, Journal für die Reine und Angewandte Mathematik, 404: 77–117, doi:10.1515/crll.1990.404.77, MR 1037431
{{citation}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка). - Laczkovich, Miklós (1994), Paradoxical decompositions: a survey of recent results, Proc. First European Congress of Mathematics, Vol. II (Paris, 1992), Progress in Mathematics, vol. 120, Basel: Birkhäuser, pp. 159–184, MR 1341843
{{citation}}: Википедия:Обслуживание CS1 (множественные имена: authors list) (ссылка). - Tarski, Alfred (1925), Probléme 38, Fundamenta Mathematicae, 7: 381.
- Wilson, Trevor M. (2005), A continuous movement version of the Banach–Tarski paradox: A solution to De Groot's problem, Journal of Symbolic Logic, 70 (3): 946–952, doi:10.2178/jsl/1122038921, MR 2155273.