Колчан (математика)

Колчан (математика) — ориентированный граф, где разрешены петли и кратные рёбра.^[1] Колчаны обычно используются в теории представлений.^[2] Представление колчана сопоставляет каждой вершине колчана векторное пространство V(x) и каждому ребру a линейное отображение V(a).^[3]

Колчан Г состоит из:

• Множества V вершин Г
• Множества E ребер Г
• Двух функций: s:E \to V, задающей «начало» ребра, и ещё одной функции, t:E \to V, задающей «конец» ребра.

Это определение идентично определению мультиграфа.

Морфизм колчанов — это отображение вершин в вершины, которое переводит направленные ребра в направленные ребра. Обозначим два колчана как ${\displaystyle \Gamma =(V,E,s,t)}$ и ${\displaystyle \Gamma '=(V',E',s',t')}$. Тогда морфизм ${\displaystyle m=(m_{v},m_{e})}$ этих колчанов состоит из двух функций ${\displaystyle m_{v}:V\to V'}$ и ${\displaystyle m_{e}:E\to E'}$ таких, что следующие диаграммы коммутируют:

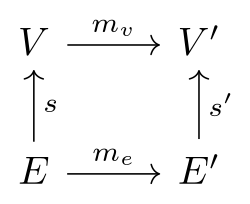
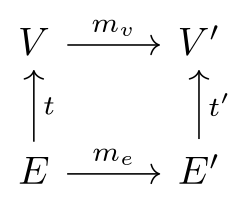
То есть,

${\displaystyle m_{v}\circ s=s'\circ m_{e}}$

и

${\displaystyle m_{v}\circ t=t'\circ m_{e}}$

Колчан имеет конечный тип, если он имеет только конечное число классов изоморфизма неразложимых представлений. Gabriel (1972) классифицировал все колчаны конечного типа, а также их неразложимые представления. Теорема Габриэля утверждает, что^[4]

1. (Связный) колчан имеет конечный тип тогда и только тогда, когда его базовый граф (когда направления стрелок игнорируются) является одной из диаграмм Дынкина по классификации ADE: A_n, D_n, E₆, E₇, E₈.
2. Неразложимые представления находятся во взаимно-однозначном соответствии с положительными корнями системы корней диаграммы Дынкина.

• ADE-классификация
• Групповое кольцо
• Торическое многообразие

• Derksen, Harm; Weyman, Jerzy (February 2005), Quiver Representations (PDF), Notices of the American Mathematical Society, 52 (2)
• Dlab, Vlastimil; Ringel, Claus Michael (1973), On algebras of finite representation type, Carleton Mathematical Lecture Notes, vol. 2, Department of Mathematics, Carleton Univ., Ottawa, Ont., MR 0347907
• Crawley-Boevey, William (1992), Notes on Quiver Representations (PDF), Oxford University, Архивировано из оригинала (PDF) 24 июля 2011, Дата обращения: 17 февраля 2007
• Gabriel, Peter (1972), Unzerlegbare Darstellungen. I, Manuscripta Mathematica, 6 (1): 71–103, doi:10.1007/BF01298413, ISSN 0025-2611, MR 0332887.
• Victor Kac, "Root systems, representations of quivers and invariant theory". Invariant theory (Montecatini, 1982), pp. 74–108, Lecture Notes in Math. 996, Springer-Verlag, Berlin 1983. ISBN 3-540-12319-9^[1]
• King, Alastair (1994), Moduli of representations of finite-dimensional algebras, Quart. J. Math., 45 (180): 515–530, doi:10.1093/qmath/45.4.515
• Savage, Alistair (2006) [2005], Finite-dimensional algebras and quivers, in Francoise, J.-P.; Naber, G. L.; Tsou, S.T. (eds.), Encyclopedia of Mathematical Physics, vol. 2, Elsevier, pp. 313–320, arXiv:math/0505082, Bibcode:2005math......5082S
• Simson, Daniel; Skowronski, Andrzej; Assem, Ibrahim (2007), Elements of the Representation Theory of Associative Algebras, Cambridge University Press, ISBN 978-0-521-88218-7
• И. Н. Бернштейн, И. М. Гельфанд, В. А. Пономарев, Функторы Кокстера и теорема Габриеля, УМН, 28:2(170) (1973), 19–33; Russian Math. Surveys, 28:2 (1973), 17–32.

1. ↑ Invariant theory: proceedings of the 1st 1982 Session of the Centro Internazionale Matematico Estivo (C.I.M.E.), held at Montecatini, Italy, June 10-18, 1982. — Berlin Heidelberg : Springer, 1983. — ISBN 978-3-540-12319-4.