Лемма о ромбе

Лемма о ромбе (или лемма Ньюмана) даёт простой способ проверить сходимость переписывающей системы без убывающих бесконечных цепей. Доказана Максом Ньюманом в 1942 году. Стандартное доказательство использует нётерову индукцию.

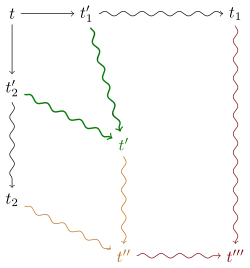
Пусть ${\displaystyle A}$ — переписыващая система, то есть есть орграф. Наличие ребра из вершины ${\displaystyle x}$ в вершину ${\displaystyle y}$ будет обозначаться ${\displaystyle x\to y}$. Наличие направленного пути из ${\displaystyle x}$ в ${\displaystyle y}$ (включая путь нулевой длины) будет обозначаться ${\displaystyle x\rightsquigarrow y}$.

Предположим, что ${\displaystyle A}$

• нётерова, то есть не существует бесконечной цепи ${\displaystyle x_{0}\to x_{1}\to \dots }$
• локально конфлюентна, то есть если ${\displaystyle x\to y}$ и ${\displaystyle x\to z}$ то ${\displaystyle y\rightsquigarrow w}$ и ${\displaystyle z\rightsquigarrow w}$ для некоторого ${\displaystyle w}$.

Тогда система ${\displaystyle A}$ конфлюентна; то есть если ${\displaystyle x\rightsquigarrow y}$ и ${\displaystyle x\rightsquigarrow z}$ то ${\displaystyle y\rightsquigarrow w}$ и ${\displaystyle z\rightsquigarrow w}$ для некоторого ${\displaystyle w}$.

• M. H. A. Newman. On theories with a combinatorial definition of "equivalence". Annals of Mathematics, 43, Number 2, pages 223–243, 1942.
• Paterson, Michael S. Automata, languages, and programming: 17th international colloquium. — Warwick University, England : Springer, 1990. — Vol. 443. — ISBN 978-3-540-52826-5.
• Term Rewriting Systems, Terese, Cambridge Tracts in Theoretical Computer Science, 2003. (book weblink)
• Term Rewriting and All That, Franz Baader and Tobias Nipkow, Cambridge University Press, 1998 (book weblink)
• John Harrison, Handbook of Practical Logic and Automated Reasoning, Cambridge University Press, 2009, ISBN 978-0-521-89957-4, chapter 4 "Equality".

• Виктор Губа «Переписывающие системы»