Подерная система координат

Поде́рная систе́ма координа́т — система координат, основанная на подерном преобразовании. Подерные координаты точки дифференцируемой кривой состоят из двух величин, двух расстояний от некоторой заданной точки (полюса): до точки кривой и до соответствующей точки её подеры^[1]^[2].

Традиционные системы координат, такие, как декартова и полярная, суть точечные понятия. В этих системах для любой точки плоскости один и только один набор координат с традиционными обозначениями $(x,\;y)$ для декартовой и $(r,\;\varphi )$ для полярной системы. В противоположность этому подерные координаты зависят от конкретных кривых, и произвольная точка плоскости имеет много разных подерных координат $(r,\;p)$ , которые зависят от выбранной кривой и полюса^[1].

Определение подерных координат

Поде́рные координа́ты данной точки плоскости относительно произвольной фиксированной точки и дифференцируемой кривой, проходящей через данную точку, — расстояние $r$ от фиксированной точки до данной точки и расстояние $p$ от фиксированной точки до касательной к кривой в данной точке. Другими словами, подерные координаты точки кривой состоят из двух величин, двух расстояний от фиксированной точки: $r$ до точки кривой и $p$ до соответствующей точки её подеры^[3].

Фиксированная точка из определения подерных координат называется началом координат, или подерной точкой, или полюсом подерной системы счисления, расстояние $r$ от начала координат до точки на кривой называется радиальным расстоянием точки кривой, а расстояние $p$ от начала координат до касательной прямой — перпендикулярным расстоянием точки кривой^[3].

Если, например, взять другую кривую, проходящую через данную точку, оставив начало координат на месте, то в этом случае значение радиального расстояния $r$ останется прежним, но перпендикулярное расстояние $p$ может быть другим. Кроме того, изолированная точка кривой не имеет второй координаты $p$ , а точка самопересечения имеет две разные координаты $p$ ^[4].

Пропорциональность подерных координат

Имеет место следующее утверждение о пропорциональности подерных координат:

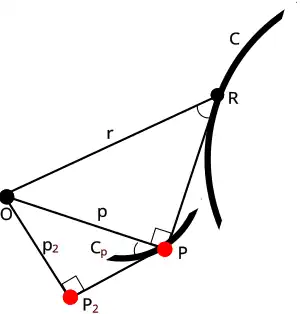
радиальные и перпендикулярные расстояния кривой

C

и её подеры

C_{P}

относительно полюса

O

пропорциональны, то есть

{\frac {p}{r}}={\frac {p_{2}}{p}},

или

p^{2}=rp_{2},

или

p_{2}={\frac {p^{2}}{r}}=\left({\frac {p}{r}}\right)^{2}r,

где:

r

— радиальное расстояние текущей точки

R

исходной кривой от полюса

O;

p

— перпендикулярные расстояние точки исходной кривой

R

от полюса

O,

оно же радиальное расстояние соответствующей точки первой подеры

P

от полюса

O;

p_{2}

— перпендикулярное расстояние соответствующей точки первой подеры

P

от полюса

O,

оно же радиальное расстояние соответствующей точки второй подеры

P_{2}

от полюса

O

, как показано на рисунке справа^[5]^[6].

Доказательство^[7]

Комплексное уравнение подеры относительно полюса $\mathbf {z} _{0}=(0,\;i0)$ в её текущей точке $P$ имеет вид

p(t)={\frac {z(t){\overline {z'(t)}}-{\overline {z(t)}}z'(t)}{2{\overline {z'(t)}}}}.

Дифференцируя это уравнение, получим касательную подеры в этой точке:

p'(t)={\frac {z(t){\overline {z''(t)}}-{\overline {z(t)}}z''(t)}{2{\overline {z'(t)}}}}-{\frac {z(t){\overline {z'(t)}}-{\overline {z(t)}}z'(t)}{2{\overline {z'(t)}}^{2}}}{\overline {z''(t)}},

p'(t)={\frac {z'(t){\overline {z''(t)}}-{\overline {z'(t)}}z''(t)}{2{\overline {z'(t)}}^{2}}}{\overline {z(t)}}.

Разделим обе части этого уравнения на $p(t),$ получим:

{\frac {p'(t)}{p(t)}}={\frac {z'(t){\overline {z''(t)}}-{\overline {z'(t)}}z''(t)}{2{\overline {z'(t)}}^{2}p(t)}}{\overline {z(t)}},

{\frac {p'(t)}{p(t)}}={\frac {z'(t){\overline {z''(t)}}-{\overline {z'(t)}}z''(t)}{z(t){\overline {z'(t)}}-{\overline {z(t)}}z'(t)}}{\frac {\overline {z(t)}}{\overline {z'(t)}}}.

Поскольку выражение для любых двух комплексных чисел $z_{1}=a_{1}+b_{1}i$ и $z_{2}=a_{2}+b_{2}i$

z_{1}{\bar {z}}_{2}-{\bar {z}}_{1}z_{2}=(a_{1}+b_{1}i)(a_{2}-b_{2}i)-(a_{1}-b_{1}i)(a_{2}-b_{2}i)=

{}=b_{1}a_{2}i-a_{1}b_{2}i+b_{1}a_{2}i-a_{1}b_{2}i=2(b_{1}a_{2}-a_{1}b_{2})i

есть чисто мнимое число, то первый множитель правой части этого уравнения есть вещественное число,

Поэтому аргументы комплексных чисел

\operatorname {Arg} {\frac {p'(t)}{p(t)}}=\operatorname {Arg} {\frac {\overline {z(t)}}{\overline {z'(t)}}}=\operatorname {Arg} {\frac {z'(t)}{z(t)}}.

Следовательно, равны следующие два угла:

угол между отрезком $OR$ и касательной $RP$ к исходной кривой $C$ в точке $R;$
угол между отрезком $OP$ и касательной $PP_{2}$ к подере $C_{P}$ в точке $P.$

Отсюда следует, что подобны два прямоугольных треугольника $\triangle ORP$ и $\triangle OPP_{2},$ так как у них равны острые углы $\angle ORP$ и $\angle OPP_{2}.$

Другими словами,

{\frac {p}{r}}={\frac {p_{2}}{p}}.

Для третьей подеры получаем следующее радиальное расстояние^[6]:

p_{3}=\left({\frac {p_{2}}{p}}\right)^{2}p=\left({\frac {p^{2}}{rp}}\right)^{2}p=\left({\frac {p}{r}}\right)^{3}r,

и аналогично для $n$ -й подеры имеем общую формулу радиального расстояния

p_{n}=\left({\frac {p}{r}}\right)^{n}r.

Для антиподеры $p_{-1}$ изменим в пропорции обозначения^[6]:

{\frac {r}{p_{-1}}}={\frac {p}{r}},

откуда

p_{-1}={\frac {r^{2}}{p}}=\left({\frac {p}{r}}\right)^{-1}r,

для второй антиподеры

p_{-2}=\left({\frac {p_{-1}^{2}}{r}}\right)=\left({\frac {r^{3}}{p^{2}}}\right)=\left({\frac {p}{r}}\right)^{-2}r,

и аналогично для $n$ -й антиподеры имеем общую формулу радиального расстояния

p_{-n}=\left({\frac {p}{r}}\right)^{-n}r.

Также

p_{-n}=\left({\frac {r}{p_{-1}}}\right)^{-n}r,\quad

p_{n}=\left({\frac {r}{p_{-1}}}\right)^{n}r.

Примеры подерных уравнений кривых

В этом разделе собраны примеры подерных уравнений кривых, то есть уравнений в подерной системе координат. Параметр $a$ задаёт размеры кривой^[8]:

Астроида

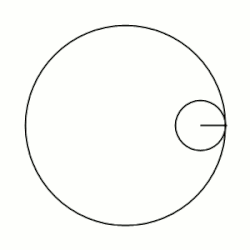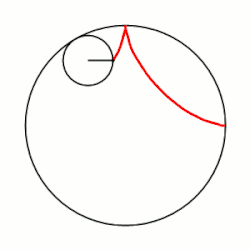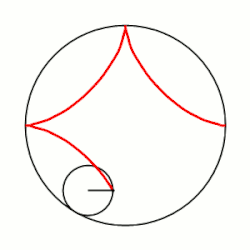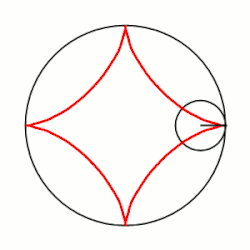Полюс подерных координат: центр астроиды.

Параметр

a

: радиус окружности, в которую вписана астроида.

Подерное уравнение:

r^{2}+3p^{2}=a^{2}.

Лемниската Бернулли

Полюс подерных координат: центр лемнискаты.

Параметр

a

: радиус окружности, в которую вписана лемниската.

Подерное уравнение:

pa^{2}=r^{3}.

Окружность

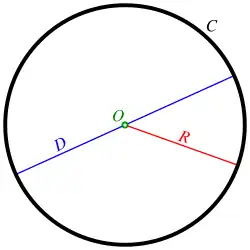Полюс подерных координат: центр окружности.

Параметр

a

: радиус окружности.

Подерное уравнение:

pa=r^{2}.

Парабола

Полюс подерных координат: фокус параболы.

Параметр

a

: расстояние от фокуса до вершины параболы.

Подерное уравнение:

p^{2}=ar.

Эллипс

Полюс подерных координат: фокус эллипса.

Параметры

a

и

b

: большая и малая полуоси эллипса.

Подерное уравнение:

{\frac {b^{2}}{p^{2}}}={\frac {2a}{r}}-1.

Примечания

1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2.
↑ Брус Дж., Джиблин П. Кривые и особенности, 1988, 7.21. Упражнения. 6, с. 176—177.
1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2—3.
↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 3.
↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 48.
1 2 3 Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 152.
↑ Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 151—152.
↑ Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 4.

Источники

Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей: Пер. с англ. И. Г. Щербак под ред. В. И. Арнольда. М.: Мир, 1988. 262 с, ил. (Современная математика. Вводные курсы) ISBN 5-03-001194-3. [J. William Bruce, Peter G. Giblin. Curves and Singularities. A geometrical introduction to singularity theory. Cambridge: Cambridge University Press, 1984.]
Lawrence J. D. A Catalog of Special Plane Curves. New York: Dover Publications, Inc., 1972. 218 p.
Zwikker C. The Advanced Geometry of Plane Curves and Their ApplicationsThe Advanced Geometry of Plane Curves and Their Applications. New York: Dover Publications, Inc., 1963. 299 p. ISBN 0486610780. ISBN 9780486610788.

[_869cddd5317c52f3-1] 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2.

[_7995f2916862cebf-2] Брус Дж., Джиблин П. Кривые и особенности, 1988, 7.21. Упражнения. 6, с. 176—177.

[_7de8534ad9624878-3] 1 2 Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 2—3.

[_7c32cad52b17320c-4] Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 3.

[_721c9e0f5b6b5627-5] Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 48.

[_15611ed71f5be077-6] 1 2 3 Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 152.

[_6421757f6ab8d724-7] Zwikker C. The Advanced Geometry of Plane Curves and Their Applications, 1963, Chapter XI. Pedals and other derived curves, p. 151—152.

[_544963d5157262d5-8] Lawrence J. D. A Catalog of Special Plane Curves, 1972, 1.1. Coordinate Systems, p. 4.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]