Полукруговой закон Вигнера
| Полукруговое распределение | |
|---|---|
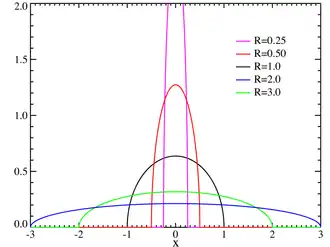 Плотность вероятности Плотность вероятности | |
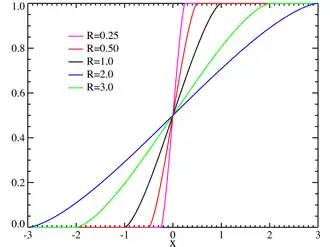 Функция распределения Функция распределения | |
| Параметры | радиус (вещественное положительное число) |
| Носитель | |
| Плотность вероятности | |
| Функция распределения |
для |
| Математическое ожидание | |
| Медиана | |
| Мода | |
| Дисперсия | |
| Коэффициент асимметрии | |
| Коэффициент эксцесса | |
| Дифференциальная энтропия | |
| Производящая функция моментов | |
| Характеристическая функция | |
Полукруговой закон (или распределение) Вигнера — названное в честь физика Юджина Вигнера абсолютно непрерывное распределение вероятностей на прямой, график плотности которого получается после нормировки из полукруга, построенном на отрезке [-R,R] как на диаметре (тем самым, на самом деле график плотности оказывается полуэллипсом):
если , и иначе.
Это распределение было предложено Вигнером в 1955 году в связи с его исследованиями в области квантовой механики, как предельное распределение собственных значений для случайной эрмитовой матрицы большого размера.
Литература
- Weisstein, Eric W. Wigner's Semicircle Law (англ.) на сайте Wolfram MathWorld.
- Wigner Е. Characteristic vectors of bordered matrices with infinite dimensions. Ann. of Math., 62 (1955), 548-564.
- Wigner E. On the distribution of the roots of certain symmetric matrices. Ann. of Math., 67 (1958), 325-328.
- Синай Я. Г., Сошников А. Б. Уточнение полукругового закона Вигнера в окрестности края спектра для случайных симметричных матриц. Функциональный анализ и его приложения, 1998. — Том 32. Выпуск 2. — С. 56—79.