Полоса (математика)

Полоса́^[1] (синоним — поло́ска^[2]) — множество всех точек, которые находятся между двумя параллельными прямыми плоскости^[3][4][5]. Эти две прямые ограничивают полосу, и расстояние между ними называется шириной полосы^[1][6][2].

Полоса является выпуклой областью^[7], а также частным случаем трубчатой области^[8].

В общем двумерном случае на плоскости ${\displaystyle \mathbb {R} ^{2}}$ с координатами ${\displaystyle (x,\,y)}$ координаты точек плоской полосы отвечают следующим неравенствам, использующим общее уравнение прямой:

${\displaystyle C_{1}<Ax+By<C_{2}}$,

где ${\displaystyle A,\,B,\,C_{1},\,C_{2}}$ — постоянные, причём ${\displaystyle A}$ и ${\displaystyle B}$ одновременно не равны нулю^[3][4][5].

В литературе подобные неравенства часто также пишут в нестрогом виде^[9][10][11]:

${\displaystyle C_{1}\leqslant Ax+By\leqslant C_{2}}$,

Полосу можно также определить, задав уравнения прямых, которые её ограничивают, или даже указав направление этих прямых, точку на плоскости на середине полосы и её ширину^[2].

Обычно система координат подбирается таким образом, чтобы прямые, которые ограничивают полосу, были параллельны одной из осей координат^[6][2].

Горизонтальная полоса^[1], или полоса, параллельная оси абсцисс — полоса, ограничивающие прямые которой параллельны горизонтальной оси абсцисс^[2][12].

Вертикальная полоса^[1], или полоса, параллельная оси ординат — полоса, ограничивающие прямые которой параллельны вертикальной оси ординат^[2][12].

При использовании горизонтальных и вертикальных полос неравенство полосы упрощается. Горизонтальную полосу можно задавать следующими неравенствами^{[9][10][13][11][14]}:

${\displaystyle C_{1}<y<C_{2}}$, ${\displaystyle \quad C_{1}\leqslant y\leqslant C_{2}}$, ${\displaystyle \quad |y|<C}$, ${\displaystyle \quad |y|\leqslant C}$,

а вертикальную полосу — следующими неравенствами:

${\displaystyle C_{1}<x<C_{2}}$, ${\displaystyle \quad C_{1}\leqslant x\leqslant C_{2}}$, ${\displaystyle \quad |x|<C}$, ${\displaystyle \quad |x|\leqslant C}$.

На комплексной плоскости ${\displaystyle \mathbb {C} }$ с координатами ${\displaystyle z=x+iy}$ конформное преобразование ${\displaystyle w=e^{z}}$ отображает полосу ${\displaystyle 0<y<\pi }$ на верхнюю полуплоскость^{[3][4][5][15]}, а полосу ${\displaystyle 0<y<2\pi }$ — на всю плоскость без положительной полуоси ${\displaystyle \{x>0,\,y=0\}}$^[16]. Однолистное и конформное преобразование ${\displaystyle w=\operatorname {tg} z}$ отображает полосу ${\displaystyle -{\frac {\pi }{4}}<x<{\frac {\pi }{4}}}$ на внутренность единичного круга^[17].

Полуполоса — любая из двух областей, на которые разбивает полосу прямая, её пересекающая. Например, вертикальную полуполосу можно задать следующими неравенствами^[18]:

${\displaystyle C_{1}<x<C_{2},\,y>0.}$

На комплексной плоскости ${\displaystyle \mathbb {C} }$ с координатами ${\displaystyle z=x+iy}$ однолистное и конформное преобразование ${\displaystyle w=\sin z}$ отображает полуполосу ${\displaystyle -{\frac {\pi }{2}}<x<{\frac {\pi }{2}},\,y>0}$ на верхнюю полуплоскость. На рисунке внизу показано соответствие линий при этом преобразовании, а именно^[19]:

• вертикальные лучи ${\displaystyle \{x=x_{0},\,0<y<\infty \}}$ отображаются на верхнюю полуплоскость в части гипербол с фокусами ${\displaystyle \pm 1}$;
• горизонтальные отрезки ${\displaystyle \{-{\frac {\pi }{2}}<x<{\frac {\pi }{2}},\,y=y_{0}\}}$ отображаются на верхнюю полуплоскость в части эллипсов с теми же фокусами ${\displaystyle \pm 1}$.

• Преобразование полуполосы в полуплоскость
• 
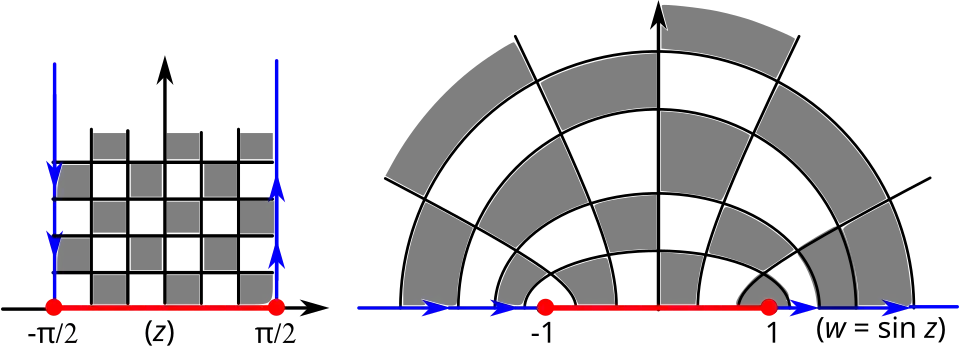  Преобразование вертикальной полуполосы в верхнюю полуплоскость функцией ${\displaystyle w=\sin z}$

Пространственная полоса — в случае трёхмерного пространства множество всех точек, которые находятся между двумя параллельными плоскостями пространства^{[20][21][3][4][5]}. Эти две плоскости ограничивают полосу, и расстояние между ними называется шириной полосы^[1][6][2].

В пространстве ${\displaystyle \mathbb {R} ^{n}}$ систему координат ${\displaystyle (x_{1},\,x_{2},\,\dots ,\,x_{n})}$ можно подобрать таким образом, что координаты точек пространственной ${\displaystyle n}$-мерной полосы будут задаваться следующими неравенствами:

${\displaystyle C_{1}<x_{1}<C_{2}}$,

где ${\displaystyle C_{1},\,C_{2}}$ — постоянные^{[20][3][4][5]}.

• Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
• Бляшке В. Круг и шар: Пер. с нем. В. А. Залгаллера и С. И. Залгаллер под ред. В. А. Залгаллера и И. М. Яглома. М.: «Наука», 1967. 232 с., ил. [Wilhelm Blaschke. Kreis und Kugel: 2., durchgesehene und verbesserte Auflage. Berlin: Walter de Oruyter & Co vormals G. J. Göschen'sche Verlagshandlung (J. Guttentag, Verlagsbuchhandlung Georg Relmer Karl J. Trübner) Velt & Соmр. 1936.]
• Брус Дж., Джиблин П. Кривые и особенности: Геометрическое введение в теорию особенностей: Пер. с англ. И. Г. Щербак под ред. В. И. Арнольда. М.: Мир, 1988. 262 с. (Современная математика. Вводные курсы) ISBN 5-03-001194-3. [J. William Bruce, Peter G. Giblin. Curves and Singularities. A geometrical introduction to singularity theory. Cambridge: Cambridge University Press, 1984.]
• Владимиров В. С. Методы теории функций многих комплексных переменных / Предисловие академика Н. Н. Боголюбова. М.: «Наука», 1964. 411 с.: ил.
• Клейн Ф. Высшая геометрия: Пер. с нем. Н. К. Брушлинского. Изд. 2-е, стереотипное. М.: Едиториал УРСС, 2004. 399 с., ил. ISBN 5-354-00603-1. [Felix Klein. Vorlesungen über höhere Geometrie.]
• Коллатц Л. Функциональный анализ и вычислительная математика: Пер. с нем. И. Г. Нидеккер под ред. А. Д. Горбунова. М.: «Мир», 1969. 447 с., ил. [Lothar Collatz. Funktionalanalysis und numerische Mathematik. Berlin·Göttingen·Heidelberg: Springer-Verlag, 1964.]
• Курант Р., Роббинс Г. Что такое математика? Элементарный очерк идей и методов: Пер. с англ. под ред. А. Н. Колмогорова. Изд. 7-e, стереотипное. М.: МЦНМО, 2015. 564 с., ил. ISBN 978-5-4439-0628-7. [Richard Courant, Herbert Robbins. What Is Mathematics? An Elementary Approach to Ideas and Methods. London·New York·Toronto: Oxford University Press.]
• Полоса // Большая советская энциклопедия. (В 30 томах) Гл. ред. А. М. Прохоров. Изд. 3-е. М.: «Советская энциклопедия», 1975. Т. 20. Плата — проб. 1975. 608 с. С. 249.
• Полоса // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская энциклопедия», 1984. 1216 стб. Стб. 437.
• Полоса // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 473.
• Стоилов С. Лекции о топологических принципах теории аналитических функций: Пер. с фр. Е. И. Стечкиной под ред. Б. В. Шабата. М.: «Наука», 1964. 227 с., ил. [Stoïlow S. Leçons sur les principes topologiques de la théorie des fonctions analytiques. Paris, 1956.]
• Шабат Б. В. Введение в комплексный анализ, ч. 1, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 320 с.: ил.
• Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.