Приближение малых углов

Приближение малых углов — математический приём, позволяющий вычислять тригонометрические функции для малых углов по следующим приближённым формулам:

{\begin{aligned}\sin \theta &\approx \tan \theta \approx \theta ,\\[5mu]\cos \theta &\approx 1-{\tfrac {1}{2}}\theta ^{2}\approx 1,\end{aligned}}

если угол $\theta$ выражен в радианах.

Приближение широко используется в фундаментальных и прикладных технических науках, в том числе механике, оптике, астрономии. Одним из важных применений приближения является упрощение вида дифференциальных уравнений для случаев малых отклонений вблизи положения равновесия.

Обоснования применимости

Геометрическое

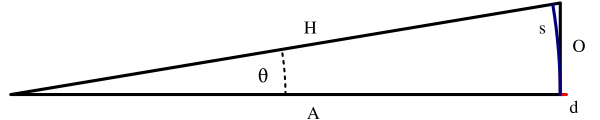
Прямоугольный треугольник с малым острым углом

Для прямоугольного треугольника с малым острым углом $\theta$ длина прилежащего катета $A$ приблизительно равна длине гипотенузы $H$ , а противолежащий катет $O$ примерно равен по длине дуге $S$ окружности с радиусом, равным гипотенузе. Тогда

{\begin{aligned}\cos \theta ={\frac {A}{H}}&\approx {\frac {H}{H}}=1,\\[5mu]\tan \theta ={\frac {O}{A}}&\approx {\frac {O}{H}}=\sin \theta \approx {\frac {S}{H}}={\frac {\theta \cdot H}{H}}=\theta \end{aligned}}