Список картографических проекций
В этом списке картографические проекции рассортированы по виду поверхности проектирования. Традиционно выделяют три категории проекций: цилиндрические, конические и азимутальные. Некоторые проекции трудно отнести к какой-либо из этих трёх категорий. С другой стороны, проекции можно классифицировать по характеристикам поверхности, которые они оставляют неизменными: направления, локальную форму, площадь и расстояние.
Таблица проекций
Цилиндрические
Термин «цилиндрическая проекция» используются по отношению к любой проекции, для которой меридианы проецируются в равноотстоящие вертикальные линии, а параллели — в горизонтальные линии.
| Проекция | Пример | Создатель | Год | Примечания |
|---|---|---|---|---|
| Равнопромежуточная проекция | 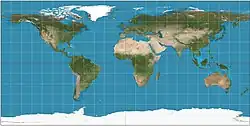 |
Марин Тирский | ок. 120 г. н. э. | Простая геометрия; сохраняет расстояния вдоль экватора и всех меридианов |
| Галла — Петерса | 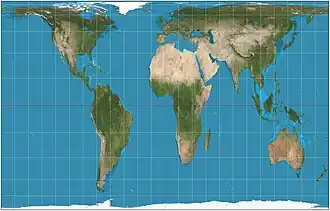 |
Джеймс Галл, | 1855 | Равновеликая |
| Равновеликая цилиндрическая проекция Ламберта | Иоганн Ламберт | 1772 | Равновеликая | |
| Проекция Меркатора | 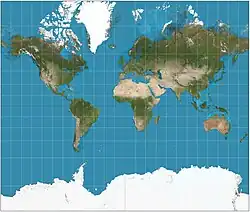 |
Герард Меркатор | 1569 | Сохраняет углы, не может отображать полюса |
| Цилиндрическая проекция Миллера | 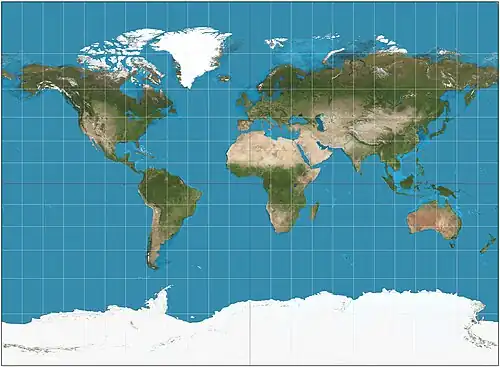 |
Осборн Миллер | 1942 | Отображает полюса |
| Центральная цилиндрическая проекция | XIX в. | Используется в панорамной фотографии |
Псевдоцилиндрические
Псевдоцилиндрические проекции представляют центральный меридиан и все параллели в виде отрезков прямых, проекции прочих меридианов не являются прямыми[1].
| Проекция | Пример | Создатель | Год | Примечания |
|---|---|---|---|---|
| Проекция Эккерта IV | 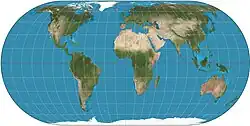 |
Макс Эккерт-Грейфендорфф | ||
| Проекция Эккерта VI | 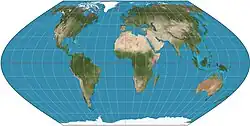 |
Макс Эккерт-Грейфендорфф | ||
| Проекция Гуда | 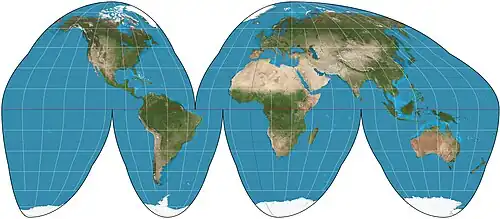 |
Джон Гуд | 1923 | |
| Проекция Каврайского | 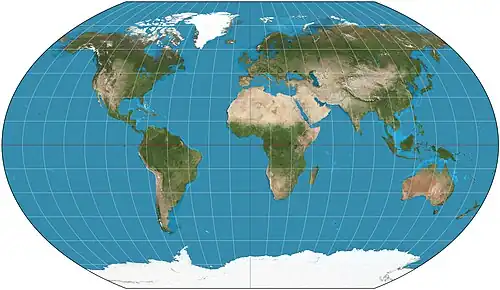 |
В. В. Каврайский | 1939 | |
| Проекция Мольвейде | 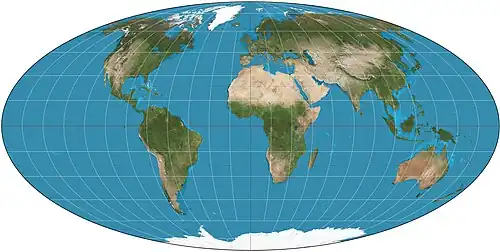 |
Карл Моллвейде | 1805 | |
| Синусоидальная проекция | 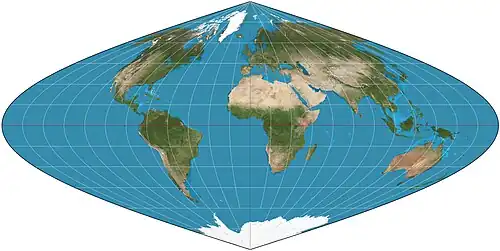 |
Николя Сансон | ||
| Гиперэллиптическая проекция Тоблера | 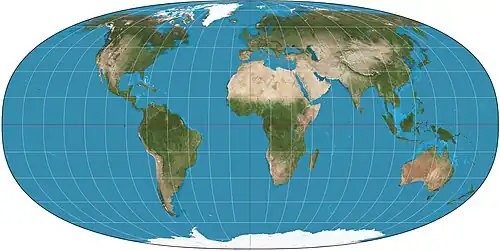 |
Валдо Тоблер | 1973 | |
| Проекция Вагнера | 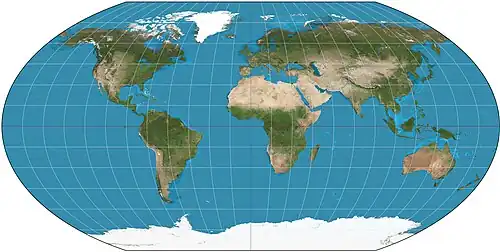 |
К. Х. Вагнер | ||
| Проекция Хёльцеля | 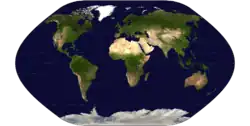 |
Хельцель | Ок. 1960 |
Конические
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Равнопромежуточная | Птолемей | ||
| Равноугольная Ламберта | 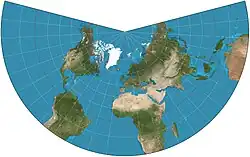 |
Иоганн Ламберт |
Псевдоконические
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Проекция Бонне | 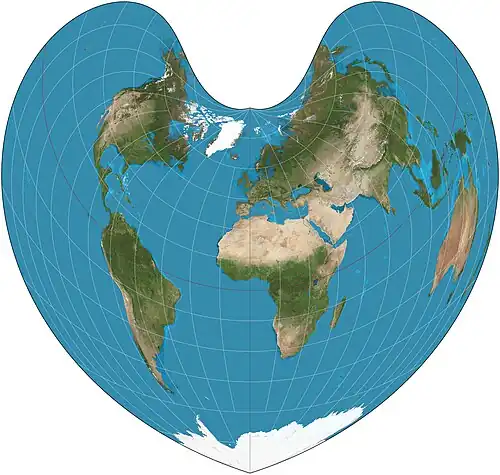 |
Ригобер Бонне | |
| Проекция Вернера | 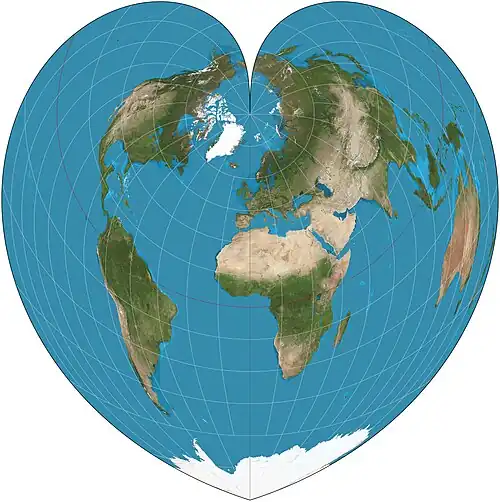 |
Иоганнес Вернер, Иоганнес Стабиус |
|
| Поликоническая | 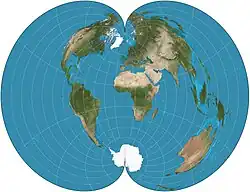 |
Фердинанд Хасслер |
Азимутальные
Азимутальные проекции сохраняют направления из центральной точки (и следовательно, большие окружности, проходящие через центральную точку, представлены прямыми на карте). Как правило, такие проекции также имеют радиальную симметрию масштабов, а значит и искажений: расстояния на карте из центральной точки вычисляются по функции r(d) от истинного расстояния d, независимо от угла; соответственно, круги с центром в центральной точке представлены кругами с центром в центральной точке на карте.
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Азимутальная проекция | 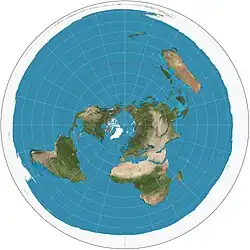 |
Эта проекция используется Геологической службой США в Национальном Атласе США, а также в эмблеме ООН. | |
| Равновеликая азимутальная проекция Ламберта | 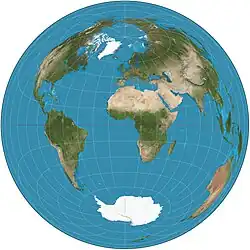 |
Иоганн Ламберт |
Псевдоазимутальные
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Аитова | 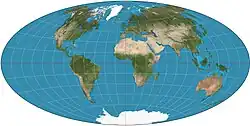 |
Давид Аитов | |
| Хаммера | 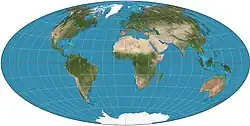 |
Эрнст Хаммер | |
| Тройная Винкеля | 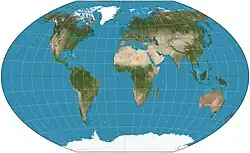 |
Освальд Винкель |
Полиэдрические
Полиэдрические проекции проецируют поверхность геоида на различные многогранные аппроксимации сферы. В качестве проекции на каждую грань часто используется гномоническая проекция, но некоторые картографы предпочитают равновеликую проекцию Фишера-Снайдера или равноугольную проекцию[2].
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| «Бабочка» Кахилла | 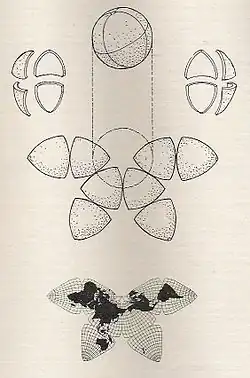 |
Бернард Кэххил | |
| «Бабочка» Уотермана | 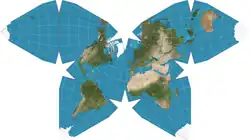 |
Стив Уотерман | |
| Квадрилатеральный сферический куб | Ф. Кеннетт Чан, Э. М. О`Нил | Равновеликая | |
| Проекция Пирса | 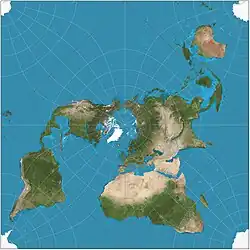 |
Чарлз Пирс | Равноугольная |
| Проекция Димаксион | 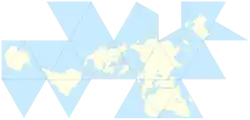 |
Бакминстер Фуллер | Уменьшение искажений ценой нарушения непрерывности карты |
| Мириаэдрическая проекция | Джек Ван Вийк | Проекция глобуса на так называемый «мириаэдр» — многогранник с несколькими тысячами граней.[3][4] |
Проекции по их метрическим свойствам
Равноугольные
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Равноугольная коническая проекция Ламберта |  |
Иоганн Ламберт | Не отображает южный полюс |
| Проекция Меркатора |  |
Герард Меркатор | Не отображает полюса |
| Проекция Пирса |  |
Чарльз Пирс | Равноугольная |
Равновеликие
- Проекция Моллвейде (эллиптическая)
- Проекция Бонне и проекция Боттомли, их частными случаями являются:
- Синусоидальная проекция
- Проекция Вернера (кардиоидная)
- Проекция Колиньона
- cylindrical equal-area, семейство проекций, включающее:
- Проекция Галла — Петерса
- Равновеликая цилиндрическая проекция Ламберта
- Проекция Берманна
- Равноплощадная проекция Смита, или прямоугольная проекция Краснера
- Тристан Эдвардс
- Проекция Хобо — Дайера
- Балтасарт
- Проекция Альберса
- Равноплощадная азимутная проекция Ламберта
- Проекция Хаммера
- Briesemeister
- Гиперэллиптическая проекция Тоблера, семейство проекций, включающее особый случай проекции Мольвельде, Колиньона и других цилиндрических равновеликих проекций.
- квадрилатеральный сферический куб
- Равновеликая полиэдрическая проекция Снайдера, используемая для геодезических решёток.
Гибридные карты, использующие в одних регионах одну равновеликую проекции, а в других — другую:
- HEALPix: Равновеликие цилиндрические проекции Колиньона и Ламберта;
- Гомолосинусоидальная проекция Гуда: синусоидальная + Мольвельде;
- Philbrick Sinu-Mollweide: синусоидальная + Мольвельде, косая, ненепрерваная[5].
- Асимметричная проекция Хатано: две разные псевдоцилиндрические проекции равной площади соединяются на Экваторе.
Многогранные равноплощадые карты обычно используют равновеликую проекция Ирвинга Фишера, в то время как большинство многогранных равноплощадых карт используют гномоническую прокцию.[6]
Равнопромежуточные
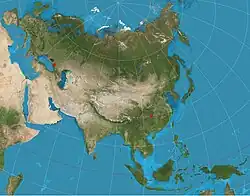
Равнопромежуточные проекции сохраняют расстояние между некоторыми стандартными точками или линиями.
- Азимутная равнопромежуточная проекция — сохраняет расстояния вдоль больших окружностей, исходящих из центра
- Равнопромежуточная проекция — сохраняет расстояния вдоль меридиан[уточнить]
- Проекция плате-карре — равнопромежуточная проекция с центром на экваторе
- Проекция Кассини (в честь Кассини, Цезарь Франсуа, иногда проекция Кассини — Зольднера) — поперечная цилиндрическая проекция сохраняет масштаб вдоль центрального меридиана и всех линий, параллельных ему, и не является ни равновеликой, ни равноугольной[7].
- Равнопромежуточная коническая проекция — локальные формы являются истинными вдоль стандартных параллелей, искажение постоянно вдоль любой данной параллели, но увеличивается по мере удаления от стандартных параллелей[8][9].
- Проекция Вернера, сохраняющая расстояние до северного полюса и по кривой вдоль параллелей;
- Равнопромежуточная проекция двух точек: две «контрольные точки» выбираются произвольно составителем карты. Сохраняются расстояния между любой точкой на карте и этими точками[10].
- Ортографическая проекция — сохраняет расстояния между параллелями[11]
- Синусоидная проекция — сохраняет расстояния между параллелями
- Азимутальная равновеликая проекция Ламберта — сохраняет площадь отдельных полигонов, одновременно поддерживая истинное направление от центра[12].
- Поликоническая проекция — нет искажений форм и местности площадей вдоль центрального меридиана [13].
Гномоническая
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Гномоническая | 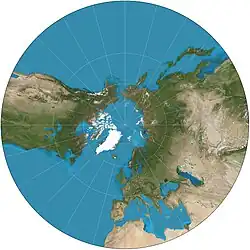 |
Ретроазимутальная
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Ретроазимутальная проекция Крейга | 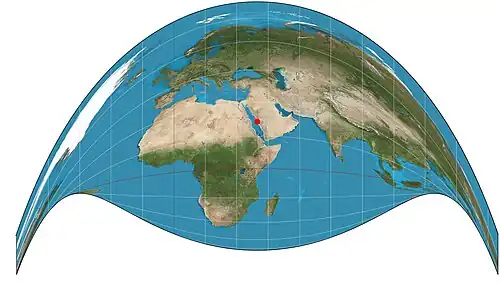 |
Компромиссные проекции
| Проекция | Пример | Создатель | Примечания |
|---|---|---|---|
| Проекция Робинсона | 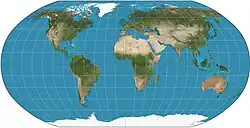 |
Артур Робинсон | Компромисс между конформными и равновеликими проекциями |
| Проекция Ван дер Гринтена | 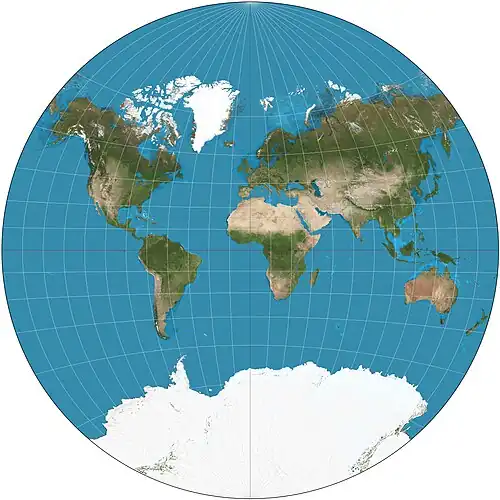 |
Альфонс ван дер Гринтен | Компромисс между конформными и равновеликими проекциями |
| Цилиндрическая проекция Миллера |  |
Osborn Maitland Miller | |
| Тройная проекция Винкеля |  |
Винкель, Освальд | Эта проекция — среднее арифметическое между равнопромежуточной проекцией и проекцией Айтофа |
| Проекция Димаксион |  |
Бакминстер Фуллер | Уменьшает искажения путём потери неразрывности поверхности |
| «Бабочка» Кахилла |  |
Бернард Кахилл | |
| «Бабочка» Уотермана |  |
Стив Уотерман | |
| Проекция Каврайского |  |
В. В. Каврайский | |
| Проекция Вагнера |  |
Эквивалентна проекции Каврайского с коэффициентом горизонтального масштабирования . |
Примечания
- ↑ Картографические проекции. Дата обращения: 19 декабря 2015. Архивировано 14 сентября 2016 года.
- ↑ Carlos A. Furuti. «Polyhedral Maps» Архивная копия от 15 августа 2008 на Wayback Machine.
- ↑ Jarke J. van Wijk Unfolding the Earth: Myriahedral Projections Архивная копия от 20 июня 2020 на Wayback Machine.
- ↑ Carlos A. Furuti. «Interrupted Maps: Myriahedral Maps». Архивная копия от 17 января 2020 на Wayback Machine
- ↑ Geocart Projections. Дата обращения: 19 декабря 2015. Архивировано 26 октября 2015 года.
- ↑ «Polyhedral Maps» by Carlos A. Furuti. Дата обращения: 9 января 2012. Архивировано 15 августа 2008 года.
- ↑ arcgis.com Архивная копия от 4 марта 2016 на Wayback Machine Проекция Кассини — Зольднера
- ↑ Carlos A. Furuti. Conic Projections: Equidistant Conic Projections Архивная копия от 30 ноября 2012 на Wayback Machine
- ↑ Равнопромежуточная коническая проекция. Дата обращения: 26 декабря 2015. Архивировано 27 декабря 2015 года.
- ↑ Проекция равнопромежуточная двух точек
- ↑ arcgis.com Архивная копия от 27 декабря 2015 на Wayback MachineОртографическая проекция
- ↑ Азимутальная равновеликая проекция Ламберта. Дата обращения: 26 декабря 2015. Архивировано 27 декабря 2015 года.
- ↑ arcgis.com Архивная копия от 27 декабря 2015 на Wayback Machine Поликоническая проекция