Теорема Ельмслева о серединах

Теорема Ельмслева о серединах — классическая теорема абсолютной геометрии. Названа в честь Иоганнеса Ельмслева. Часто приводится как иллюстрация к теореме Шаля.

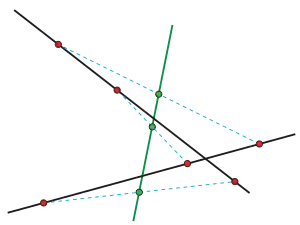
Если точки ${\displaystyle A,B,C,\dots }$ на прямой переводятся движением в точки ${\displaystyle A',B',C',\dots }$, то середины отрезков ${\displaystyle AA',BB',CC',\dots }$ лежат на одной прямой.

Можно считать, что отображение ${\displaystyle m\colon A\mapsto A'}$ меняет ориентацию; если нет то возьмём его композицию с осевой симметрией во второй прямой. Тогда, по теореме Шаля ${\displaystyle m}$ является скользящей симметрией. Отсюда немедленно следует, что все середины лежат на оси скользящей симметрии.

• Martin, George E. (1998), The Foundations of Geometry and the Non-Euclidean Plane, Undergraduate Texts in Mathematics (3rd ed.), Springer-Verlag, p. 384, ISBN 978-0-387-90694-2 {{citation}}: Указан более чем один параметр |ISBN= and |isbn= (справка).