Теорема о трёх перпендикулярах
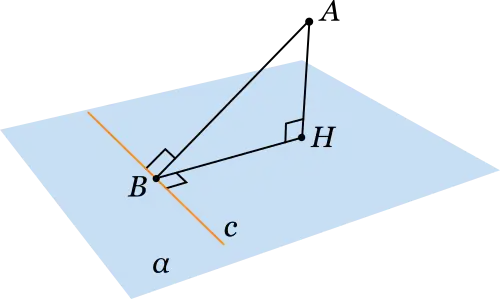
Теоре́ма о трёх перпендикуля́рах — фундаментальная теорема стереометрии[1].
Формулировка
Прямая, проведённая в плоскости через основание наклонной, перпендикулярная к её проекции на эту плоскость, перпендикулярна и самой наклонной.
Более того, верно обратное, то есть если прямая, проведенная на плоскости через основание наклонной, перпендикулярна самой наклонной, то она перпендикулярна и её проекции.
Пример использования
Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.
Решение
Решение: пусть а — прямая и А — точка на ней. Возьмем любую точку Х вне прямой а и проведем через эту точку и прямую а плоскость α. В плоскости α через точку А можно провести прямую b, перпендикулярную а.
Примечания
- ↑ См. например Киселёв, Андрей Петрович (2018). Геометрия по Киселёву. arXiv:1806.06942 [math.HO]., § 302