Фильтр Савицкого — Голея

Фильтр Савицкого — Голея (полиноминальный метод Савицкого — Голея^[1]) это сглаживающий цифровой фильтр, основанный на аппроксимации окрестности каждого измерения степенным полиномом второго и большего порядка^[2][3]. Является линейным симметричным фильтром, а так же методом численного дифференцирования экспериментальных данных.^[4] Фильтр Савицкого — Голея был предложен Савицким и Голеем в 1964 году в виде КИХ-фильтров для разных полиномов и разных размеров скользящего окна, он нашёл широкое применение для сглаживания зашумлённых данных в частности в спектроскопии, где используется для выделения пиков спектров, а также для численного определения^[1] производных^[5]. Метод подвергают модификации для устранения его основных недостатков в конкретных применениях^[6][1].

По существу фильтр Савицкого — Голея является^[2] развитием метода скользящего среднего, и так же является одним из видов свёртки.

Исходная функция обычно представляет собой последовательность данных с фиксированным шагом по оси абсцисс (время, частота и т. п.). Выбирается фиксированный размер скользящего окна в окрестности текущей (центральной) точки. Окно определяет подмножество последовательности исходных данных, которые используются для расчёта сглаживающей фильтрации в текущей точке. На этом подмножестве исходных данных рассчитываются коэффициенты выбранного степенного полинома (обычно 2-й или 3-й степени) с помощью метода наименьших квадратов (МНК). Точка этого полинома, соответствующая абсциссе текущей (центральной) точки, является результатом сглаживания для данной точки. Коэффициенты полинома, рассчитанные для центральной точки, могут быть использованы для расчёта производных с порядком вплоть до степени полинома, что и является методом дифференцирования Савицкого — Голея.^[2]

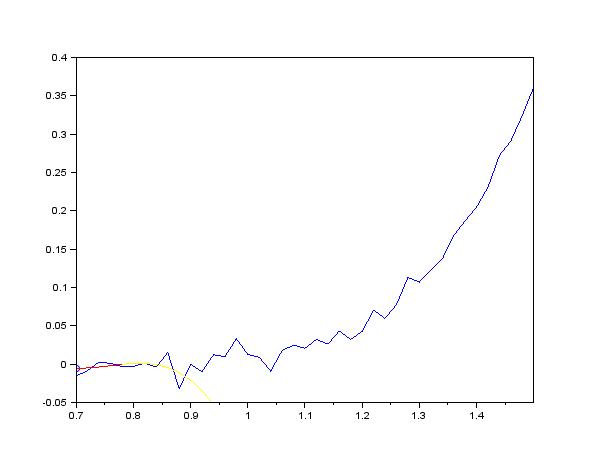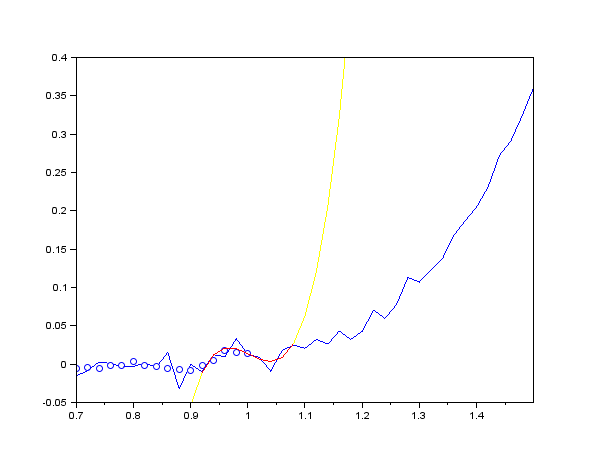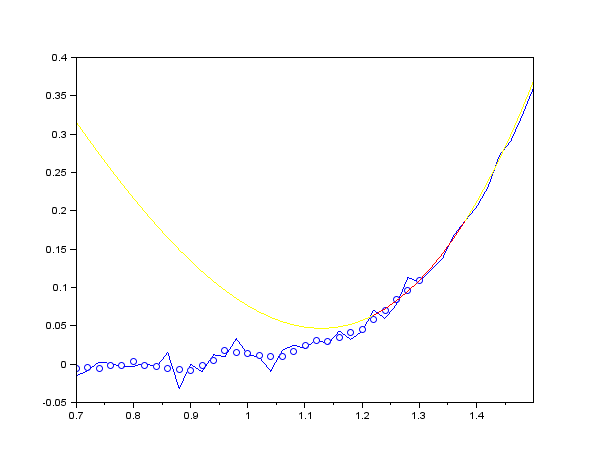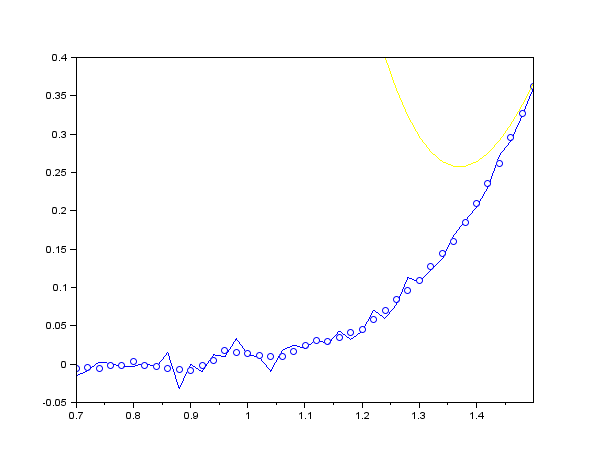
Фильтр Савицкого — Голея обычно реализуют в виде свёртки с постоянными коэффициентами, но это требует фиксированного шага данных по оси абсцисс (время, частота и т. п.), то есть равномерной дискретизации по оси абсцисс^[5]. Коэффициенты свёртки не зависят от исходных данных, а определяются лишь порядком аппроксимирующего степенного полинома и шириной скользящего окна^[5][2]. Коэффициенты свёртки можно взять из таблиц^[5], или рассчитать, например, используя функцию savgol_coeffs библиотеки SciPy. Таким образом, сглаживание исходных данных полностью аналогично работе двустороннего (симметричного) КИХ-фильтра:

${\displaystyle {\begin{aligned}y[n]&=b_{-N}x[n-N]+\cdots +b_{-1}x[n-1]+b_{0}x[n]+b_{1}x[n+1]+\cdots +b_{N}x[n+N]\\&=\sum _{i=-N}^{N}b_{i}\cdot x[n+i],\end{aligned}}}$

где:

• ${\textstyle x[n]}$ — исходная последовательность (например, измерения),
• ${\textstyle y[n]}$ — выходная последовательность (сглаженная функция),
• ${\textstyle N}$ — половина ширины скользящего окна,
• ${\textstyle b_{i}}$ — коэффициенты свёртки, которые зависят только от ширины скользящего окна и от выбранной степени аппроксимирующего полинома.

Аналогично вычисляются производные с порядком вплоть до степени полинома^[2].