Функция голосования
| Функция голосования | |
|---|---|
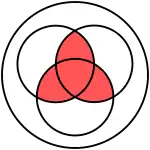 Диаграмма Венна | |
| Определение | |
| Таблица истинности | |
| Нормальные формы | |
| Дизъюнктивная | |
| Конъюнктивная | |
| Полином Жегалкина | |
| Принадлежность предполным классам | |
| Сохраняет 0 | Да |
| Сохраняет 1 | Да |
| Монотонна | Да |
| Линейна | Нет |
| Самодвойственна | Да |
Функция голосования (мажоритарная функция, медиана) — тернарная булева функция, равная тому из двух булевых значений, которое больше раз встретилось среди аргументов.[1][2] То есть функция голосования равна на наборах, в которых 0 или 1 единица (соответственно 3 или 2 нуля) и равна на наборах, в которых2 или 3 единицы (соответственно 1 или 0 нулей). Обозначения: [2], [3], .[4]
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Функция голосования является базисом класса монотонных самодвойственных функций.[3]
Функция голосования является симметричной функцией. Вектор значений симметричной булевой функции:
Функция голосования удовлетворяет условиям и , но не удовлетворяет условиям и .
Отрицание функции голосования
Не менее важной функцией является отрицание функции голосования . Оно равно тому булеву значению, которое встречалось среди аргументов меньшее число раз. Таблица истинности:
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Отрицание функции голосования является базисом класса самодвойственных функций. Она также является симметричной, её вектор значений симметричной функции:
Примечания
- ↑ 3.3. Способы задания булевых функций.
- 1 2 Колпаков, Кочергин, с. 7.
- 1 2 Яблонский, Гаврилов, Кудрявцев, с. 17.
- ↑ Яблонский, Гаврилов, Кудрявцев, с. 51.
Литература
- Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста / под ред. В. В. Донченко. — М.: Наука, 1966. — 120 с. — 10 000 экз.
- Колпаков Р. М., Кочергин В. В. Теория дискретных функций (pdf). Дата обращения: 11 января 2025.