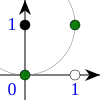
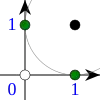
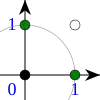
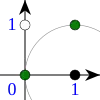
Сферы Хемминга для двоичного двумерного векторного пространства с центрами в различных точках (отмечены чёрным). Сферам принадлежат точки, отмеченные чёрным и зелёным. Точки, отмеченные белым не принадлежат сферам. В каждом из примеров сферам принадлежит ровно три точки (вектора).
Хеммингова сфера  радиуса
радиуса  c центром в точке
c центром в точке  — множество всех векторов (точек) в двоичном векторном пространстве
— множество всех векторов (точек) в двоичном векторном пространстве  находящихся на расстоянии
находящихся на расстоянии  от заданного вектора
от заданного вектора  :
:

Хеммингов шар  радиуса
радиуса  c центром в точке
c центром в точке  — множество всех векторов (точек) в двоичном векторном пространстве
— множество всех векторов (точек) в двоичном векторном пространстве  на расстоянии не более
на расстоянии не более  от заданного вектора
от заданного вектора  :
:

Если размерность двоичного векторного пространства  равна
равна  , то количество точек (векторов), принадлежащих
, то количество точек (векторов), принадлежащих  равно:
равно:

Если размерность двоичного векторного пространства  равна
равна  , то количество точек (векторов), принадлежащих
, то количество точек (векторов), принадлежащих  равно:
равно:

Литература
- Морелос-Сарагоса Р. 1.1.2. Хеммингово расстояние, Хемминговы сферы и корректирующая способность // Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение / пер. с англ. В. Б. Афанасьева. — М.: Техносфера, 2006. — С. 20—23. — (Мир связи). — 2000 экз. — ISBN 5-94836-035-0.