| Распределение хи |
|---|
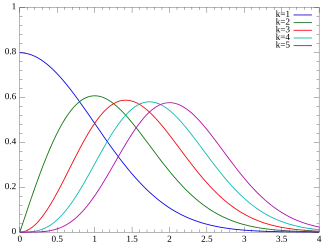 Плотность вероятности Плотность вероятности |
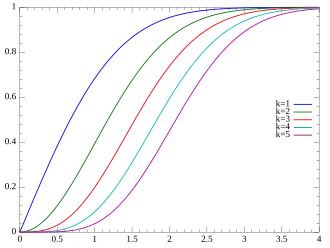 Функция распределения Функция распределения |
| Параметры |
 (степени свободы) (степени свободы) |
| Носитель |
 |
| Плотность вероятности |
 |
| Функция распределения |
 |
| Математическое ожидание |
 |
| Медиана |
примерно  |
| Мода |
 если если  |
| Дисперсия |
 |
| Коэффициент асимметрии |
 |
| Коэффициент эксцесса |
 |
| Дифференциальная энтропия |

 |
| Производящая функция моментов |
См. в тексте |
| Характеристическая функция |
См. в тексте |
Хи-распределение — непрерывное вероятностное распределение случайной величины, являющейся квадратным корнем суммы квадратов независимых нормальных случайных величин. Оно связано с хи-квадрат распределением и является распределением квадратного корня случайной величины, распределённой по закону  .
.
Если  являются независимыми, нормально распределёнными случайными величинами с нулевым математическим ожиданием (средним) и дисперсией равной 1, то статистика
являются независимыми, нормально распределёнными случайными величинами с нулевым математическим ожиданием (средним) и дисперсией равной 1, то статистика

распределена по закону хи. Соответственно, если оценку среднеквадратического отклонения  разделить на
разделить на  , где
, где  — среднее хи-распределения, то получится несмещённая оценка среднеквадратического отклонения нормального распределения. Хи-распределение имеет один параметр —
— среднее хи-распределения, то получится несмещённая оценка среднеквадратического отклонения нормального распределения. Хи-распределение имеет один параметр —  , который задаёт число степеней свободы (то eсть количество
, который задаёт число степеней свободы (то eсть количество  ).
).
Самые известные примеры — распределение Рэлея (число степеней свободы равно двум) и статистика Максвелла — Больцмана (число степеней свободы — три).
Определение
Плотность вероятности
Плотность вероятности хи распределения равна

где  — гамма-функция.
— гамма-функция.
Функция распределения
Функция распределения равна:

где  — регуляризованная гамма-функция.
— регуляризованная гамма-функция.
Производящие функции
Производящая функция моментов равна:

где  — вырожденная гипергеометрическая функция Куммера. Характеристическая функция равна:
— вырожденная гипергеометрическая функция Куммера. Характеристическая функция равна:

Свойства
Моменты
Моменты вычисляются по формуле:

где  — гамма-функция. Первые шесть моментов задаются по следующим формулам:
— гамма-функция. Первые шесть моментов задаются по следующим формулам:






где правые выражения получены, используя рекуррентное соотношение для гамма-функции:

Также из этих выражений можно получить следующие формулы:
Среднее: 
Дисперсия:  — из выражений для первых двух моментов.
— из выражений для первых двух моментов.
Коэффициент асимметрии: 
Коэффициент эксцесса: 
Энтропия
Дифференциальная энтропия задаётся по формуле:

где  — полигамма-функция.
— полигамма-функция.
Связь с другими распределениями
- Если
 , тогда
, тогда  (хи-квадрат-распределение)
(хи-квадрат-распределение)
 (нормальное распределение)
(нормальное распределение)- Если
 , то
, то 
- Если
 , то
, то  (полунормальное распределение) для любых
(полунормальное распределение) для любых 
 (распределение Рэлея)
(распределение Рэлея) (распределение Максвелла)
(распределение Максвелла) (вторая норма от
(вторая норма от  стандартных нормальных случайных величин — хи-распределение с
стандартных нормальных случайных величин — хи-распределение с  степенями свободы)
степенями свободы)- Хи-распределение — специальный случай гамма-распределения, распределение Накагами и нецентрального хи-распределения.
Виды распределений хи и хи-квадрат
| Название | Статистика |
| хи-квадрат распределение |  |
| нецентральное хи-квадрат распределение |  |
| хи-распределение |  |
| нецентральное хи-распределение |  |
Литература
- Martha L. Abell, James P. Braselton, John Arthur Rafter, John A. Rafter, Statistics with Mathematica (1999), 237f.
- Jan W. Gooch, Encyclopedic Dictionary of Polymers vol. 1 (2010), Appendix E, p. 972.
 Плотность вероятности
Плотность вероятности  Функция распределения
Функция распределения