Большой икосододекаэдр

Большой икосододекаэдр
Тип	Однородный звёздчатый многогранник
Комбинаторика
Элементы	32 грани 60 рёбер 30 вершин Χ = 2
Грани	20 треугольников 12 пятиугольников
Конфигурация вершины	3.5/2.3.5/2
Двойственный многогранник	Большой ромбический тридцатигранник
Вершинная фигура
Классификация
Обозначения	U54, C70, W94
Символ Шлефли	r{3,5/2}
Символ Витхоффа	2 | 3 5/2 2 | 3 5/3 2 | 3/2 5/2 2 | 3/2 5/3
Диаграмма Дынкина
Группа симметрии	Ih, [5,3],*532

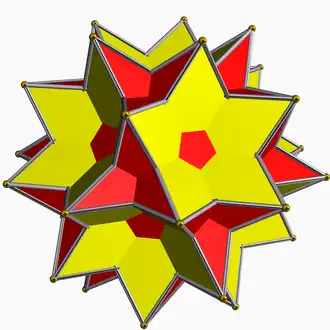
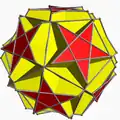
Большой икосододекаэдр — однородный звёздчатый многогранник, имеющий номер однородного многогранника (Uniform polyhedron index) U₅₄. Многогранник имеет 32 грани (20 треугольников и 12 пятиугольников), 60 рёбер и 30 вершин^[1]. Он имеет символ Шлефли r{3,5⁄2}. Многогранник является полным усечением большого звёздчатого додекаэдра и большого икосаэдра. Многогранник независимо обнаружили Хесс в 1878 году^[2], Бэдуру в 1881^[3] и Пич в 1882^[4].

Многогранник назван по аналогии с кубооктаэдром и по аналогии, как из додекаэдра-икосаэдра получили (малый) икосододекаэдр.

Он имеет то же расположение вершин, что и икосододекаэдр, который служит его выпуклой оболочкой. В отличие от большого икосаэдра и большого додекаэдра, большой икосододекаэдр не является звёздчатой формой икосододекаэдра.

Многогранник имеет то же расположение рёбер, что и большой икосогемидодекаэдр (имея общие треугольные грани), и большим додекогемидодекаэдром (имея общие пентаграммные грани).

Большой икосододекаэдр

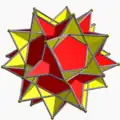Большой додекагемидодекаэдр

Большой икосогемидодекаэдр|-

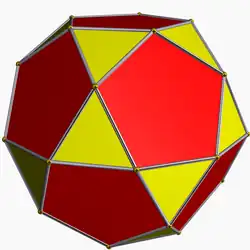Икосододекаэдр (выпуклая оболочка)

Этот многогранник можно считать полным усечением большого икосаэдра:

Усечённый большой звёздчатый додекаэдр является вырожденным многогранником с 20 треугольными гранями из усеченных вершин и 12 (скрытыми) пятиугольными гранями, являющимися усечениями исходных пятиугольных граней, формиурующие большой додекаэдр, вписанный в многогранник и имеющий те же рёбра, что и икосаэдр.

Название	Большой звёздчатый додекаэдр	Усечённый большой звёздчатый додекаэдр	Большой икосододекаэдр	Усечённый большой икосаэдр	Большой икосаэдр
Диаграмма Коксетера
Рисунок

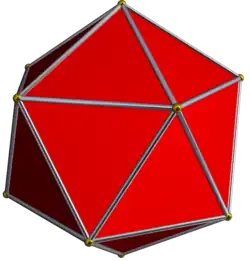Большой ромбический тридцатигранник

Большой ромбический тридцатигранник
Тип	Звёздчатый многогранник
Комбинаторика
Элементы	30 граней 60 рёбер 32 вершины Χ = 2
Грани
Двойственный многогранник	Большой икосододекаэдр
Вершинная фигура -
Классификация
Обозначения	DU54
Символ Шлефли	r{3,5/2}
Группа симметрии	Ih,[5,3],*532

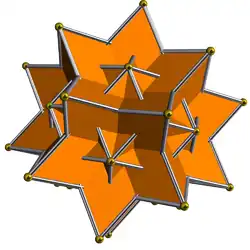
Двойственным многогранником большого икосододекаэдра является большой ромбический тридцатигранник. Это невыпуклое изоэдральное и изотоксальное тело, имеющее 30 пересекающихся ромбических граней. Многогранник можно также назвать большим звёздчатым тридцатигранником.

Большой ромбический тридцатигранник можно построить, увеличивая размер граней ромботриаконтаэдра на множитель ${\displaystyle \tau ^{3}=1+2\tau =2+{\sqrt {5}}}$, где ${\displaystyle \tau }$ является золотым сечением.

• Однородный многогранник
• Ромбический шестидесятиграник

• Weisstein, Eric W. Great icosidodecahedron (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Great rhombic triacontahedron (англ.) на сайте Wolfram MathWorld.
• Uniform polyhedra and duals