Выпуклый слой
Вы́пуклый слой[1] — понятие комплексного анализа, раздела математики, точечное множество
где — выпуклые ограниченные области, причём замыкание [2].
В случае, когда обе области и — концентрические сферы, то получаем частный случай выпуклого слоя — сферический слой[3].
Определение выпуклого слоя
Выпуклый слой — точечное множество комплексно-вещественного пространства
такое, что
- ,
где — выпуклые ограниченные области, причём замыкание [2].
В случае, когда обе области и — концентрические сферы, то получаем частный случай выпуклого слоя — сферический слой[3].
Структура выпуклого слоя
Представим структуру выпуклого слоя в следующем комплексно-вещественном пространстве[2]:
1. Вещественные проекции. Вещественная структура выпуклого слоя выглядит следующим образом. Спроектируем определённые выше точечные множества , на вещественное пространство Получим следующие проекции[2]:
- проекция выпуклой области — выпуклая область ;
- проекция выпуклой области — выпуклая подобласть ;
- проекция области — область .
В этом случае выпуклый слой есть снова разность двух точечных множеств , , а при множество — два непересекающихся интервала оси [2].
2. Комплексные слои. Комплексная структура выпуклого слоя в комплексно-вещественном пространстве выглядит следующим образом. Для этого представим точечные множества в виде множества срезов-«слоёв»[2]:
В этом случае достаточно очевидно, что если , то оба множества и суть двумерные выпуклые области, а если , то множество образуется из множества путём исключения одной точки или некоторой замкнутой кривой со своей внутренностью[4].
Сферический слой

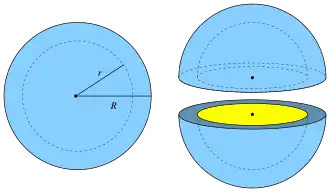
Сферический слой — область, заключённая между двумя концентрическими сферами различных радиусов[5][6][3].
Устаревшие синонимы: сферическая оболочка[7]; шаровой слой[8].
Тонкий сферический слой может называться тонкостенной сферой (англ. thin-walled spherical shell[9])[10].
Сферический слой представляет собой частный случай выпуклого слоя[3].
Определение сферического слоя
Сферический слой — точечное множество комплексного пространства , которое можно определить как следующую разность двух концентрических шаров с центром в точке , где уменьшаемое — открытый шар, а вычитаемое — замкнутый шар[3]:
- ,
или сразу как следующее обобщённое кольцо с центром в начале координат[11][12]:
- .
В случае простейшего комплексно-вещественного пространства сферический слой с центром в начале координат можно определить следующей формулой[11]:
Слой бикруга
Слой бикруга — область, заключённая между двумя концентрическими границами различных бикругов[13].
Слой бикруга — точечное множество комплексного пространства , который можно определить как следующую разность двух концентрических бикругов с центром в начале координат, где вычитаемое — замыкание бикруга[13]:
Примечания
- ↑ Перевод на англ. см. в закладке «Обсуждение» статьи
- 1 2 3 4 5 6 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение, § 3. Выпуклые области, с. 98.
- 1 2 3 4 5 Jaap Korevaar, Jan Wiegerinck. Several Complex Variables, 2011, 1.9 Preview: analytic continuation…, p. 18.
- ↑ Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение, § 3. Выпуклые области, с. 98—99.
- ↑ Weisstein Eric W. Spherical Shell, 2025.
- ↑ Яковлев И. В. Сферический слой, 2025.
- ↑ Сборник задач по общему курсу физики. Электричество и магнетизм, 1977, 17, с. 7; 63, с. 14.
- ↑ Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Мыльные пузыри, с. 91.
- ↑ Aslamazov L. G., Varlamov A. A. The wonders of physics, 2001, 10.1 Soap-bubbles, p. 78.
- ↑ Асламазов Л. Г., Варламов А. А. Удивительная физика, 1987, Мыльные пузыри, с. 62.
- 1 2 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение, с. 91.
- ↑ Яковлев В. И. Классическая электродинамика. Часть 1 электричество и магнетизм, 2003, Пример 1.9, с. 56.
- 1 2 Steven G. Krantz. Function Theory of Several Complex Variables, 2001, 0.3.1 Domains of Holomorphy, p. 8.
Источники
- Асламазов Л. Г., Варламов А. А.. Удивительная физика. Предисл. А. А. Абрикосова. М.: «Наука», 1987. 159 c. (Библиотечка «Квант». Вып. 63.)
- Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
- Сборник задач по общему курсу физики. Электричество и магнетизм. 4-е изд., перераб. и доп. Под ред. И. А. Яковлева. М.: «Наука», 1977. 272 с.: ил.
- Яковлев В. И. Классическая электродинамика. Часть 1 электричество и магнетизм: Учеб. пособие. Новосибирск: Новосиб. Ун-т, 2003. 267 с.: ил.
- Яковлев И. В. Сферический слой // Подготовка к олимпиадам, ДВИ и ЕГЭ по математике и физике Архивная копия от 5 июля 2024 на Wayback Machine
- Aslamazov L. G., Varlamov A. A. The wonders of physics. Scientific Editor A. A. Abrikosov Jr. Translators A. A. Abrikosov Jr & D. Znamenski. Singapore · New Jersey · London · Hong Kong: World Scientific, 2001. [Асламазов Л. Г., Варламов А. А.. Удивительная физика. Предисл. А. А. Абрикосова. М.: «Наука», 1987. 159 c. (Библиотечка «Квант». Вып. 63.)]
- Salomon Bochner, William Ted Martin Several Complex Variables. Princeton: Princeton University Press, 1948. 216 p. [Бохнер С., Мартин У. Т. Функции многих комплексных переменных. Принстон: Издательство Принстонского университета, 1948.]
- Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.
- Steven G. Krantz. Function Theory of Several Complex Variables: Second edition. Providence, Rhode Island: AMS Chelsea Publishing, 1951. 564 p. 1992 held by the American Mathematical Society. Printed with corrections, 2001.
- Weisstein Eric W. Spherical Shell // Wolfram MathWorld Архивная копия от 22 января 2025 на Wayback Machine