Поликруг

Поликру́г^[1] — понятие комплексного анализа, раздела математики, топологическое произведение нескольких плоских кругов, одно из обобщений понятия круга; другое наиболее известное обобщение круга — шар^[2][3].

Синонимы: полидиск^[4]; круговой полицилиндр^[5][3]; шар в поликруговой метрике; шар в ${\displaystyle \rho }$-метрике^[2]; произведение кругов^[6].

Поликруг естественным образом обобщается на полиобласть^[5].

Поликруг есть частный случай полной области Рейнхарта^[7][5].

Поликруг^[1] радиуса ${\displaystyle r}$ с центром в точке ${\displaystyle z_{0}}$ — следующее множество точек ${\displaystyle z}$ комплексного пространства ${\displaystyle C^{n}}$ произвольной размерности ${\displaystyle n}$^[2][8]:

${\displaystyle \Delta ^{n}(z_{0},\,r)=\{z\in \mathbb {C} ^{n}\colon \,\|z-z_{0}\|<r\}=}$

${\displaystyle =\{z=(z_{1},\,z_{2},\,\dots ,\,z_{n})\in \mathbb {C} ^{n}\colon \,{\underset {k}{\max }}|z_{k}-z_{0k}|<r,\,k=1,\,2,\,\dots ,\,n\}=}$.

${\displaystyle =\{z=(z_{1},\,z_{2},\,\dots ,\,z_{n})\in \mathbb {C} ^{n}\colon \,|z_{k}-z_{0k}|<r,\,k=1,\,2,\,\dots ,\,n\}}$.

Синонимы: полидиск^[4]; круговой полицилиндр^[5][3]; шар в поликруговой метрике; шар в ${\displaystyle \rho }$-метрике^[2]; поликруг с равными радиусами^[1]; полицилиндр с равными радиусами^[1][6]; произведение кругов^[1][6].

Так определённый поликруг — это шар с центром ${\displaystyle z_{0}}$ в поликруговой ${\displaystyle \rho }$-метрике. Геометрически поликруг есть топологическое произведение ${\displaystyle n}$ плоских кругов

${\displaystyle \Delta ^{n}(z_{0},\,r)=\Delta (z_{01},\,r)\times \Delta (z_{02},\,r)\times \cdots \times \Delta (z_{0n},\,r),}$

${\displaystyle \Delta (z_{0k},\,r)=\{z_{k}\in \mathbb {C} \colon |z_{k}-z_{0k}|<r\},\,k=1,\,2,\,\dots ,\,n,}$

радиуса ${\displaystyle r}$ с центрами в точках ${\displaystyle z_{0k}}$^[2].

В общем случае поликруг векторного радиуса, или мультирадиуса^[1], ${\displaystyle \mathbf {r} =(r_{1},\,r_{2},\,\dots ,\,r_{n})}$ с центром в точке ${\displaystyle z_{0}}$ — это следующее множество точек^{[2][4][5][3][9]}:

${\displaystyle \Delta ^{n}(z_{0},\,\mathbf {r} )=\{z=(z_{1},\,z_{2},\,\dots ,\,z_{n})\in \mathbb {C} ^{n}\colon |z_{k}-z_{0k}|<r_{k},\,k=1,\,2,\,\dots ,\,n\}}$.

В общем случае поликруг векторного радиуса есть геометрически топологическое произведение ${\displaystyle n}$ плоских кругов с разными радиусами ${\displaystyle r_{k}}$ и одним центром ${\displaystyle z_{0}}$^[5]:

${\displaystyle \Delta ^{n}(z_{0},\,\mathbf {r} )=\Delta (z_{01},\,r_{1})\times \Delta (z_{02},\,r_{2})\times \cdots \times \Delta (z_{0n},\,r_{n}),}$

${\displaystyle \Delta (z_{0k},\,r_{k})=\{z_{k}\in \mathbb {C} \colon |z_{k}-z_{0k}|<r_{k}\},\,k=1,\,2,\,\dots ,\,n,}$

Единичный поликруг — поликруг с центром в начале координат, то есть ${\displaystyle z_{0}=0}$, и единичным радиусом, то есть ${\displaystyle r=1}$^[5].

В общем случае эллиптический полицилиндр с центром в начале координат — это следующее множество точек^[10]:

${\displaystyle E^{n}(\mathbf {r} )=\{z=(z_{1},\,z_{2},\,\dots ,\,z_{n})\in \mathbb {C} ^{n}\colon |z_{k}+{\sqrt {r_{k}^{2}-1}}|<r_{k},\,r_{k}>1,\,k=1,\,2,\,\dots ,\,n\}.}$

В общем случае аналитически скошенный полицилиндр — это множество точек, получающееся из полицилиндра после аффинного преобразования

${\displaystyle z_{k}=b_{k}+\sum \limits _{p=1}^{n}a_{kp}z'_{p},\,k=1,\,2,\,\dots ,\,n}$

комплексного пространства^[11].

Поликруг естественным образом обобщается на полиобласть^[5].

Поликруг есть частный случай полной области Рейнхарта^[7][5].

• Диаграммы поликруга Рейнхарта и Хартогса
• 
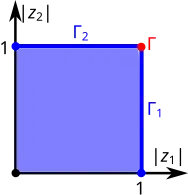  Диаграмма Рейнхарта бикруга в ${\displaystyle \mathbb {C} ^{2}}$
• 
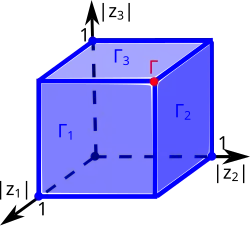  Диаграмма Рейнхарта трикруга в ${\displaystyle \mathbb {C} ^{3}}$
• 
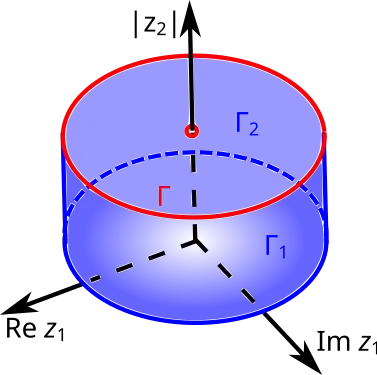  Диаграмма Хартогса бикруга в ${\displaystyle \mathbb {C} ^{2}}$

Граница^[1] поликруга — множество ${\displaystyle \partial \Delta ^{n}}$ всех точек, обладающих следующими двумя свойствами^[2]:

• хотя бы одна координата ${\displaystyle z_{k}}$ принадлежит границе ${\displaystyle k}$-го круга;
• остальные координаты ${\displaystyle z_{l},\,l\neq k,}$ имеют произвольные значения в замкнутых кругах.

Граница ${\displaystyle \partial \Delta ^{n}}$ поликруга ${\displaystyle \Delta ^{n}}$ состоит естественным образом из ${\displaystyle n}$ множеств

${\displaystyle \Gamma _{k}=\{z\in \mathbb {C} ^{n}\colon |z_{k}-z_{0k}|=r_{k},\,|z_{l}-z_{0l}|\leqslant r_{l},\,l\neq k\}}$

размерности ${\displaystyle 2n-1}$, поскольку на ${\displaystyle 2n}$ координат любой точки ${\displaystyle z}$ накладывается одно вещественное условие ${\displaystyle |z_{k}-z_{0k}|=r_{k}}$. Следовательно, и вся граница ${\displaystyle \partial \Delta ^{n}=\bigcup _{k=1}^{n}\Gamma _{k}}$ поликруга ${\displaystyle (2n-1)}$-мерна^[2].

Остов поликруга — ${\displaystyle n}$-мерное пересечение всех множеств границы поликруга ${\displaystyle \Gamma _{k}}$

${\displaystyle \Gamma =\operatorname {Sk} \Delta ^{n}=\partial \Delta _{1}\times \partial \Delta _{2}\times \cdots \times \partial \Delta _{n}=}$

${\displaystyle =\{z\in \mathbb {C} ^{n}\colon |z_{k}-z_{0k}|=r_{k},\,k=1,\,2,\,\dots ,\,n\},}$

которое представляет собой топологическое произведение ${\displaystyle n}$ окружностей^[2][5][4].

Не следует путать с кратно-круговой областью, ${\displaystyle n}$-круговой областью (multicircular domain) и полукруговой областью.

Поликруг естественным образом обобщается на полиобласть^[5].

Полиобласть^[1] ${\displaystyle D=D_{1}\times D_{2}\times \cdots \times D_{n}}$ — топологическое произведение ${\displaystyle n}$ следующих в общем случае плоских многосвязных областей^[5][7][9]:

${\displaystyle D_{k}\subset \mathbb {C} ,\,k=1,\,2,\,\dots ,\,n.}$

Синонимы: поликруговая область^[5][7]; обобщённый полицилиндр^[5][3]; полицилиндрическая область^[7][15].

Если все плоские области ${\displaystyle D_{k}}$ односвязны, то в этом случае полиобласть ${\displaystyle D}$ гомеоморфна шару^[7].

Граница ${\displaystyle \partial D}$ полиобласти ${\displaystyle D}$ состоит естественным образом из ${\displaystyle n}$ множеств

${\displaystyle \Gamma _{k}=\{z\in \mathbb {C} ^{n}\colon \,z_{k}\in \partial D_{k},\,z_{l}\in {\overline {D_{l}}},\,l\neq k\},\quad }$ ${\displaystyle k=1,\,2,\,\dots ,\,n}$

размерности ${\displaystyle 2n-1}$^[5][7].

Остов полиобласти ${\displaystyle D}$ — ${\displaystyle n}$ мерное пересечение всех множеств ${\displaystyle \Gamma _{k}}$

${\displaystyle \Gamma =\partial D_{1}\times \partial D_{2}\times \cdots \times \partial D_{n}=}$

${\displaystyle =\{z\in \mathbb {C} ^{n}\colon \,z_{k}\in \partial D_{k},\,k=1,\,2,\,\dots ,\,n\},}$

которое представляет собой топологическое произведение ${\displaystyle n}$ областей^[5][7].

• Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
• Белошапка В. К. Курс лекций по комплексному анализу. М., 2005. 31 с., ил.
• Соломенцев Е. Д. Поликруг // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская энциклопедия», 1984. 1216 стб., ил. Стб. 405—406.
• Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.
• Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.
• Steven G. Krantz. Function Theory of Several Complex Variables: Second edition. Providence, Rhode Island: AMS Chelsea Publishing, 1951. 564 p. 1992 held by the American Mathematical Society. Printed with corrections, 2001.