Область Хартогса

Диаграмма Хартогса неполной области в $\mathbb {C} ^{2}$

О́бласть Харто́гса (англ. Hartogs domain) — понятие комплексного анализа, раздела математики, обобщение понятия области Рейнхарта. Названа в честь немецкого математика Фридриха Хартогса^[1]^[2]^[3]^[4]^[5].

Синоним: полукруговая область^[1]^[3]^[4].

Область Хартогса естественным образом возникает как область непрерывной сходимости следующего ряда^[4]:

\sum _{k=0}^{\infty }a_{k}(z_{1},\,z_{2},\,\dots ,\,z_{n-1})z_{n}^{k}.

Область Хартогса есть частный случай кругообразной области^[4].

Определение области Хартогса

Область Хартогса (англ. Hartogs domain) — область $D$ комплексного пространства $\mathbb {C} ^{n}$ , $n\geqslant 1$ , имеющая такое свойство, что вместе с каждой точкой $z^{0}=(z_{1}^{0},\,z_{2}^{0},\,\dots ,\,z_{n-1}^{0},\,z_{n}^{0})\equiv ('\!z^{0},\,z_{n}^{0})\in D$ в области $D$ лежат также и все точки следующей окружности^[1]^[2]^[3]^[4]^[5]:

\{('\!z^{0},\,a_{n}+(z_{n}^{0}-a_{n})e^{i\theta _{n}}),\quad 0\leqslant \theta _{n}<2\pi \}.

Так определённая область Хартогса имеет плоскость симметрии $\{z_{n}=a_{n}\}$ ^[1]^[2]^[3].

Область Хартогса имеет следующий автоморфизм^[3]:

w_{n}=a_{n}+(z_{n}-a_{n})e^{i\theta _{n}},\quad '\!w={}'\!z.

Область Хартогса естественным образом возникает как область непрерывной сходимости следующего ряда^[4]:

\sum _{k=0}^{\infty }a_{k}(z_{1},\,z_{2},\,\dots ,\,z_{n-1})z_{n}^{k}.

Полная область Хартогса (англ. complete Hartogs domain) — область Хартогса $D$ , в которой с каждой точкой $z^{0}=(z_{1}^{0},\,z_{2}^{0},\,\dots ,\,z_{n-1}^{0},\,z_{n}^{0})\equiv ('\!z^{0},\,z_{n}^{0})\in D$ в области $D$ лежит следующий круг^[1]^[2]^[6]:

\{('\!z^{0},\,a_{n}+(z_{n}^{0}-a_{n})\lambda _{n}),\quad |\lambda _{n}|\leqslant 1\},

или

\{('\!z^{0},\,z_{n}),\quad |z_{n}-a_{n}|\leqslant |z_{n}^{0}-a_{n}|\}.

Диаграмма Хартогса

Диаграмма Хартогса — образ области Хартогса $D\subset \mathbb {C} ^{n}$ с плоскостью симметрии $\{z_{n}=0\}$ в пространстве размерности $(2n-1)$ , определяемый следующим преобразованием^[1]^[2]:

D\to {}'\!D\times \mathbb {R} _{+}\colon \,('\!z,\,z_{n})\to ('\!z,\,|z_{n}|),

где $\,{}'\!D\subset \mathbb {C} ^{n-1}$ — проекция $D$ в $\mathbb {C} ^{n-1}$ , то есть множество всех $\,'\!z$ для $z\in D$ ^[1]^[2].

Диаграмме Хартогса полной области $D$ вместе с любой точкой $('\!z^{0},\,|z_{n}^{0}|)\in {}'\!D\times \mathbb {R} _{+}\,$ принадлежит и весь следующий отрезок^[2]:

\{('\!z^{0},\,|z_{n}|)\colon \,|z_{n}|\leqslant |z_{n}^{0}|\}.

Диаграмма Хартогса понижает размерность пространства с областью на единицу и в случае $n=2$ вполне наглядна. На рисунке справа показана неполная область Хартогса, причём точка на этой диаграмме Хартогса представляет окружность, тогда как вертикальный отрезок, основание которого находится в области $\,{}'\!D\subset \mathbb {C} ^{n-1}$ , — это круг^[2].

На рисунке внизу на диаграмме Хартогса показаны области из пространства $\mathbb {C} ^{2}$ : шар и бикруг; для бикруга хорошо просматриваются трёхмерные части его границы $\Gamma _{1}$ и $\Gamma _{2}$ , а также его остов $\Gamma$ ^[2].

Диаграммы Хартогса шара и поликруга
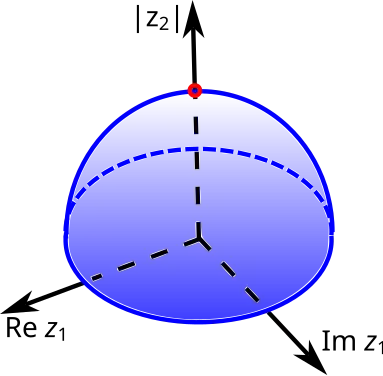$Диаграмма Хартогса шара в C 2 {\displaystyle \mathbb {C} ^{2}}$
Диаграмма Хартогса шара в $\mathbb {C} ^{2}$
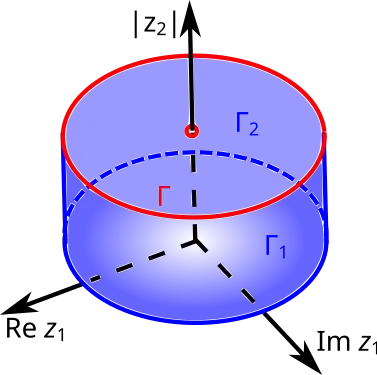$Диаграмма Хартогса бикруга в C 2 {\displaystyle \mathbb {C} ^{2}}$
Диаграмма Хартогса бикруга в $\mathbb {C} ^{2}$

Кругообразная область

Определение кругообразной области

Область Хартогса естественным образом обобщается на кругообразную область^[4].

Орбита, порождаемая точкой $z\in \mathbb {C} ^{n}$ , — точечное множество в комплексном пространстве $\mathbb {C} ^{n}$ вида

\{t^{\alpha _{1}}z_{1},\,t^{\alpha _{2}}z_{2},\,\dots ,\,t^{\alpha _{n}}z_{n}\},\quad

|t|=1,

где $z=(z_{1},\,z_{2},\,\dots ,\,z_{n})\in \mathbb {C} ^{n}$ — любая фиксированная точка; $t\in \mathbb {C}$ — любой комплексный параметр; $\alpha _{1},\,\alpha _{2},\,\dots ,\,\alpha _{n}$ — целые неотрицательные числа, не все равные нулю. Орбита есть топологический образ окружности. Орбита может быть порождена любой из её точек^[4].

Кругообразная область — область $D$ комплексного пространства $\mathbb {C} ^{n}$ , $n\geqslant 1$ , целиком состоящая из некоторых орбит^[4].

В частном случае при $\alpha _{1}=\alpha _{2}=\cdots =\alpha _{n}=1$ получается круговая область, а при $\alpha _{1}=\alpha _{2}=\cdots =\alpha _{n-1}=0$ , $\alpha _{n}=1$ — область Хартогса^[4].

В более общем случае кругообразная область называется кругообразным точечным множеством^[4].

Обобщение кругообразной области — кругообразная область с произвольными целыми показателями $\alpha _{1},\,\alpha _{2},\,\dots ,\,\alpha _{n}$ была впервые изучена французским математиком А. Картаном^[7].

Завершение кругообразной области

Завершение кругообразной области — полученная из исходной кругообразной области $D$ минимальная полная кругообразная область ${\tilde {D}}$ , другими словами, это множество дисков

(t^{\alpha _{1}}z_{1},\,t^{\alpha _{2}}z_{2},\,\dots ,\,t^{\alpha _{n}}z_{n}),\quad

0<|t|\leqslant 1,

которые соответствуют орбитам, которые составляют исходную кругообразную области $D$ ^[7].

Синоним: геометрическое завершение кругообразной области^[8].

В произвольной области комплексной плоскости $\mathbb {C}$ всегда существует некоторая аналитическая функция. Но, с другой стороны, пространство переменных

z,\,u_{1},\,u_{2},\,\dots ,\,u_{n}\in \mathbb {C} \times \underbrace {\mathbb {R} \times \mathbb {R} \times \cdots \times \mathbb {R} } _{\text{n раз}},\quad n\geqslant 1

содержит такие пары областей $D$ , ${\tilde {D}}$ , $D\subset {\tilde {D}}$ , что любая функция, аналитическая в $D$ , остаётся аналитической и в ${\tilde {D}}$ . Этот факт, который имеет место при аналитическом продолжении, относится только к природе комплексной области $D$ , а не к любой аналитической функции, которая определенна в $D$ . Этот факт называется аналитическим расширением (англ. analytic completion), а область ${\tilde {D}}$ называется аналитическим расширением области $D$ ^[9].

Теорема. Завершение ${\tilde {D}}$ кругообразной области $D$ есть тоже область пространства. Область ${\tilde {D}}$ есть аналитическое расширение области $D$ в том случае, когда начало координат $z_{1}=z_{2}=\cdots =z_{n}=0$ принадлежит области $D$ ^[7].

Кратно-кругообразная область

Область Рейнхарта естественным образом обобщается на кратно-кругообразную область, частный случай кругообразной области^[10].

Введём следующие $m$ параметров $t_{1},\,t_{2},\,\dots ,\,t_{m}$ и организуем их в следующие $n$ одночленов

\beta _{j}(t)=t_{1}^{\alpha _{j1}}t_{2}^{\alpha _{j2}}\dots t_{m}^{\alpha _{jm}},\quad j=1,\,2,\,\dots ,\,n,

где показатели степени $\alpha _{j1},\,\alpha _{j2},\,\dots ,\,\alpha _{jm}$ — неотрицательные целые числа^[11].

Пусть определение орбиты следующее:

\{\beta _{1}(t)z_{1},\,\beta _{2}(t)z_{2},\,\dots ,\,\beta _{n}(t)z_{n}\},\quad

|t_{1}|=|t_{2}|=\cdots =|t_{m}|=1,

а определение диска соответственно такое^[11]:

(\beta _{1}(t)z_{1},\,\beta _{2}(t)z_{2},\,\dots ,\,\beta _{1}(n)z_{n}),\quad

0<|t_{1}|,\,|t_{2}|,\,\dots ,\,|t_{m}|\leqslant 1.

Кратно-кругообразная область — область $D$ комплексного пространства $\mathbb {C} ^{n}$ , $n\geqslant 1$ , целиком состоящая из некоторых этих орбит^[11].

Теорема для кругообразной области остаётся истинной и для кратно-кругообразной области:

Теорема. Завершение ${\tilde {D}}$ кратно-кругообразной области $D$ есть тоже область пространства. Область ${\tilde {D}}$ есть аналитическое расширение области $D$ в том случае, когда начало координат $z_{1}=z_{2}=\cdots =z_{n}=0$ принадлежит области $D$ ^[11].

При $m=n$ и $\beta _{j}(t)=t_{j}$ получается наиболее важный вид кратно-кругообразной области, а именно область Рейнхарта. В том случае, когда начало координат принадлежит области Рейнхарта $D$ , её аналитическое расширение — выпуклая область Рейнхарта ${\tilde {D}}$ . Так полученная область ${\tilde {D}}$ называется рейнхартовым аналитическим расширением области^[10].

Примечания

1 2 3 4 5 6 7 Чирка Е. М. Гартогса область, 1977.
1 2 3 4 5 6 7 8 9 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 18.
1 2 3 4 5 Владимиров В. С. Методы теории функций многих комплексных переменных, 1964, § 7. Голоморфные отображения, б. Группа автоморфизмов, с. 63.
1 2 3 4 5 6 7 8 9 10 11 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 7. Кругообразные области, с. 110.
1 2 Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 9.5 Exercises, p. 185.
↑ Владимиров В. С. Методы теории функций многих комплексных переменных, 1964, § 7. Голоморфные отображения, б. Группа автоморфизмов, с. 64.
1 2 3 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 7. Кругообразные области, с. 111.
↑ Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 1. Предварительные сведения, с. 93.
↑ Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение, с. 90.
1 2 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 8. Кратно-кругообразные области, с. 114.
1 2 3 4 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 8. Кратно-кругообразные области, с. 113.

Источники

Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
Владимиров В. С. Методы теории функций многих комплексных переменных / Предисловие академика Н. Н. Боголюбова. М.: «Наука», 1964. 411 с.: ил.
Чирка Е. М. Гартогса область // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская Энциклопедия», 1977. 1152 стб., ил. Стб. 893.
Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.
Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.

[_75e876d443857e1c-1] 1 2 3 4 5 6 7 Чирка Е. М. Гартогса область, 1977.

[_c72275ef460c960a-2] 1 2 3 4 5 6 7 8 9 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 18.

[_fae3eef6cc3b28db-3] 1 2 3 4 5 Владимиров В. С. Методы теории функций многих комплексных переменных, 1964, § 7. Голоморфные отображения, б. Группа автоморфизмов, с. 63.

[_846af01a545993d1-4] 1 2 3 4 5 6 7 8 9 10 11 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 7. Кругообразные области, с. 110.

[_df3ce4260d29e851-5] 1 2 Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 9.5 Exercises, p. 185.

[_bd6711f6a928b4f6-6] Владимиров В. С. Методы теории функций многих комплексных переменных, 1964, § 7. Голоморфные отображения, б. Группа автоморфизмов, с. 64.

[_800f8d1a531ac7ea-7] 1 2 3 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 7. Кругообразные области, с. 111.

[_bb75923f226e9406-8] Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 1. Предварительные сведения, с. 93.

[_d12ccf307263e4d6-9] Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение, с. 90.

[_d76689b23758c2e8-10] 1 2 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 8. Кратно-кругообразные области, с. 114.

[_f0887ab2455641a9-11] 1 2 3 4 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 8. Кратно-кругообразные области, с. 113.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]