Многогранник Ханнера

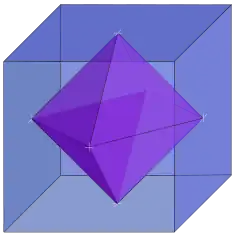
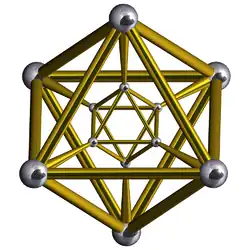
Многогранники Ханнера — класс выпуклых многогранников, которые можно получить рекурсивно из отрезка при помощи двух операций: взятие прямого произведения и переход к двойственному многограннику.

Названы в честь Олофа Ханнера, который рассмотрел их в 1956 году.^[1]

Многогранники Ханнера образуют минимальный класс многогранников, удовлетворяющий следующим условиям:^[2]

• Отрезок прямой является одномерным многогранником Ханнера.
• Прямое произведение двух многогранников Ханнера является многогранником Ханнера. (Его размерность равна сумме размерностей двух исходных многогранников.)
• Многогранник двойственный к многограннику Ханнера является многогранником Ханнера. (Этот многогранник имеет ту же размерность, что и исходный.)

• Квадрат — это многогранник Ханнера как прямое произведение двух отрезков.
• Куб — это многогранник Ханнера как прямое произведение трех отрезков.
• Октаэдр — также многогранник Ханнера как многогранник, двойственный к кубу.

В размерности три любой многогранник Ханнера комбинаторно эквивалентен одному из этих двух видов многогранников.^[5] В высших измерениях аналоги куба и октаэдра, гиперкубы и гипероктаэдры, также являются многогранниками Ханнера. Однако есть и другие примеры. В частности восьмигранная призма — четырёхмерная призма с основанием октаэдр. Она является многогранником Ханнера, как произведение октаэдра на отрезок.

• Многогранники Ханнера центрально-симметричны.

• Любой многогранник Ханнера комбинаторно эквивалентен многограннику с координатами любой вершины, принимающей значения 0, 1 или −1.^[6]

• Общее число граней ${\displaystyle d}$-мерного многогранника Ханнера равно ${\displaystyle 3^{d}}$.
  • ${\displaystyle 3^{d}}$-гипотеза Калая состоит в том, что это число минимально для центрально-симметричных многогранников.^[3]

• Противоположные грани многогранника Ханнера не пересекаются, и вместе содержат все вершины многогранника.
  • В частности, выпуклая оболочка двух таких граней есть весь многогранник.^[6][7]
    • Как следствие из этого факта, все грани многогранника Ханнера имеют одинаковое число вершин.
      • Однако грани могут не быть изоморфны друг другу. Например, в восьмигранной призмы две грани октаэдра, а остальные восемь граней — треугольных призм.
  • Двойственное свойство состоит в том, что противоположные вершины смежны со всеми гранями многогранника.

• Объём Малера, то есть произведение объёмов самого многогранника и его двойственного, для многогранника Ханнера то же, что у куба.
  • Гипотеза Малера состоит в том, что среди центрально-симметричных выпуклых тел этот объём достигает минимума на многогранниках Ханнера.^[8]

• Число комбинаторных типов многогранников Ханнера размерности d такое же, как число последовательно-параллельных графов с d рёбрами.^[4] Для d = 1, 2, 3, …, это последовательность A058387 в OEIS.

  1, 1, 2, 4, 8, 18, 40, 94, 224, 548, …