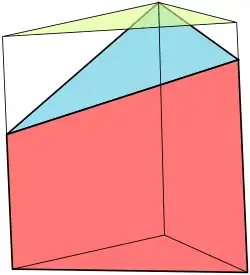
Треугольная призма
Треугольная призма — призма с тремя боковыми гранями. Этот многогранник имеет в качестве граней треугольное основание, его копию, полученную в результате параллельного переноса и 3 грани, соединяющие соответствующие стороны. Прямая треугольная призма имеет прямоугольные боковые стороны, в противном случае призма называется косой.
Однородная треугольная призма — это прямая треугольная призма с равносторонним основанием и квадратными боковыми сторонами.
Призма является пятигранником, у которого две грани параллельны, в то время как нормали трёх других лежат в одной плоскости (которая не обязательно параллельна основаниям). Эти три грани являются параллелограммами. Все сечения, параллельные основаниям, являются одинаковыми треугольниками.
Полуправильный (однородный) многогранник
Прямая треугольная призма является полуправильным многогранником или, более обще, однородным многогранником, если основание является правильным треугольником, а боковые стороны — квадратами.
Этот многогранник можно рассматривать как усечённый треугольный осоэдр, представленный символом Шлефли t{2,3}. Его также можно рассматривать как прямое произведение треугольника на отрезок, что представляется как {3}x{}. Двойственным многогранником треугольной призмы является треугольная бипирамида.
Группой симметрии прямой призмы с треугольным основанием является D3h порядка 12. Группой вращения служит D3 с порядком 6. Группа симметрии не содержит центральную симметрию.
Объём
Объём любой призмы равен произведению площади основания на расстояние между основаниями. В нашем случае, когда основание треугольно, нужно просто вычислить площадь треугольника и умножить на длину призмы:
где b — длина стороны основания, h равна высоте треугольника, а l равна расстоянию между треугольниками.
Усечённая треугольная призма
Усечённая прямая треугольная призма имеет одну усечённую треугольную грань[1].
Гранение
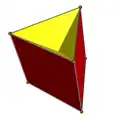
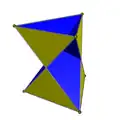
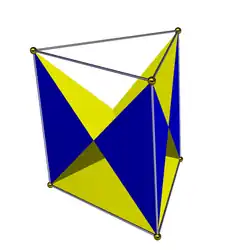
Имеется полная D2h симметрия гранений (удаление части многогранника, не создавая новые вершины, пересечение рёбер новоё вершиной не считается) треугольной призмы. Получающиеся многогранники имеются многогранники с 6 гранями в виде равнобедренного треугольника, один многогранник сохраняет исходные верхний и нижний треугольники, и один сохраняет исходные квадраты. Две симметрии гранения C3v имеют один базовый треугольник, 3 грани в виде боковых самопересекающихся квадратов и 3 грани в виде равнобедренных треугольников.
| Выпуклые | Гранение | |||
|---|---|---|---|---|
| Симметрия D3h | Симметрия C3v | |||
 |
 |
 |
 |
 |
| 2 {3} 3 {4} |
3 {4} 6 () v { } |
2 {3} 6 () v { } |
1 {3} 3 t'{2} 6 () v { } |
1 {3} 3 t'{2} 3 () v { } |
Связанные многогранники и мозаики
| Многоугольник | 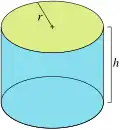 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
| n | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|
| Название | {2} || t{2} | {3} || t{3} | {4} || t{4} | {5} || t{5} | {6} || t{6} |
| Купол | 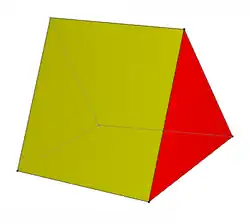 Диагональный купол |
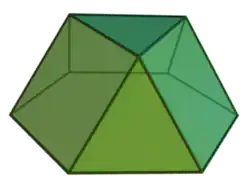 Трёхскатный купол |
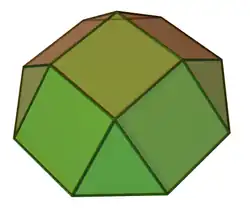 Четырёхскатный купол |
 Пятискатный купол |
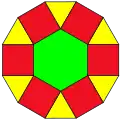 Шестискатный купол (плоский) |
| Связанные однородные многогранники |
Треугольная призма |
Кубооктаэдр |
Ромбокубо- октаэдр |
Ромбоикосо- додекаэдр |
Ромботри- шестиугольная мозаика |
Варианты симметрии
Этот многогранник топологически является частью последовательности однородных усечённых многогранников с вершинными конфигурациями (3.2n.2n) и имеющими симметрию [n,3] группы Коксетера.
| Варианты симметрии *n32 усечённых мозаик: 3.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Симметрия *n32 [n,3] |
Сферическая | Евклидова | Компактная гиперболич. | Параком- пактная |
Некомпактная гиперболич. | ||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] |
[12i,3] | [9i,3] | [6i,3] | |
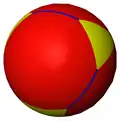
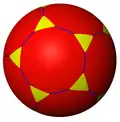
| Усечённые фигуры |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Конфигурация | 3.4.4 | 3.6.6 | 3.8.8 | 3.10.10 | 3.12.12 | 3.14.14 | 3.16.16 | 3.∞.∞ | 3.24i.24i | 3.18i.18i | 3.12i.12i |
| Разделённые фигуры |
 |
 |
 |
 |
 |
 |
 |
||||
| Конфигурация | V3.4.4 | V3.6.6 | V3.8.8 | V3.10.10 | V3.12.12 | V3.14.14 | V3.16.16 | V3.∞.∞ | |||
Этот многогранник топологически является частью последовательности рёберно усечённых многогранников с вершинной фигурой (3.4.n.4), которая продолжается как умощения гиперболической плоскости. Эти вершинно-транзитивные фигуры имеют зеркальную симметрию (*n32).
| Варианты симметрии *n42 расширенных мозаик: 3.4.n.4 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Симметрия *n32 [n,3] |
Сферическая | Евклидова | Компактная гиперболическая |
Паракомпактная | ||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Фигура |  |
 |
 |
 |
 |
 |
 |
 |
| Конфигурация | 3.4.2.4 | 3.4.3.4 | 3.4.4.4 | 3.4.5.4 | 3.4.6.4 | 3.4.7.4 | 3.4.8.4 | 3.4.∞.4 |
Составные тела
Имеется 4 однородных составных тела из треугольных призм:
- соединение четырёх треугольных призм;
- соединение восьми треугольных призм;
- соединение десяти треугольных призм;
- соединение двадцати треугольных призм.
Соты
Существует 9 однородных сот, которые включают треугольные призмы:
- гироудлинённые альтернированные кубические соты
- удлинённые альтернированные кубические соты
- плосконосые квадратно-призматические соты
- треугольные призматические соты
- тришестиугольные призматические соты
- усечённые шестиугольные призматические соты
- ромботришестиугольные призматические соты
- плосконосые шестиугольные призматические соты
- удлинённые треугольные призматические соты
Связанные многогранники
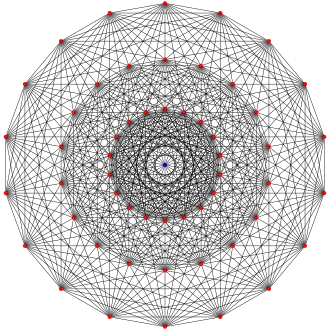
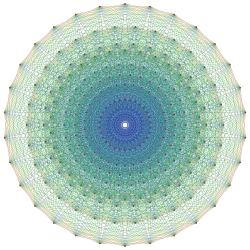
Треугольная призма является первой в пространственной серии полуправильных многогранников. Каждый последующий однородный многогранник имеет в качестве вершинной фигуры предыдущий многогранник. Торольд Госсет обнаружил эту серию в 1900 году как содержащую все виды граней правильных многомерных многогранников, содержащую все симплексы и ортоплексы (правильные треугольники и квадраты в случае треугольной призмы). В нотации Коксетера треугольной призме соответствует символ −121.
| k21 в пространстве размерности n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Пространство | Конечное | Евклидово | Гиперболическое | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Группа Коксетера |
E₃=A₂A₁ | E₄=A₄ | E₅=D₅ | E₆ | E₇ | E₈ | E₉ = Ẽ₈ = E₈+ | E₁₀ = T₈ = E₈++ | |||
| Диаграмма Коксетера |
|||||||||||
| Симметрия | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Порядок | 12 | 120 | 192 | 51 840 | 2 903 040 | 696 729 600 | ∞ | ||||
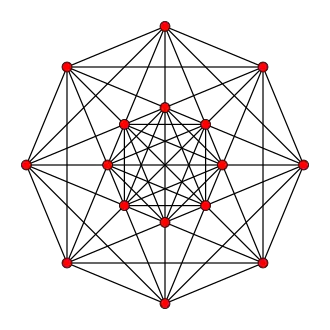
| Граф |  |
 |
 |
 |
 |
 |
- | - | |||
| Обозначение | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
Четырёхмерное пространство
Треугольная призма существует как ячейка в большом числе четырёхмерных однородных четырёхмерных многогранников, включая:
| тетраэдральная призма |
октаэдральная призма |
кубооктаэдрическая призма |
икосаэдральная призма |
икосододекаэдральная призма |
усечённая додекаэдральная призма | ||
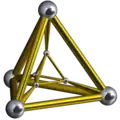 |
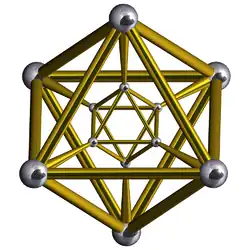 |
 |
 |
 |
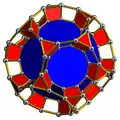 | ||
| Ромбоикосидодекаэдральная призма |
Ромбокубоктаэдральная призма |
Усечённая кубическая призма |
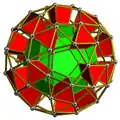
Плосконосая додекаэдральная призма |
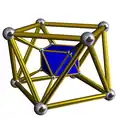
n-угольная антипризматическая призма | |||
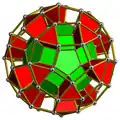 |
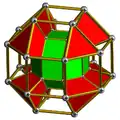 |
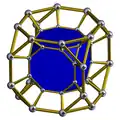 |
 |
 | |||
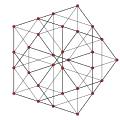
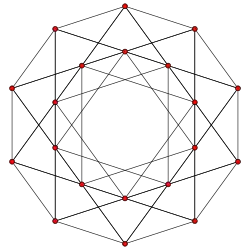
| Рёберноусечённая 5-ячейка |
Кантиусечённая 5-ячейка |
Рансинированная 5-ячейка |
Рансиусечённая 5-ячейка |
Cantellated tesseract |
Кантиусечённый тессеракт |
Рансинированный тессеракт |
Рансиусечённый тессеракт |
 |
 |
 |
 |
 |
 |
 |
 |
| Кантелированная 24-ячейка |
Кантиусечённая 24-ячейка |
Рансинированная 24-ячейка |
Рансиусечённая 24-ячейка |
Кантелированная 120-ячейка |
Кантиусечённая 120-ячейка |
Рансинированная 120-ячейка |
Рансиусечённая 120-ячейка |
 |
 |
 |
 |
 |
 |
 |
 |
См. также
Примечания
- ↑ William F. Kern, James R Bland,Solid Mensuration with proofs, 1938, p.81
Ссылки
- Weisstein, Eric W. Triangular prism (англ.) на сайте Wolfram MathWorld.
- Interactive Polyhedron: Triangular Prism
- surface area and volume of a triangular prism