Треугольные призматические соты
| Треугольные призматические соты | |
|---|---|
 | |
| Тип | Однородные соты |
| Символ Шлефли | {3,6}×{∞} or t0,3{3,6,2,∞} |
| Диаграммы Коксетера | |
| Симметрия | [6,3,2,∞] [3[3],2,∞] [(3[3])+,2,∞] |
| Двойственные | Шестиугольные призматические соты |
| Свойства | вершинно транзитивны |
Треугольные призматические соты — замощение трёхмерного пространства. Соты состоят полностью из треугольных призм.
Соты строятся из треугольной мозаики, вытянутой в призмы.
Соты входят в список 28 выпуклых однородных сот.
Связанные соты
Шестиугольные призматические соты
| Шестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | {6,3}×{∞} or t0,1,3{6,3,2,∞} |
| Диаграмма Коксетера |
|
| Типы ячеек | 4.4.6 |
| Вершинная фигура | Треугольная бипирамида |
| Симметрия | [6,3,2,∞] [3[3],2,∞] |
| Двойственные | Треугольные призматические соты |
| Свойства | вершинно транзитивны |
Шестиугольные призматические соты являются замощением трёхмерного пространства шестиугольными призмами.
Соты строятся из шестиугольной мозаики, вытянутой в призмы.

Соты входят в список 28 выпуклых однородных сот.
Эти соты могут быть альтернированы в повёрнутые тетраэдрально-октаэдральные соты с парами тетраэдров в промежутках между октаэдрами (вместо треугольных бипирамид).
Тришестиугольные призматические соты
| Тришестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | r{6,3}x{∞} or t1,3{6,3}x{∞} |
| Вершинная фигура | Прямоугольная бипирамида |
| Диаграмма Коксетера | |
| Симметрия | [6,3,2,∞] |
| Двойственные | Ромбические призматические соты |
| Свойства | вершинно транзитивны]] |
Тришестиугольные призматические соты являются замощением трёхмерного пространства шестиугольными призмами и треугольными призмами в отношении 1:2.
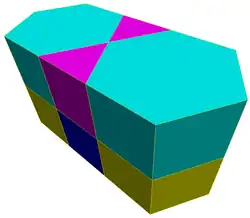
Соты строятся из тришестиугольной мозаики, вытянутой в призмы.
Соты входят в список 28 выпуклых однородных сот.
Усечённые шестиугольные призматические соты
| Усечённые шестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | t{6,3}×{∞} or t0,1,3{6,3,2,∞} |
| Диаграмма Коксетера | |
| Типы ячеек | 4.4.12 3.4.4 |
| Тип граней | {3}, {4}, {12} |
| Рёберные фигцры | Квадрат, Равнобедренный треугольник |
| Вершинная фигура | Треугольная бипирамида |
| Симметрия | [6,3,2,∞] |
| Двойственные | Трижды треугольные призматические соты |
| Свойства | вершинно транзитивны |
Усечённые шестиугольные призматические соты являются замощением трёхмерного пространства. Соты состоят их двенадцатиугольных призм и треугольных призм в отношении 1:2.
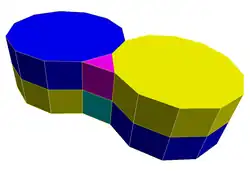
Соты строятся из усечённых шестиугольных мозаик, вытянутых в призмы.
Соты входят в список 28 выпуклых однородных сот.
Ромботришестиугольные призматические соты
| Ромботришестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Вершинная фигура | Трапецеидальня бипирамида |
| Символ Шлефли | rr{6,3}×{∞} or t0,2,3{6,3,2,∞} s2{3,6}×{∞} |
| Диаграмма Коксетера | |
| Симметрия | [6,3,2,∞] |
| Двойственные | Дельтовидные тришестиугольные призматические соты |
| Свойства | вершинно транзитивны |
Ромботришестиугольные призматические соты являются замощением трёхмерного пространства. Соты состоят из шестиугольных призм, кубов и треугольных призм в отношении 1:3:2.
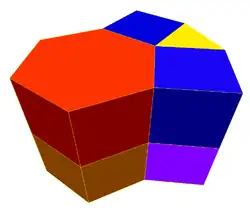
Соты строятся из ромботришестиугольной мощаики, вытянутой в призмы.
Соты входят в список 28 выпуклых однородных сот.
Плосконосые шестиугольные призматические соты
| Плосконосые шестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | sr{6,3}×{∞} |
| Диаграмма Коксетера | |
| Симметрия | [(6,3)+,2,∞] |
| Двойственные | Цветочные пятиугольные призматические соты |
| Свойства | вершинно транзитивны |
Плосконосые шестиугольные призматические соты являются замощением трёхмерного пространства. Соты состоят из шестиугольных призм и треугольных призм в отношении 1:8.
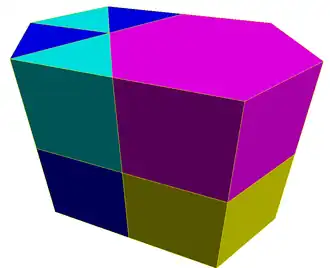
Соты строятся из плосконосых шестиугольных мозаик, вытянутых в призмы.
Соты входят в список 28 выпуклых однородных сот.
Усечённые тришестиугольные призматические соты
| Усечённые тришестиугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | tr{6,3}×{∞} или t0,1,2,3{6,3,2,∞} |
| Диаграмма Коксетера | |
| Симметрия | [6,3,2,∞] |
| Вершинная фигура | неправильная. треугольная Бипирамида |
| Двойственные | Разделённые ромбические (кисромбические) призматические соты |
| Свойства | вершинно транзитивны |
Усечённые тришестиугольные призматические соты являются замощением трёхмерного пространства. Соты состоят из двенадцатиугольных пирамид, шестиугольных призм, и кубов в отношении 1:2:3.
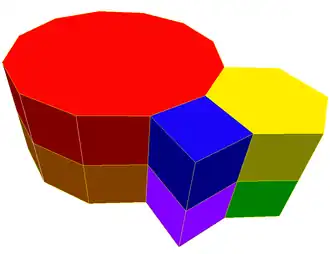
Соты строятся из усечённых тришестиугольных мозаик, вытянутых в призмы.
Соты входят в список 28 выпуклых однородных сот.
Удлинённые треугольные призматические соты
| Удлинённые треугольные призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | {3,6}:e×{∞} s{∞}h1{∞}×{∞} |
| Диаграмма Коксетера | |
| Симметрия | [∞,2+,∞,2,∞] [(∞,2)+,∞,2,∞] |
| Двойственные | Призматические пятиугольные призматические соты |
| Свойства | вершинно транзитивны |
Удлинённые треугольные призматические соты являются замощением (сотами) трёхмерного пространства. Соты состоят из кубов и треугольных призм в отношении 1:2.

Соты строятся из удлинённой треугольной мозаики, вытянутой в призмы.
Соты входят в список 28 выпуклых однородных сот.
Повёрнутые треугольные призматические соты
| Повёрнутые треугольные призматические соты | |
|---|---|
| Тип | Выпуклые однородные соты |
| Символ Шлефли | {3,6}:g×{∞} {4,4}f{∞} |
| Типы ячеек | (3.4.4) |
| Типы граней | {3}, {4} |
| Вершинная фигура | 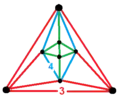 |
| Кристаллографическая группа | ? |
| Двойственные | ? |
| Свойства | вершинно транзитивны |
Повёрнутые треугольные призматические соты являются замощением трёхмерного пространства треугольными призмами. Соты вершинно однородны с 12 треугольными призмами на одну вершину.


Соты можно рассматривать как параллельные слои квадратной мозаики с чередующимся сдвигом, вызванным слоями сдвоенных пар треугольных призм. Призмы в каждом слое повёрнуты на 90º по отношению к следующему уровню.
Соты входят в список 28 выпуклых однородных сот.
Пары треугольных призм можно скомбинировать, чтобы создать ячейки в виде двускатных повёрнутых бикуполов. Получающиеся соты тесно связаны, но не эквивалентны — они имеют то же самое число вершин и рёбер, но различаются двумерными гранями и трёхмерными ячейками.
Скрученно удлинённые призматические соты
| Скрученно удлинённые призматические соты | |
|---|---|
| Тип | Однородные соты |
| Символ Шлефли | {3,6}:ge×{∞} {4,4}f1{∞} |
| Вершинная фигура | 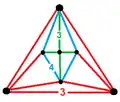 |
| Группа симметрии | ? |
| Двойственные | - |
| Свойства | вершинно транзитивны |
Скрученно удлинённые призматические соты являются замощением трёхмерного пространства. Они состоят из кубов и треугольных призм в отношении 1:2.


Соты созданы чередующимися слоями кубов и треугольных призм с призмами, повёрнутыми на 90º.
Соты связаны с удлинёнными треугольными призматическими сотами, в которых треугольные призмы имеют одну и ту же ориентацию.
См. также
Примечания
- George Olshevsky. Uniform Panoploid Tetracombs. — Manuscript, 2006. (Полный список 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетриасот)'
- Branko Grünbaum. Uniform tilings of 3-space.. — Geombinatorics. — 1994. — С. 49 – 56.
- Norman Johnson. Uniform Polytopes. — Manuscript. — 1991.
- H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H.S.M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss,. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini. Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative. — Mem. Società Italiana della Scienze. — 1905. — С. 75–129. — (Ser.3). (Развёртки правильных и полуправильных многогранников)
- Richard Klitzing, 3D Euclidean Honeycombs, tiph
- Однородные соты в 3-мерном пространстве VRML модели