Задача об иголке

Задача об иголке состоит в определении минимальной площади фигуры на плоскости, в которой единичный отрезок, «иглу», можно развернуть на 180 градусов, вернув его в исходное положение с обращённой ориентацией. Такое возможно проделать в круге радиуса 1/2. Другой пример — фигура, ограниченная дельтоидой, — показан на картинке, он имеет меньшую площадь.

Оказывается, что можно построить фигуру с произвольно малой площадью.

Этот вопрос рассматривал Какея. Он доказал, что для выпуклых областей минимальная площадь достигается для равностороннего треугольника с высотой 1. Его площадь равна ${\displaystyle 1/{\sqrt {3}}}$^[1].

Возможно, Какея также выдвинул гипотезу, что фигура, ограниченная дельтоидой, как на рисунке, имеет наименьшую площадь. Это утверждение было опровергнуто Безиковичем.

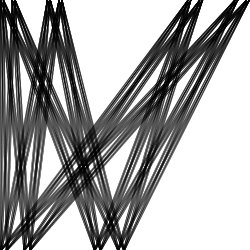
А. С. Безикович построил компактное множество ${\displaystyle K}$ нулевой меры, содержащее единичный отрезок в любом направлении; такие множества называются множествами Безиковича.

Отсюда легко следует, что иглу можно развернуть в фигуре произвольно малой площади. Действительно, легко видеть, что единичный круг можно разбить на секторы и одними параллельными переносами поместить в произвольно малую окрестность множества ${\displaystyle K}$.

Заметим, что единичный отрезок можно передвинуть на параллельную прямую в фигуре произвольно малой площади. Поэтому, повернув отрезок в одном секторе, его можно перетащить в следующий, пройдя по множеству произвольно малой площади; повторив эту операцию несколько раз, получим требуемый разворот.

• В конструкции Безиковича при стремлении площади фигуры к нулю её диаметр стремится к бесконечности. В 1941 году Х. Дж. Ван Альфен показал^[2], что иглу можно развернуть в фигуре сколь угодно малой площади, которая находится внутри круга с радиусом 2 + ε (для произвольного ε > 0).
• Определение множества Безиковича можно усилить, потребовав, чтобы оно содержало бесконечную прямую в каждом направлении. Такие множества нулевой меры также существуют.
  • Двойственнoe множество ${\displaystyle W}$ точек к множеству этих прямых имеет следующее свойство: любая прямая из некоторой точки ${\displaystyle x_{0}}$ проходит через ${\displaystyle W}$, но при этом для почти всех точек ${\displaystyle x}$ прямые из ${\displaystyle x}$ через точки ${\displaystyle W}$ образуют множество нулевой меры.
• Существуют односвязные подходящие (в которых можно развернуть иглу) множества с площадью меньшей, чем у фигуры, ограниченной дельтоидой.
  • Такие примеры были найдены в 1965 году. Мелвин Блум и И. Ю. Шенберг показали, что их площадь можно сделать произвольно близкой к ${\displaystyle {\tfrac {\pi }{24}}(5-2{\sqrt {2}})}$.
  • В 1971 году Каннингем показал^[3], что для любого ε > 0 существует подходящая односвязная фигура с площадью менее ${\displaystyle {\tfrac {\pi }{108}}+\varepsilon }$, содержащаяся в круге радиуса 1.

• Определим множество Безиковича в Rⁿ как множество нулевой меры, содержащее единичный отрезок в любом направлении (такое множество также называется множеством Какея, или множеством Какейя). Так называемая гипотеза Какея утверждает, что множества Безиковича имеют размерность n (по Хаусдорфу и по Минковскому), то есть равна размерности объемлющего пространства.
  • Гипотеза Какея верна в размерностях 1, 2^[4] и 3^[5].
  • Вольфф показал^[6], что в n-мерном пространстве размерность множества Безиковича должна быть по крайней мере (n+2)/2.
  • В 2002 году Кац и Тао улучшили оценку Вольффа^[7], показав, что размерность не может быть меньше ${\displaystyle (2-{\sqrt {2}})(n-4)+3}$. Эта оценка лучше для n > 4.
• Определим (n, k)-множество Безиковича как компактное множество в Rⁿ нулевой меры, содержащее в каждом k-мерном направлении k-мерный единичный диск.

  Гипотеза про (n, k)-множества Безиковича: (n, k)-множеств Безиковича не существует при k > 1.

  • В 1979 году Марстранд доказал^[8], что не существует (3, 2)-множества Безиковича.
  • Примерно в то же время, Фолкнер доказал^[9], что нет (n, k)-множеств для 2k > n.
  • Лучшая оценка на сегодня принадлежит Бургейну, который доказал^[10], что множества, у которых 2^k-1 + k > n, не существуют.
• В 1997^[11] и 1999^[12] году Вольфф доказал, что множества, содержащие сферу любого радиуса, должны иметь полную размерность, то есть размерность объемлющего пространства.
• Элиас Штайн доказал^[13], что любое множество, содержащее сферу вокруг каждой точки, должно иметь положительную меру при n ≥ 3, и Марстранд доказал^[14] то же для случая n = 2.
• В 1999 году Вольфф сформулировал аналог задачи об игле для конечных полей. Пусть F — конечное поле. Множество K ⊆ Fⁿ называется множеством Безиковича, если для каждого вектора y∈Fⁿ существует такой x∈Fⁿ, что K содержит все вектора вида {x + ty : t ∈ F}.

• Задача об игле в пространстве над конечным полем: Число элементов в K не меньше c_n|F|ⁿ, где c_n>0 — константа, которая зависит только от n.
• Двир^[15][16] доказал эту гипотезу для c_n = 1/n!, используя следующий аргумент. Двир отметил, что любой многочлен с n переменными степени менее чем |F|, который равен нулю на множестве Безиковича, должен быть тождественно равен нулю. С другой стороны, многочлены с n переменными степени менее чем |F| образуют векторное пространство размерности

${\displaystyle {|\mathbf {F} |+n-1 \choose n}\geqslant {\frac {|\mathbf {F} |^{n}}{n!}}.}$

Следовательно, существует хотя бы один нетривиальный многочлен степени меньше, чем |F|, который равен нулю на произвольном множестве с меньшим числом точек. Отсюда множество Безиковича должно иметь хотя бы |F|ⁿ/n! точек. Двир написал обзорную статью об этой задаче.^[15]

• В 1971 году Фефферман использовал^[17] построение множества Безиковича, чтобы показать, что в размерности большей, чем 1, усеченные интегралы Фурье, взятые по шарам с центром в начале координат с радиусами, стремящимися к бесконечности, могут не сходиться по норме L^p при р ≠ 2 (в отличие от одномерного случая, где такие усеченные интегралы сходятся).

• Дельтоида
• Задача Лебега
• Множество Никодима

• Яглом И. М., Болтянский В. Г. Выпуклые фигуры. — М.—Л.: ГТТИ, 1951. — 343 с. — (Библиотека математического кружка, вып. 4).
• Besicovitch, Abram (1963). «The Kakeya Problem». American Mathematical Monthly 70 (7): 697—706. doi:10.2307/2312249. JSTOR 2312249. MR 0157266.
• Dvir, Zeev (2009). «On the size of Kakeya sets in finite fields». Journal of the American Mathematical Society 22 (4): 1093—1097. arXiv: 0803.2336. doi:10.1090/S0894-0347-08-00607-3. MR 2525780.
• Falconer, Kenneth J. (1985). The Geometry of Fractal Sets. Cambridge Tracts in Mathematics 85. Cambridge: Cambridge University Press. ISBN 0-521-25694-1. MR 0867284.
• Kakeya, Soichi (1917). «Some problems on maximum and minimum regarding ovals». Tohoku science reports 6: 71-88.
• Katz, Nets Hawk; Łaba, Izabella; Tao, Terence (2000). «An improved bound on the Minkowski dimension of Besicovitch sets in ${\displaystyle \mathbf {R} ^{3}}$» (PDF). Annals of Mathematics 152 (2): 383—446. doi:10.2307/2661389. JSTOR 2661389. MR 1804528.
• Wolff, Thomas (1999). «Recent work connected with the Kakeya problem». In Rossi, Hugo. Prospects in Mathematics: Invited Talks on the Occasion of the 250th Anniversary of Princeton University. Providence, RI: American Mathematical Society. pp. 129–162. ISBN 978-0-8218-0975-4. MR 1660476.
• Wolff, Thomas (2003). Łaba, Izabella; Shubin, Carol, eds. Lectures on Harmonic Analysis. University Lecture Series 29. With a foreword by Charles Fefferman and preface by Izabella Łaba. Providence, RI: American Mathematical Society. doi:10.1090/ulect/029. ISBN 0-8218-3449-5. MR 2003254.

• The Kakeya problem, and connections to harmonic analysis at University of British Columbia.
• Besicovitch at UCLA
• Kakeya needle problem at mathworld
• An Introduction to Besicovitch-Kakeya Sets