Умножение вектора на число

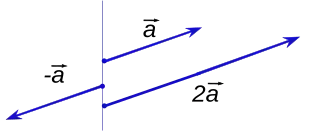
Справа исходный вектор a умножен на положительное число 2, а слева — на отрицательное число −1

Умноже́ние ве́ктора на число́, или умножение вектора на скаля́р^[1] — операция, ставящая в соответствие вектору и числу (скаляру) другой коллинеарный вектор — произведение вектора на это число^[2]. При этом произведение вектора и числа в случае ненулевых сомножителей — новый вектор, у которого^[3]^[4]^[5]:

модуль равен произведению модуля исходного вектора на абсолютную величину числа;
направление, совпадающее с направлением исходного вектора, если число положительно, и противоположное, если число отрицательно.

Обозначение произведения вектора $\mathbf {a}$ и скаляра $\lambda$ следующее^[3]^[4]^[5]:

\mathbf {a} \lambda

или

\lambda \mathbf {a} .

В итоге получаем^[3]:

|\lambda \mathbf {a} |=|\mathbf {a} \lambda |=|\lambda ||\mathbf {a} |.

Произведение вектора и числа равно нулевому вектору тогда и только тогда, когда хотя бы один из сомножителей равен нулю^[3]^[4]^[5]:

\lambda \mathbf {0} =0\mathbf {a} =\mathbf {0} .

Существуют два действия, обратных умножению вектора на число:

деление вектора на число;
деление вектора на вектор.

Определение

Умножение вектора на число — операция, ставящая в соответствие вектору и числу другой коллинеарный вектор — произведение вектора на это число^[2].

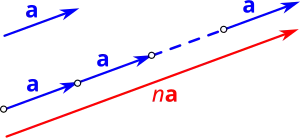
Умножение вектора a на целое положительное число n

Умножение вектора a на целое отрицательное число -n

Умножение вектора $\mathbf {a}$ на целое положительное число $n$ равно сложению вектора $\mathbf {a}$ с самим собою $n$ раз. В результате возникает новый вектор $n\mathbf {a}$ с тем же направлением, что и исходный, но в $n$ раз большим модулем^[6]^[7]:

n\mathbf {a} =\underbrace {\mathbf {a} +\mathbf {a} +\cdots +\mathbf {a} } _{n~~{\text{слагаемых}}}.

Тогда умножение вектора $\mathbf {a}$ на целое отрицательное число $-n$ равно умножению противоположного вектора $-\mathbf {a}$ на абсолютную величину целого числа $|-n|=n$ ^[8]:

(-n)\mathbf {a} =n(-\mathbf {a} ).

Другими словами, в результате возникает новый вектор $-n\mathbf {a}$ с направлением, противоположным исходному вектору $\mathbf {a}$ и в $n$ раз большим модулем^[3]^[7].

Обобщая, получаем, что произведение вектора и числа в случае ненулевых сомножителей — новый вектор, у которого^[3]^[4]^[5]:

модуль равен произведению модуля исходного вектора на абсолютную величину числа;
направление, совпадающее с направлением исходного вектора, если число положительно, и противоположное, если число отрицательно.

Обозначения произведения вектора $\mathbf {a}$ и скаляра $\lambda$ ^[3]^[4]^[5]:

\mathbf {a} \lambda

или

\lambda \mathbf {a} .

Отсюда следует, что модуль произведения вектора и скаляра равен произведению их модулей^[3]:

|\lambda \mathbf {a} |=|\mathbf {a} \lambda |=|\lambda ||\mathbf {a} |.

Произведение вектора и числа равно нулевому вектору тогда и только тогда, когда хотя бы один из сомножителей равен нулю^[3]^[4]^[5]:

\lambda \mathbf {0} =0\mathbf {a} =\mathbf {0} .

Законы умножения на скаляр

Три закона умножения вектора на скаляр те же самые, что и законы умножения чисел^[3]:

переместительности (коммутативность):

\lambda \mathbf {a} =\mathbf {a} \lambda

;

сочетательности (ассоциативность):

\lambda (\mu \mathbf {a} )=(\lambda \mu )\mathbf {a}

;

распределительности (дистрибутивность):

(\mathbf {a} +\mathbf {b} )\lambda =\mathbf {a} \lambda +\mathbf {b} \lambda

;

(\lambda +\mu )\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {a}

.

Теорема 1. Закон переместительности. Произведение вектора на число не изменяется при перестановке сомножителей^[3]:

\lambda \mathbf {a} =\mathbf {a} \lambda .

Доказательство. По определению произведение вектора на число равно произведению числа на вектор, обе эти операции тождественны^[3].

Теорема 2. Закон сочетательности для числовых множителей. Последовательное произведение вектора на несколько чисел равно произведению вектора на произведение чисел^[7]^[9]^[10]:

\lambda (\mu \mathbf {a} )=(\lambda \mu )\mathbf {a} .

Доказательство^[11]^[10]

Векторы $\lambda (\mu \mathbf {a} ),(\lambda \mu )\mathbf {a}$ обладают свойствами^[11]^[10]:

имеют одинаковые направления:

если числа $\lambda$ и $\mu$ одного знака, то оба вектора сонаправлены с вектором $\mathbf {a}$ ;
если числа $\lambda$ и $\mu$ разных знаков, то оба вектора противоположно направлены вектору $\mathbf {a}$ ;

имеют одинаковые модули:

|\lambda (\mu \mathbf {a} )|=|\lambda ||\mu \mathbf {a} |=|\lambda ||\mu ||\mathbf {a} |;

|(\lambda \mu )\mathbf {a} |=|\lambda \mu ||\mathbf {a} |=|\lambda ||\mu ||\mathbf {a} |.

Следовательно, векторы

\lambda (\mu \mathbf {a} )

и

(\lambda \mu )\mathbf {a}

равны как имеющие одинаковые направления и модули^[11]^[10].

Теорема 3. Закон двоякой распределительности. Почленно можно вычислять произведения сумм^[11]^[12]:

векторов на число (закон распределительности числового сомножителя относительно суммы векторов^[2]):

(\mathbf {a} +\mathbf {b} )\lambda =\mathbf {a} \lambda +\mathbf {b} \lambda

;

чисел на вектор (закон распределительности векторного сомножителя относительно суммы чисел^[2])^[7]:

(\lambda +\mu )\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {a}

.

Доказательство^[13]^[7]^[12]

Сумма векторов a и b, умноженных на число λ

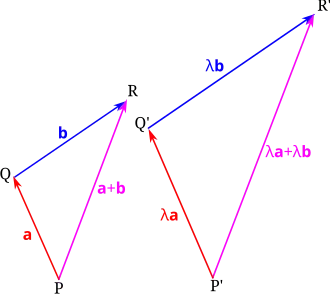
1. Построим треугольники^[11]^[7]^[12]:

$PQR$ со сторонами $\mathbf {a} ,\mathbf {b} ,\mathbf {a} +\mathbf {b}$ ;
$P'Q'R'$ со сторонами $\lambda \mathbf {a} ,\lambda \mathbf {b} ,\lambda \mathbf {a} +\lambda \mathbf {b}$ .

Эти треугольники подобны, поскольку их стороны $PQ,QR$ и $P'Q',Q'R'$ соответственно параллельны и пропорциональны^[11]^[7]^[12]:

{\frac {P'Q'}{PQ}}={\frac {Q'R'}{QR}}=\lambda

.

Следовательно, третьи стороны треугольников также параллельны и их отношение также равно $\lambda$ , то есть первый закон распределительности доказан^[13]^[7]^[12]:

\lambda \mathbf {a} +\lambda \mathbf {b} =\lambda (\mathbf {a} +\mathbf {b} )a

.

Рисунок справа сделан для положительного $\lambda$ . При отрицательном $\lambda$ направления всех трёх сторон треугольника $P'Q'R'$ меняются на противоположные и доказательство остаётся справедливым^[14].

2. Рассмотрим два случая, определяемые знаком суммы чисел $\lambda +\mu$ ^[14]^[15]:

$\lambda +\mu >0$ . Тогда векторы

(\lambda +\mu )\mathbf {a}

и

\lambda \mathbf {a} +\mu \mathbf {a}

сонаправлены и их модули равны, поскольку

|(\lambda +\mu )\mathbf {a} |=|\lambda +\mu ||\mathbf {a} |=\lambda |\mathbf {a} |+\mu |\mathbf {a} |

,

|\lambda \mathbf {a} +\mu \mathbf {a} |=\lambda |\mathbf {a} |+\mu |\mathbf {a} |

,

то есть в этом случае второй закон распределительности доказан:

(\lambda +\mu )\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {a}

;

$\lambda +\mu <0$ . Тогда $-\lambda -\mu >0$ , и по доказанному в первом случае

(-\lambda -\mu )\mathbf {a} =-\lambda \mathbf {a} +(-\mu \mathbf {a} )

.

После умножения обеих частей последнего равенства на

-1

получаем:

(\lambda +\mu )\mathbf {a} =\lambda \mathbf {a} +\mu \mathbf {a}

,

то есть и во втором случае второй закон распределительности доказан.

Доказанная формула закона распределительности числового сомножителя относительно суммы векторов

(\mathbf {a} +\mathbf {b} )\lambda =\mathbf {a} \lambda +\mathbf {b} \lambda

;

верна и для нескольких векторов^[7]:

(\mathbf {a} _{1}+\mathbf {a} _{2}+\cdots +\mathbf {a} _{n})\lambda =\mathbf {a} _{1}\lambda +\mathbf {a} _{2}\lambda +\cdots +\mathbf {a} _{n}\lambda

.

Деление векторов

Деление вектора на число

Деление вектора на число (англ. scalar division of a vector) — первая операция, обратная умножению вектора на число, ставящая в соответствие вектору и числу другой коллинеарный вектор — частное вектора и числа. Другими словами, по произведению вектора на число и числу определяется вектор-сомножитель. При этом частное $\mathbf {a$ — это второй вектор $\mathbf {b} ={\frac {\mathbf {a} }{\lambda }}$ такой, что $\lambda \mathbf {b} =\mathbf {a}$ ^[16].

Частное вектора и числа определяется умножением вектора на обратное число^[14]^[17]:

{\frac {\mathbf {a} }{\lambda }}={\frac {1}{\lambda }}\mathbf {a}

.

Деление вектора на вектор

Деление вектора на вектор (англ. vector division), причём второй вектор ненулевой, — вторая операция, обратная умножению вектора на число, ставящая в соответствие двум коллинеарным векторам, причём второй вектор ненулевой, число — частное, или отношение^[18], двух коллинеарных векторов. Другими словами, по произведению ненулевого вектора на число и второму коллинеарному вектору определяется число-сомножитель. При этом частное $\mathbf {a$ — это число $\lambda ={\frac {\mathbf {a} }{\mathbf {b} }}$ такое, что $\lambda \mathbf {b} =\mathbf {a}$ ^[19].

Частное, или отношение, ${\frac {\mathbf {a} }{\mathbf {b} }}$ двух коллинеарных векторов $\mathbf {a}$ и $\mathbf {b}$ , причём второй вектор ненулевой, вычисляется следующим образом^[19]^[20]:

$|\lambda |=\left|{\frac {\mathbf {a} }{\mathbf {b} }}\right|={\frac {|\mathbf {a} |}{|\mathbf {b} |}}$ ;
$\lambda >0$ , если векторы $\mathbf {a}$ и $\mathbf {b}$ сонаправлены, $\lambda <0$ , если векторы $\mathbf {a}$ и $\mathbf {b}$ противоположно направлены, и $\lambda =0$ , если $\mathbf {a} =\mathbf {0}$ .

Частное равных векторов равно 1. Два вектора взаимно противоположны, если их частное равно −1, тогда их можно обозначить $\mathbf {a}$ и $-\mathbf {a}$ . Частное нулевого вектора и любого другого ненулевого равно нулю. Частное любого вектора и нулевого не определено^[20]. Если ${\frac {\mathbf {a} }{\mathbf {c} }}={\frac {\mathbf {b} }{\mathbf {c} }}$ , то $\mathbf {a} =\mathbf {b}$ ^[21].

Для любых трёх векторов $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ , причём векторы $\mathbf {b}$ и $\mathbf {c}$ ненулевые, выполняется следующее равенство^[22]^[21]:

{\frac {\displaystyle {\frac {\mathbf {a} }{\mathbf {c} }}}{\displaystyle {\frac {\mathbf {b} }{\mathbf {c} }}}}={\frac {\mathbf {a} }{\mathbf {c} }}{\frac {\mathbf {c} }{\mathbf {b} }}={\frac {\mathbf {a} }{\mathbf {b} }}

.

Деление вектора на вектор используется при разложении вектора в одномерном случае^[23]^[24].

Разложение вектора

Геометрическое вычитание векторов — операция, обратная геометрическому сложению векторов. Кроме неё, обратной операцией к сложению векторов является геометрическое разложение вектора, или просто разложение вектора — операция представления данного вектора в виде замыкающей нескольких векторов. Геометрически строится ломаная линия, которую замыкает данный вектор. Но так эту операцию определить нельзя, и чтобы её определить, нужно наложить на геометрические слагаемые определённые условия, которые рассматриваются в следующих трёх разделах^[7].

Одномерный случай

Умножение вектора на положительные (синие) и отрицательные (красные) числа: частное синих векторов и чёрного вектора равны 2 и 0,5; частные красных векторов и чёрного вектора равны –1 и –0,4

Векторы Если векторы $\mathbf {a}$ и $\mathbf {b}$ связаны соотношением

\mathbf {a} =\lambda \mathbf {b}

,

то они коллинеарны. Обратное утверждение также справедливо по следующей теореме^[23].

Теорема 4. Разложение вектора по одному коллинеарному вектору. Любой вектор $\mathbf {a}$ можно единственным образом выразить через коллинеарный вектор $\mathbf {b}$ ^[23]^[24]:

\mathbf {a} =\lambda \mathbf {b}

,

где $\lambda ={\frac {\mathbf {a} }{\mathbf {b} }}$ — число, которые вычисляется так, как показано в предыдущем разделе Деление векторов.

Рассмотрим случай равенства единице модуля одного из коллинеарных векторов, то есть когда этот вектор единичный, или орт. Орт вектора $\mathbf {a}$ обозначают $\mathbf {a} ^{0}$ или $\mathbf {a} _{1}$ ^[23]^[25].

Орт вектора $\mathbf {a} ^{0}={\frac {\mathbf {a} }{|\mathbf {a} |}}$ называется также направлением вектора^[23].

Теорема 5. Любой вектор равен произведению его орта на его модуль, другими словами, умножение орта вектора на его модуль даёт сам вектор^[26]^[23]:

\mathbf {a} =|\mathbf {a} |\mathbf {a} ^{0}

.

Эта формула замечательна тем, что в ней оба элемента, которые характеризуют вектор, разделены^[23]:

модуль вектора $|\mathbf {a} |$ ;
направление вектора $\mathbf {a} ^{0}$ .

Двумерный случай

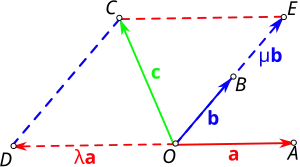
Если два вектора $\mathbf {a}$ и $\mathbf {b}$ не коллинеарны, то третий вектор — сумма векторов

\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b}

будет всегда параллелен плоскости, которую определяют векторы $\mathbf {a}$ и $\mathbf {b}$ , то есть эти три вектора компланарны, так как геометрическая сумма векторов, лежащих в одной плоскости, лежит в той же плоскости. Обратное утверждение также справедливо, как показывает следующая теорема^[23].

Теорема 6. Разложение вектора по двум неколлинеарным векторам, если все три вектора компланарны. Любой вектор $\mathbf {c}$ единственным способом выражается через неколлинеарные ненулевые векторы $\mathbf {a}$ и $\mathbf {b}$ , компланарные исходному^[23]:

\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b}

.

Доказательство^[27]

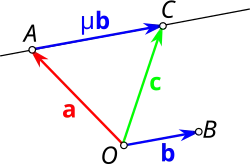
Отложим все три компланарных вектора $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ от одной и той же точки $O$ (см. рисунок справа вверху). Через конец $C$ вектора $\mathbf {c}$ проведём прямые $CE$ и $CD$ , параллельные соответственно векторам $\mathbf {a}$ и $\mathbf {b}$ , то есть соответственно прямым $OA$ и $OB$ . Тогда вектор $\mathbf {c}$ окажется геометрической суммой двух векторов $\lambda \mathbf {a}$ и $\mu \mathbf {b}$ , коллинеарных соответственно векторам $\mathbf {a}$ и $\mathbf {b}$ . В итоге получим искомое разложение вектора $\mathbf {c}$ по векторам $\mathbf {a}$ и $\mathbf {b}$ ^[23].

Докажем от противного, что это разложение единственное. Пусть имеется два разных разложения

\mathbf {c} =\lambda \mathbf {a} +\mu \mathbf {b}

,

\mathbf {c} =\lambda '\mathbf {a} +\mu '\mathbf {b}

,

тогда после вычитания этих равенств получим:

\mathbf {0} =(\lambda -\lambda ')\mathbf {a} +(\mu -\mu ')\mathbf {b}

,

откуда

\lambda -\lambda '=\mu -\mu '=0

,

то есть

\lambda =\lambda ',\quad \mu =\mu '

,

а это противоречит тому, что два исходных разложения разные^[27].

А если, например, $\lambda -\lambda '\neq 0$ , то тогда из уравнения

\mathbf {0} =(\lambda -\lambda ')\mathbf {a} +(\mu -\mu ')\mathbf {b}

следует равенство

\mathbf {a} =-{\frac {\mu -\mu '}{\lambda -\lambda '}}\mathbf {b}

,

то есть либо векторы $\mathbf {a}$ и $\mathbf {b}$ коллинеарны, либо $\mathbf {a} =\mathbf {0}$ , что противоречит условию^[28].

Теорема 7. Уравнение прямой. Уравнение прямой, проходящей через заданную точку $A$ с радиус-вектором $\mathbf {a} ={\overrightarrow {OA}}$ и параллельной заданному вектору $\mathbf {b} ={\overrightarrow {OB}}$ , задаётся следующим радиус-вектором произвольной точки прямой $C$ ^[29]:

{\overrightarrow {OC}}=\mathbf {c} =\mathbf {a} +\mu \mathbf {b}

.

Другими словами, радиус-вектор ${\overrightarrow {OC}}=\mathbf {c}$ произвольной точки $C$ заданной прямой (относительно произвольной фиксированной точки $O$ ) разлагается на сумму радиус-вектора $\mathbf {a} ={\overrightarrow {OA}}$ заданной точки $A$ прямой и направляющего вектора $\mathbf {b}$ прямой с числовым коэффициентом $\mu$ .

Доказательство. Рассмотрим вектор ${\overrightarrow {AC}}$ :

{\overrightarrow {AC}}=\mathbf {c} -\mathbf {a} =\mu \mathbf {b}

,

следовательно, вектор ${\overrightarrow {AC}}$ коллинеарен вектору $\mathbf {b}$ , и точка $C$ всегда находится на прямой, параллельной вектору $\mathbf {b}$ и проходящей через точку $A$ ^[29].

Трёхмерный случай

Теорема 8. Разложение вектора по трём некомпланарным векторам. Любой вектор $\mathbf {d}$ трёхмерного пространства единственным способом выражается через некомпланарные ненулевые векторы $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$ ^[28]^[30]:

\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c}

.

Координаты вектора — числовые коэффициенты $\lambda ,\mu ,\nu$ вектора $\mathbf {d}$ относительно $\mathbf {a} ,\mathbf {b} ,\mathbf {c}$ ^[31].

Доказательство^[28]^[32]

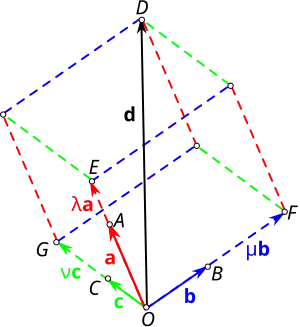
Доказательство 1. Используется правило параллелепипеда сложения векторов. Отложим все четыре вектора $\mathbf {a}$ , $\mathbf {b}$ , $\mathbf {c}$ и $\mathbf {d}$ от одной и той же точки $O$ . Через конец $D$ вектора $\mathbf {d}$ проведём три плоскости, параллельные граням трёхгранного угла, образованного тремя некомпланарными векторами $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ . Тогда $\mathbf {d}$ есть геометрическая сумма $\lambda \mathbf {a}$ , $\mu \mathbf {b}$ и $\nu \mathbf {c}$ , коллинеарных соответственно $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ . Имеем искомое разложение вектора $\mathbf {d}$ по векторам $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ ^[28].

Это разложение единственное. От противного. Пусть имеется два разных разложения

\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c}

,

\mathbf {d} =\lambda '\mathbf {a} +\mu '\mathbf {b} +\nu '\mathbf {c}

,

после вычитания:

\mathbf {0} =(\lambda -\lambda ')\mathbf {a} +(\mu -\mu ')\mathbf {b} +(\nu -\nu ')\mathbf {c}

,

откуда

\lambda -\lambda '=\mu -\mu '=\nu -\nu '=0

,

то есть

\lambda =\lambda ',\quad \mu =\mu ',\quad \nu =\nu '

,

а это противоречит тому, что два исходных разложения разные^[28].

А если, например, $\lambda -\lambda '\neq 0$ , то тогда из

\mathbf {0} =(\lambda -\lambda ')\mathbf {a} +(\mu -\mu ')\mathbf {b} +(\nu -\nu ')\mathbf {c}

следует

\mathbf {a} =-{\frac {\mu -\mu '}{\lambda -\lambda '}}\mathbf {b} -{\frac {\nu -\nu '}{\lambda -\lambda '}}\mathbf {c}

,

то есть либо векторы $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ компланарны, либо $\mathbf {a} =\mathbf {0}$ , что противоречит условию^[28].

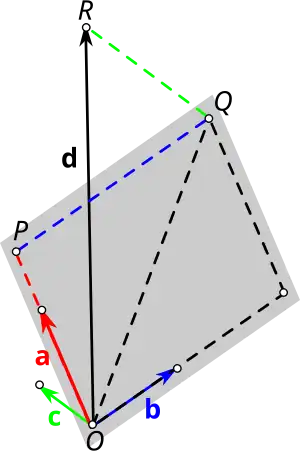
Доказательство 2. Используется правило многоугольника сложения векторов. Отложим все четыре вектора $\mathbf {a}$ , $\mathbf {b}$ , $\mathbf {c}$ и $\mathbf {d}$ от одной и той же точки $O$ . Через конец $R$ вектора $\mathbf {d}$ проведём прямую, параллельную вектору $\mathbf {c}$ и пересекающуюся с плоскостью векторов $\mathbf {a}$ и $\mathbf {b}$ в точке $\mathbf {Q}$ . Через $\mathbf {Q}$ проведём ещё одну прямую, параллельную $\mathbf {b}$ и пересекающуюся с прямой вектора $\mathbf {a}$ в точке $\mathbf {P}$ . Получаем, что

\mathbf {d} ={\overrightarrow {OP}}+{\overrightarrow {PQ}}+{\overrightarrow {QR}}

,

но ${\overrightarrow {OP}}$ , ${\overrightarrow {PQ}}$ и ${\overrightarrow {QR}}$ коллинеарны соответственно $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ , следовательно,

{\overrightarrow {OP}}=\lambda \mathbf {a}

,

{\overrightarrow {PQ}}=\mu \mathbf {b}

и

{\overrightarrow {QR}}=\nu \mathbf {c}

,

откуда

\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c}

,

что и требовалось получить^[32].

Пусть имеется два разложения

\mathbf {d} =\lambda \mathbf {a} +\mu \mathbf {b} +\nu \mathbf {c}

,

\mathbf {d} =\lambda '\mathbf {a} +\mu '\mathbf {b} +\nu '\mathbf {c}

,

после вычитания:

\mathbf {0} =(\lambda -\lambda ')\mathbf {a} +(\mu -\mu ')\mathbf {b} +(\nu -\nu ')\mathbf {c}

,

но поскольку $\mathbf {a}$ , $\mathbf {b}$ и $\mathbf {c}$ некомпланарны по условию, то

\lambda -\lambda '=\mu -\mu '=\nu -\nu '=0

,

то есть

\lambda =\lambda ',\quad \mu =\mu ',\quad \nu =\nu '

,

следовательно, оба разложения совпадают между собой^[30].

Примечания

↑ Перевод на англ. см. в закладке «Обсуждение» статьи
1 2 3 4 Умножение вектора на число, 1984.
1 2 3 4 5 6 7 8 9 10 11 12 Лаптев Г. Ф., 1975, с. 23.
1 2 3 4 5 6 Пытьев Ю. П. Векторная алгебра, 1977, с. 633.
1 2 3 4 5 6 Пытьев Ю. П. Векторная алгебра, 1988, с. 108.
↑ Лаптев Г. Ф., 1975, с. 22.
1 2 3 4 5 6 7 8 9 10 Кочин Г. Ф., 1965, с. 11.
↑ Лаптев Г. Ф., 1975, с. 22—23.
↑ Лаптев Г. Ф., 1975, с. 23—24.
1 2 3 4 Атанасян Л. С. и др., 2014, с. 219.
1 2 3 4 5 6 Лаптев Г. Ф., 1975, с. 24.
1 2 3 4 5 Атанасян Л. С. и др., 2014, с. 219—220.
1 2 Лаптев Г. Ф., 1975, с. 24—25.
1 2 3 Лаптев Г. Ф., 1975, с. 25.
↑ Атанасян Л. С. и др., 2014, с. 220.
↑ Выгодский М. Я., 1977, с. 123.
↑ Выгодский М. Я., 1977, , с. 123.
↑ Александров П. С., 1968, с. 18.
1 2 Выгодский М. Я., 1977, с. 124.
1 2 Александров П. С., 1968, с. 19.
1 2 Постников М. М., 1973, с. 27.
↑ Александров П. С., 1968, с. 20.
1 2 3 4 5 6 7 8 9 10 Кочин Г. Ф., 1965, с. 12.
1 2 Лаптев Г. Ф., 1975, с. 27.
↑ Лаптев Г. Ф., 1975, с. 26.
↑ Лаптев Г. Ф., 1975, с. 26.
1 2 Кочин Г. Ф., 1965, с. 12—13.
1 2 3 4 5 6 Кочин Г. Ф., 1965, с. 13.
1 2 Кочин Г. Ф., 1965, с. 15.
1 2 Лаптев Г. Ф., 1975, с. 30.
↑ Лаптев Г. Ф., 1975, с. 31.
1 2 Лаптев Г. Ф., 1975, с. 29—30.

Источники

Александров П. С. Лекции по аналитической геометрии, пополненные необходимыми сведениями из алгебры с приложением собрания задач, снабжённых решениями, составленного А. С, Пархоменко. 2-е изд. М.: «Наука», 1968. 912 с., ил.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б., Позняк Э. Г., Юдина И. И. Геометрия. 7—9 классы : учебник для общеобразовательных организаций. 2-е изд. М.: «Просвещение», 2014. 383 с., ил.
Выгодский М. Я. Справочник по высшей математике. Изд-е 12-е, стереотип. М.: «Наука», 1977. 871 с., ил.
Кочин Г. Ф. Векторное исчисление и начала тензорного исчисления. Изд-е 9-е. М.: «Наука», 1965. 427 с., ил.
Лаптев Г. Ф. Элементы векторного исчисления. М.: «Наука», 1975. 336 с., ил.
Постников М. М. Аналитическая геометрия. М.: «Наука», 1973. 751 с., ил.
Пытьев Ю. П. Векторная алгебра // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 1 А—Г. М.: «Советская энциклопедия», 1977. 1152 стб., ил. Стб. 632—636.
Пытьев Ю. П. Векторная алгебра // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 107—109.
Умножение вектора на число // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: «Высшая школа», 1984. 527 с., ил. С. 462.

[англ-1] Перевод на англ. см. в закладке «Обсуждение» статьи

[_d95ed1a8862e7195-2] 1 2 3 4 Умножение вектора на число, 1984.

[_0c171d2e27ea5295-3] 1 2 3 4 5 6 7 8 9 10 11 12 Лаптев Г. Ф., 1975, с. 23.

[_2916aa97312431c1-4] 1 2 3 4 5 6 Пытьев Ю. П. Векторная алгебра, 1977, с. 633.

[_bf8a2e09e8237a78-5] 1 2 3 4 5 6 Пытьев Ю. П. Векторная алгебра, 1988, с. 108.

[_00efba2e20e534ae-6] Лаптев Г. Ф., 1975, с. 22.

[_79f9838c88cfe540-7] 1 2 3 4 5 6 7 8 9 10 Кочин Г. Ф., 1965, с. 11.

[_b0d00de0c521954f-8] Лаптев Г. Ф., 1975, с. 22—23.

[_78a7e3df7b462957-9] Лаптев Г. Ф., 1975, с. 23—24.

[_05d308df02a2ecee-10] 1 2 3 4 Атанасян Л. С. и др., 2014, с. 219.

[_3400842e3d8f22cc-11] 1 2 3 4 5 6 Лаптев Г. Ф., 1975, с. 24.

[_d3bea98bef0c7d6c-12] 1 2 3 4 5 Атанасян Л. С. и др., 2014, с. 219—220.

[_cf8f9a8b7fe8c75b-13] 1 2 Лаптев Г. Ф., 1975, с. 24—25.

[_3e6b972e43f5f5b3-14] 1 2 3 Лаптев Г. Ф., 1975, с. 25.

[_1111e7c7157d598e-15] Атанасян Л. С. и др., 2014, с. 220.

[_e5825bf6818cce08-16] Выгодский М. Я., 1977, с. 123.

[_d02bf8dd9afcbb04-17] Выгодский М. Я., 1977, , с. 123.

[_49e46e4fe67ea4ce-18] Александров П. С., 1968, с. 18.

[_fea54cf68f8c00c9-19] 1 2 Выгодский М. Я., 1977, с. 124.

[_550dd14fed8728b5-20] 1 2 Александров П. С., 1968, с. 19.

[_ab2957a7cd193449-21] 1 2 Постников М. М., 1973, с. 27.

[_d2b1a26827b7ab25-22] Александров П. С., 1968, с. 20.

[_758e888c878227fd-23] 1 2 3 4 5 6 7 8 9 10 Кочин Г. Ф., 1965, с. 12.

[_2f97892e3c44c979-24] 1 2 Лаптев Г. Ф., 1975, с. 27.

[_75cb5166fe7ad140-25] Лаптев Г. Ф., 1975, с. 26.

[_2547a62e35f510f2-26] Лаптев Г. Ф., 1975, с. 26.

[_b87720191f5542bd-27] 1 2 Кочин Г. Ф., 1965, с. 12—13.

[_6b40a58c8135d376-28] 1 2 3 4 5 6 Кочин Г. Ф., 1965, с. 13.

[_9d77ef8c9d26f754-29] 1 2 Кочин Г. Ф., 1965, с. 15.

[_c838a4371e980189-30] 1 2 Лаптев Г. Ф., 1975, с. 30.

[_c3db41371d55cfc2-31] Лаптев Г. Ф., 1975, с. 31.

[_3d7196f61f029d30-32] 1 2 Лаптев Г. Ф., 1975, с. 29—30.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]