Неравенство Коши для аналитической функции
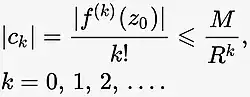
Нера́венство Коши́[1] — понятие комплексного анализа, раздела математики, неравенство в фиксированной точке комплексной плоскости для модуля производной аналитической функции или для модуля коэффициента разложения этой функции в степенной ряд или в ряд Лорана[2][3][4][5].
Значение неравенств Коши, играющих существенную роль в теории функций комплексного переменного, состоит в том, что они оценивают производные аналитических функций, хотя и завышенные, используя лишь значение максимума модуля функции[6].
|
Теорема (неравенство Коши). Если аналитическая функция в замкнутом круге радиуса (в открытом кольце) комплексной плоскости имеет максимум своего модуля на границе круга — окружности радиуса (соответственно на любой концентрической окружности радиуса открытого кольца), то модуль любой -й производной не превышает числа в центре круга (соответственно в любой точке указанной окружности), а -й коэффициент ряда Тейлора функции (соответственно ряда Лорана функции) не превышает числа в центре круга (соответственно в любой точке указанной окружности)[2][3][4][5]. |
Замечание. Условие аналитичности функции в замкнутом круге можно заменит на более слабое условие аналитичности функции в открытом круге и её непрерывности в замкнутом круге (аналогичный случай более слабого условия возникает при формулировке леммы Чеботарёва)[3].
Под неравенствами Коши могут понимать только неравенства Коши для производных аналитических функций[7], поскольку любой сходящийся на комплексной плоскости степенной ряд есть ряд Тейлора своей суммы[8][9][10]:
Поэтому неравенства Коши можно записать в виде следующей одной формулы[10]:
Неравенства Коши
Под неравенствами Коши могут понимать только неравенства Коши для производных аналитических функций[7], поскольку любой сходящийся на комплексной плоскости степенной ряд есть ряд Тейлора своей суммы[8]:
Поэтому неравенства Коши можно записать в виде следующей одной формулы[10]:
Неравенства Коши для производных аналитических функций
|
Теорема (неравенства Коши для производных аналитических функций). Дано: аналитическая функция в открытом круге (имеющем радиус и центр ) комплексной плоскости , непрерывная в замкнутом круге . Доказать: все производные от функции в точке удовлетворяют неравенствам где — максимальное значение модуля функции на окружности [3][11][12][7]. |
Замечание. Условие аналитичности функции в открытом круге и её непрерывности в замыкании круга можно заменит на более простое, но и более сильное условие аналитичности функции в замкнутом круге[4].
Доказательство. По интегральной формуле Коши
- ,
где — окружность . После оценки этого интеграла получается искомые неравенства Коши[13][11][7]:
- .
Замечание. Эта теорема говорит о том, что увеличение значений производных аналитической функции при не произволен, поскольку связан с расстоянием до границы области аналитичности[13].
Неравенства Коши для коэффициентов ряда Тейлора
Синоним: неравенства Коши для коэффициентов степенного ряда[14].
|
Теорема 1 (неравенства Коши для коэффициентов ряда Тейлора[15]). Дано: аналитическая функция в замкнутом круге комплексной плоскости , модуль которой не больше вещественного числа на окружности . Доказать: коэффициенты ряда Тейлора функции с центром в точке удовлетворяют следующим неравенствам[4][16][17][18][19]: |
Замечание. Условие аналитичности функции в замкнутом круге можно заменит на более слабое условие аналитичности функции в открытом круге и её непрерывности на границе круга[3].
Доказательство. По интегральной формуле Коши
откуда при для всех точек получаем следующие неравенства[4][20][17][18][19]:
- □
Альтернативная формулировка теоремы состоит в следующем[7].
|
Теорема 2 (неравенства Коши для коэффициентов ряда Тейлора[15]). Дано: Пусть степенной ряд сходится абсолютно в окрестности некоторой точки . Доказать: для достаточно малого верно следующее неравенство[7]: |
Доказательство. Неравенство получается при использовании неравенств Коши для производных аналитических функций[7]. □
Неравенства Коши для коэффициентов ряда Лорана
|
Теорема (неравенства Коши для коэффициентов ряда Лорана). Дано: аналитическая функция в открытом кольце комплексной плоскости , модуль которой не больше вещественного числа на окружности , . Доказать: коэффициенты ряда Лорана функции в кольце удовлетворяют следующим неравенствам[5][21][22][23][24][25]: |
Доказательство 1. По интегральной формуле Коши
откуда при для всех точек получаем следующие неравенства[15][22][23][24][26]:
- □
Эту теорему можно также доказать напрямую, без использования интегральной формулы Коши[27].
1. Случай . Сначала докажем требуемое неравенство
для случая . Рассмотрим ряд Лорана
- ,
где
- ,
- .
Так как степенные ряды и равномерно сходятся на окружности , для произвольного найдём такое число , что в равенстве
для функции выполняется неравенство для любых точек окружности .
То есть для функции (штрих над суммой пропускает член с номером 0)
для любых точек окружности верно неравенство
- .
1.1. Число . Подберём число , имеющее модуль и отличные от нуля целые степени, не равные . (Существование таких чисел будет показано в п. 2.1.) Пусть — произвольное натуральное число, тогда все точки
принадлежат окружности . Тогда имеем равенство
- .
Отсюда
- ,
где величина
не зависит от выбранного произвольного натурального числа . Далее получаем:
- .
Так как число как угодно велико, а число как угодно мало, то
- ,
и тем самым требуемое неравенство доказано для случая
2. Случай произвольного . Рассмотрим детально ряд
В этом ряде коэффициент , причём на окружности
- .
Учитывая, что раньше было , имеем: .
Требуемое неравенство доказано в полном объёме.
2.1. Число . Одним из чисел является число
- .
В самом деле, имеем, что , и предположим, что имеется такое натуральное , что . Тогда
-
- ,
то есть
- ,
где и — целые вещественные числа. Отсюда получаем:
- ,
- ,
которое противоречиво, поскольку никак не может делится на . Это противоречие говорит о том, что ни при каком натуральном, а следовательно, и целом , отличном от нуля.
Более точные оценки
Значение неравенств Коши состоит в том, что они оценивают производные аналитических функций, хотя и завышенные, используя лишь значение максимума модуля функции [28].
Оценка, даваемые неравенствами Коши
при заданных числах и , зависит от значения радиуса , который произволен в пределах , где — расстояние от точки комплексной плоскости до границы области аналитичности функции [29].
Для наиболее точной оценки находят минимум функции и выбирают именно такой радиус , при котором функция достигает своего минимума[29].
Пример 1. Пусть: 1) область аналитичности функции — это единичный открытый круг ; 2) точка комплексной плоскости , где осуществляется оценка производных, — это центр этого круга; 3) функция отвечает следующему неравенству[29]:
- .
Тогда из неравенства
получаем следующее более конкретное неравенство[29]:
Для получения самой лучшей оценки найдём минимум функции , другими словами, найдём максимум функции в интервале . Используя стандартные правила дифференциального исчисления:
- ,
получаем, что искомый экстремум достигается при радиусе и равен следующей величине[28]:
Окончательно получаем[28]:
Пример 2. Рассмотрим частный случай примера 1, когда исходная функция имеет следующий вид[28]:
- .
Эта функция аналитическая в единичном круге, причём для этой функции [28].
В итоге непосредственные вычисления дают следующие равенства[28]:
Обобщения неравенств Коши
Усиление неравенств Коши
1. Ряд Тейлора. Рассмотрим некоторое усиление неравенств Коши, сначала для ряда Тейлора[26].
|
Теорема 1 (интегральное среднее от квадрата модуля аналитической функции). Дано: Ряд Тейлора аналитической функции
сходящийся в открытом круге . Доказать: для любых радиусов интегральное среднее от квадрата модуля функции по окружности радиуса равно следующей сумме квадратов модулей членов ряда Тейлора на данной окружности[30]:
|
Доказательство. Представим в следующем виде[30]:
- .
Запишем иначе разность , получим[30]:
- .
Перемножим ряды в правой части равенства и проинтегрируем равенство почленно по окружности при [30]:
-
- .
Поскольку, по интегральной теореме Коши, интегралы по окружности от аналитических членов ряда с равны нулю, окончательно имеем[30]:
- . □
|
Теорема 2 (усиление неравенств Коши). Дано: условие предыдущей теоремы. Доказать: верно следующее неравенство[30]: |
Доказательство. По предыдущей теореме получаем[30]:
- . □
|
Теорема 3 (равенство Коши). Дано: Ряд Тейлора аналитической функции
сходящийся в открытом круге , причём хотя бы одно из неравенств Коши обращается в равенство, то есть существуют такие и , что . Доказать:
где — некоторая константа[30]. |
Доказательство. По усиленному неравенству Коши для указанного
- ,
следовательно,
поэтому
- ,
где [30]. □
Следствие. Сразу два разные неравенства Коши суть равенства тогда и только тогда, когда [30].
2. Ряд Лорана. Теперь приведём усиление неравенств Коши для ряда Лорана[26].
|
Теорема 4 (интегральное среднее от квадрата модуля аналитической функции). Дано: Ряд Лорана аналитической функции
сходящийся в открытом кольце . Доказать: для любых радиусов интегральное среднее от квадрата модуля функции по окружности радиуса равно следующей сумме квадратов модулей членов ряда Лорана на данной окружности[26]:
|
Доказательство. Доказательство совпадает с доказательством аналогичной теоремы для ряда Тейлора[26].
|
Теорема 5 (усиление неравенств Коши). Дано: условие предыдущей теоремы. Доказать: верно следующее неравенство[26]: |
Доказательство. Доказательство совпадает с доказательством аналогичной теоремы для ряда Тейлора[26].
|
Теорема 6 (равенство Коши). Дано: Ряд Лорана аналитической функции
сходящийся в открытом кольце , причём хотя бы одно из неравенств Коши обращается в равенство, то есть существуют такие и , что . Доказать:
где — некоторая константа[26]. |
Доказательство. Доказательство совпадает с доказательством аналогичной теоремы для ряда Тейлора[26].
Модификация неравенств Коши
|
Теорема (модификация неравенств Коши). Дано: аналитическая функция в открытом круге комплексной плоскости , а действительная часть этой функции на окружности , . Доказать: коэффициенты ряда Тейлора функции в открытом круге удовлетворяют следующим неравенствам[31]: |
При и по формуле Шварца имеем:
- ,
и поскольку при
- ,
то, подставляя эту формулу в предыдущую и почленно интегрируя, получаем:
- , .
Поскольку при целых
- ,
то, вычитая из этого равенства предыдущее, получаем следующее равенство:
- , .
А так как по условию теоремы при любых , , то, осуществляя переход к модулям и учитывая теорему о среднем для гармонических функций , окончательно имеем:
- , .
Неравенство Коши — Адамара
Значение неравенств Коши состоит в том, что они оценивают производные аналитических функций, хотя и завышенные, используя лишь значение максимума модуля функции [28].
Неравенства Коши непосредственно приводят к следующей теореме[2][28].
|
Теорема (неравенство Коши — Адамара). Дано: аналитическая функция в открытом круге (имеющем радиус и центр ) комплексной плоскости , непрерывная в замкнутом круге . Доказать: неравенство для предела где — расстояние от точки комплексной плоскости до границы области аналитичности функции [2][28]. |
Доказательство. Доказательство основано на неравенствах Коши для производных аналитических функций. Зафиксируем в этих неравенствах радиус и извлечём из обеих частей неравенств корень степени [28]:
Поскольку , то получаем следующие неравенства для верхних пределов[28]:
- .
Учитывая, что в последних неравенствах радиус — произвольное положительное число, то перейдём к пределу при , окончательно имеем[28]:
- . □
Неравенство Коши — Адамара говорит о том, что величина оценки
- ,
которая зависит от значений производных аналитических функций в некоторой точке , связана обратной зависимостью с расстоянием точки до границы области, а именно: эта величина оценки не может быть большой при большом расстоянии до границы, там, где граница области аналитически далека от точки [32].
Следствие. Если функция целая, то в произвольной точке верно следующее равенство[2][33]:
- .
Доказательство. Для целых функций, аналитических во всей комплексной плоскости, единственная граничная точка области находится в бесконечности, поэтому для любой точки плоскости расстояние , то есть [33]. □
Пример. Рассмотрим функцию . При любом имеем: , поэтому . Для целой части получаем[33]:
- ,
- ,
следовательно,
- при .
Обобщение на комплексное пространство
Неравенства Коши для комплексного пространства доказываются аналогично неравенствам Коши для комплексной плоскости. Сформулируем одну из теорем неравенств Коши — о неравенствах Коши для производных аналитических функций — для случая нескольких комплексных переменных[34][2][35][36][37][38][39][10][7].
|
Теорема (неравенства Коши для производных аналитических функций. Дано: аналитическая функция в открытом поликруге векторного радиуса комплексного пространства , непрерывная в замкнутом поликруге векторного радиуса , модуль которой не больше вещественного числа на остове поликруга . Доказать: все производные от функции в точке удовлетворяют следующим неравенствам[34][2][35][36][38][39][10][7]: |
Неравенства Коши можно записать в виде следующей одной формулы[10]:
- .
Примечания
- ↑ Перевод на англ. см. в закладке «Обсуждение» статьи
- 1 2 3 4 5 6 7 Соломенцев Е. Д. Коши неравенство. 2), 1982.
- 1 2 3 4 5 Соломенцев Е. Д. Функции комплексного переменного и их применения, 1988, § 14. Интегральная формула Коши…, с. 48—49.
- 1 2 3 4 5 Шабат Б. В. Введение в комплексный анализ, ч. I, 1976, 20. Ряды Тейлора, с. 108.
- 1 2 3 Шабат Б. В. Введение в комплексный анализ, ч. I, 1976, 24. Ряды Лорана, с. 132—133.
- ↑ Маркушевич А. И. Теория аналитических функций. Том I, 1967, Глава третья. Интегралы и степенные ряды. § 3. Интеграл Коши. Формулы Ю. В. Сохоцкого, с. 245—246.
- 1 2 3 4 5 6 7 8 9 Steven G. Krantz. Function Theory of Several Complex Variables, 2001, 2.3.1 Complexification, p. 104.
- 1 2 Шабат Б. В. Введение в комплексный анализ, ч. I, 1976, 21. Свойства голоморфных функций, с. 114.
- ↑ Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава II. Основные факты…. § 1. Функции комплексных переменных, с. 47.
- 1 2 3 4 5 6 Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 1.7 Limits of holomorphic functions, p. 14.
- 1 2 Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного, 1973, 17. Высшие производные, с. 64.
- ↑ Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа. Часть 1, 1963, 5.23. Неравенство Коши…, с. 130.
- 1 2 Соломенцев Е. Д. Функции комплексного переменного и их применения, 1988, § 14. Интегральная формула Коши…, с. 49.
- ↑ Привалов И. И. Введение в теорию функций комплексного переменного, 2009, Глава V. Ряды аналитических функций… § 2. Ряд Тейлора, с. 207.
- 1 2 3 Шабат Б. В. Введение в комплексный анализ, ч. I, 1976, 24. Ряды Лорана, с. 132.
- ↑ Привалов И. И. Введение в теорию функций комплексного переменного, 2009, Глава V. Ряды аналитических функций… § 2. Ряд Тейлора, с. 207—208.
- 1 2 Стоилов С. Теория функций комплексного переменного. Том I, 1962, Глава III. Дифференциальная теория голоморфности. § 3. Теория Коши. 46. Неравенства Коши. Приложения, с. 125.
- 1 2 Картан А. Элементарна теория аналитических функций одного и нескольких комплексных переменных, 1963, Глава III. Ряды Тейлора и Лорана…. § 1. Неравенство Коши; теорема Лиувилля, с. 103.
- 1 2 Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Первое полугодие, 2004, 6.3. Неравенства Коши, с. 67.
- ↑ Привалов И. И. Введение в теорию функций комплексного переменного, 2009, Глава V. Ряды аналитических функций… § 2. Ряд Тейлора, с. 208.
- ↑ Гурвиц А., Курант Р. Теория функций, 1968, § 9. Ряды Лорана, с. 47.
- 1 2 Сидоров Ю. В., Федорюк М. В., Шабунин М. И. Лекции по теории функций комплексного переменного, 1989, § 17. Ряд Лорана, с. 125—126.
- 1 2 Фукс Б. А., Шабат Б. В. Функции комплексного переменного и некоторые приложения, 1964, 64. Ряды Лорана, с. 245.
- 1 2 Половинкин Е. С. Курс лекций по теории функций комплексного переменного, 1999, § 11. Ряд Лорана, с. 84—85.
- ↑ Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Первое полугодие, 2004, 7.3. Неравенства Коши для коэффициентов Лорана, с. 86—87.
- 1 2 3 4 5 6 7 8 9 Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Первое полугодие, 2004, 7.3. Неравенства Коши для коэффициентов Лорана, с. 87.
- 1 2 Гурвиц А., Курант Р. Теория функций, 1968, § 9. Ряды Лорана, с. 47—49.
- 1 2 3 4 5 6 7 8 9 10 11 12 Маркушевич А. И. Теория аналитических функций. Том I, 1967, Глава третья. Интегралы и степенные ряды. § 3. Интеграл Коши. Формулы Ю. В. Сохоцкого, с. 246.
- 1 2 3 4 Маркушевич А. И. Теория аналитических функций. Том I, 1967, Глава третья. Интегралы и степенные ряды. § 3. Интеграл Коши. Формулы Ю. В. Сохоцкого, с. 245.
- 1 2 3 4 5 6 7 8 9 10 Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Первое полугодие, 2004, 6.5. Множество точек сходимости степенного ряда, с. 72.
- 1 2 Шабат Б. В. Введение в комплексный анализ, ч. I, 1976, 24. Ряды Лорана, с. 305—306.
- ↑ Маркушевич А. И. Теория аналитических функций. Том I, 1967, Глава третья. Интегралы и степенные ряды. § 3. Интеграл Коши. Формулы Ю. В. Сохоцкого, с. 246—247.
- 1 2 3 Маркушевич А. И. Теория аналитических функций. Том I, 1967, Глава третья. Интегралы и степенные ряды. § 3. Интеграл Коши. Формулы Ю. В. Сохоцкого, с. 247.
- 1 2 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 5. Простейшие свойства голоморфных функций, с. 31.
- 1 2 Эрве М. Функции многих комплексных переменных, 1965, Глава I. Основные свойства голоморфных функций многих переменных. 3, с. 12.
- 1 2 Хёрмандер, Ларс. Введение в теорию функций нескольких комплексных переменных, 1968, 2.2. Применение интегральной формулы Коши для поликруга, с. 48.
- ↑ Фукс Б. А. Теория аналитических функций многих комплексных переменных, 1962, § 3. Представление голоморфного функционального элемента степенным рядом, с. 62.
- 1 2 Мальгранж Б. Лекции по теории функций нескольких комплексных переменных, 1969, § 1. Формула Коши и элементарные следствия, с. 8—9.
- 1 2 Белошапка В. К. Курс лекций по комплексному анализу, 2005, 2.2.6. Стандартные теоремы о голоморфных функциях, с. 13.
Источники
- Белошапка В. К. Курс лекций по комплексному анализу. М., 2005. 31 с., ил.
- Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
- Гурвиц А., Курант Р. Теория функций / Пер. М. А. Евграфова. М.: «Наука», 1968. 648 с.: ил. [Adolf Hurwitz. Allhemeine Funktionentheorie und elliptische Funktionen. R. Courant. Geometrische Funktionentheorie. Berlin · Göttingen · Heidelberg · New York: Springer-Verlag, 1964.]
- Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Первое полугодие. М.: МИАН, 2004. 175 с.: ил. ISBN 5-98419-007-9 (ч. I). ISBN 5-98419-006-0.
- Картан, А. Элементарна теория аналитических функций одного и нескольких комплексных переменных / Пер. под ред. Б. В. Шабата. М.: «Издательство иностранной литературы», 1963. 296 с.: ил.
- Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. Изд. 4-е, испр. М.: «Наука», 1973. 736 с., 231 рис.
- Мальгранж Б. Лекции по теории функций нескольких комплексных переменных. М.: «Наука», 1969. 119 с.: ил.
- Маркушевич А. И. Теория аналитических функций. Том I. Начала теории. Издание второе. М.: «Наука», 1967. 486 с.: ил.
- Половинкин Е. С. Курс лекций по теории функций комплексного переменного. М.: МФТИ, 1999. 253 с.: ил. ISBN 5-7417-0129-9.
- Привалов И. И. Введение в теорию функций комплексного переменного : учебник. 15-е изд., стер. СПб.: Лань, 2009. 432 с.: ил. ISBN 978-5-8114-0913-6.
- Сидоров Ю. В., Федорюк М. В., Шабунин М. И. Лекции по теории функций комплексного переменного: Учеб. для вузов. 3-е изд., испр. М.: «Наука», 1989. 477 с. ISBN 5-02-013954-8.
- Соломенцев Е. Д. Коши неравенство // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 3 Коо—Од. М.: «Советская Энциклопедия», 1982. 1184 стб., ил. Стб. 59.
- Соломенцев Е. Д. Функции комплексного переменного и их применения: Учеб. пособие для студентов вузов. М.: «Высшая школа», 1988. 167 с., ил. ISBN 5-06-003145-6.
- Стоилов С. Теория функций комплексного переменного. Том I. Основные понятия и принципы: Пер. с румынского И. Берштейна. Ред. Е. Д. Соломенцев. М.: «Издательство иностранной литературы», 1962. 364 с., ил. [Stoilow S. Teoria Funcțiilor de o Variabilǎ Complexǎ, vol. I Noțiuni și Principii Dundamentale. Editura Academiei Republicii Populare Române, 1954.]
- Уиттекер Э. Т., Ватсон Дж. Н. Курс современного анализа. Часть 1. Основные операции анализа. 2-е изд. / Пер. с англ. под ред. Ф. В. Широкова. М.: Физматлит, 1963. 343 с.: ил. [Whittaker E. T., Watson G. N. A course of modern analysis. 4th edition. Cambridge: At the University Press, 1927.]
- Фукс Б. А. Теория аналитических функций многих комплексных переменных: 2-е изд., перераб. и доп. М.: Физматлит, 1962. 419 с.
- Фукс Б. А., Шабат Б. В. Функции комплексного переменного и некоторые приложения: 3-е изд. М.: «Наука», 1964. 387 с. с илл.
- Хёрмандер, Ларс. Введение в теорию функций нескольких комплексных переменных / Пер. с англ. Е. М. Чирки, под ред. Б. В. Шабата. М.: «Мир», 1968. 279 с.
- Шабат Б. В. Введение в комплексный анализ, ч. 1, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 320 с.: ил.
- Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.
- Эрве М. Функции многих комплексных переменных. Локальная теория. Пер. с англ. Б. А. Фукса. М.: «Мир», 1965. 165 с. [Hervé M. Several complex variables. Local theory. Bombay: Oxford University Press, 1963.]
- Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.
- Steven G. Krantz. Function Theory of Several Complex Variables: Second edition. Providence, Rhode Island: AMS Chelsea Publishing, 1951. 564 p. 1992 held by the American Mathematical Society. Printed with corrections, 2001.