Полуплоскость

Полупло́скость^[1] — множество всех точек плоскости, которые находятся по одну сторону от некоторой прямой на этой плоскости^[2]^[3]^[4]^[5]^[6]^[7], то есть по ту же сторону, что и некоторая заданная точка вне прямой^[6]. Эта прямая определяет полуплоскость^[5]^[8] и является её границей^[6]^[2]^[3]^[4], а полуплоскость исходит из своей границы^[9], или просто полуплоскость от границы^[10].

В некоторых источниках граница полуплоскости ей принадлежит, то есть полуплоскость замкнута^[6]^[11]^[12]. В некоторых школьных материалах открытость или замкнутость полуплоскости может быть несущественной^[13].

Замкнутая полуплоскость — полуплоскость со своей границей^[2]^[3]^[4].

Полуплоскость есть выпуклая неограниченная область как одновременно открытое множество^[14] и неограниченное выпуклое множество^[15].

Другое название замкнутой полуплоскости — односторонник, это простейший плоский выпуклый многосторонник^[16].

Для двумерной гиперболической геометрии (геометрии Лобачевского) построена модель Пуанкаре с метрикой Пуанкаре верхней полуплоскости^[1]^[17].

Полуплоскость, обобщение полупрямой и частный случай полупространства, обладает по сравнение с ними следующей особенностью: полуплоскость может быть комплексной^[2]^[3]^[4].

На комплексной плоскости верхняя полуплоскость имеет следующее важное свойство. Для любой точки границы единичного круга найдётся такое аналитическое отображение круга на верхнюю полуплоскость, что все преобразования с неподвижной этой точкой переходят в линейные преобразования верхней полуплоскости^[18].

Полуплоскость также есть частный случай трубчатой области^[19].

Определение полуплоскости

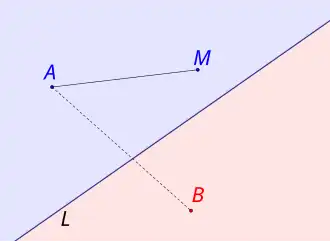
Точки $A$ и $M$ лежат в одной полуплоскости, точки $A$ и $B$ — в разных полуплоскостях с общей границей $L$

Полуплоскость $H$ — множество всех точек $M$ плоскости, которые находятся по ту же сторону от некоторой прямой $L$ на этой плоскости, что и некоторая заданная точка $A$ вне прямой, то есть полуплоскость $H$ — это точка $A$ и множество всех точек $M$ таких, что отрезок $AM$ не имеет общих точек с прямой $L$ ^[20]. Прямая $L$ определяет полуплоскость $H$ ^[5]^[8] и является её границей^[6]^[2]^[3]^[4].

Замкнутая полуплоскость ${\bar {H}}$ — полуплоскость со своей границей $\partial H$ , ${\bar {H}}=H\cup \partial H$ ^[2]^[3]^[4].

Теорема 1. Две точки $A\notin L$ и $M\notin L$ на одной плоскости лежат в одной и той же полуплоскости, которая определяется прямой $L$ , тогда и только тогда, когда $L$ не пересекается с отрезком $AM$ ^[8].

Теорема 2. Произвольная прямая $L$ на плоскости $P$ делит эту плоскость на две полуплоскости $H_{1}$ и $H_{2}$ ^[8]^[20]^[11]. Более формально: на плоскости $P$ вне прямой $L\subset P$ существуют точки $A$ и $B,$ $A,\,B\notin L$ , такие, что разные полуплоскости $H_{1}\subset P$ и $H_{2}\subset P$ , которым принадлежат эти точки, $A\in H_{1}$ , $B\in H_{2}$ , заполняют с прямой $L$ всю плоскость и имеют своими границами $L$ , то есть $H_{1}\cup H_{2}\cup L=P$ и $\partial H_{1}=\partial H_{2}=L$ ^[20]^[11].

Декартовы координаты

В общем двумерном случае на плоскости $\mathbb {R} ^{2}$ с декартовыми координатами $(x,\,y)$ координаты точек полуплоскости отвечают следующему неравенству, использующим общее уравнение прямой

L(x,\,y)=Ax+By+C>0

,

где $A,\,B,\,C$ — постоянные, причём $A$ и $B$ одновременно не равны нулю^[5]^[2]^[3]^[4].

Граница полуплоскости — прямая, определяющая полуплоскость. В определении это прямая

L(x,\,y)=Ax+By+C=0

^[2]^[3]^[4].

Комплексные координаты

На комплексной плоскости $\mathbb {C}$ с координатами $z=x+iy$ обычно рассматриваются следующие частные случаи^[2]^[3]^[4]:

верхняя полуплоскость^[1] $y=\operatorname {Im} z>0$ ,
нижняя полуплоскость^[1] $y=\operatorname {Im} z<0$ ,
левая полуплоскость^[1] $x=\operatorname {Re} z<0$ ,
правая полуплоскость^[1] $x=\operatorname {Re} z>0$ .

Все полуплоскости, граница которых проходит через начало координат, можно представить следующей формулой^[21]:

t-{\frac {\pi }{2}}<\operatorname {Arg} z<t+{\frac {\pi }{2}}

,

\,\,0\leqslant t<2\pi

.

Прямая и полуплоскость на комплексной плоскости

Рассмотрим на комплексной плоскости произвольную прямую $L\subset \mathbb {C}$ . Эта прямая определяется произвольной точкой $a\in L$ и вектором направления прямой $b\in \mathbb {C}$ , поэтому её уравнение будет следующим^[22]:

L=\{z=a+tb\colon \,b\neq 0,\,-\infty <t<\infty ,\,t\in \mathbb {R} \}.

Так как $b\neq 0$ , то уравнение прямой перепишем в следующем виде^[23]:

L=\left\{z\colon \,\operatorname {Im} {\frac {z-a}{b}}=0,\,b\neq 0\right\}.

Так как $b\in \mathbb {C}$ — направление прямой, положим $|b|=1$ . В этом случае пусть $a=0$ и рассмотрим полуплоскость

H_{0}=\left\{z\colon \,\operatorname {Im} {\frac {z}{b}}>0\right\}

,

где $b=e^{i\beta }$ . Теперь при $z=re^{i\theta }$ имеем ${\frac {z}{b}}=re^{i(\theta -\beta )}$ . Таким образом, $z$ принадлежит полуплоскости $H_{0}$ , $z\in H_{0}$ , тогда и только тогда, когда $\sin(\theta -\beta )>0$ , то есть когда $\beta <\theta <\pi +\beta$ . Следовательно, полуплоскость $H_{0}$ лежит слева от прямой $L$ , если «идти по $L$ в направлении $b$ »^[24].

Таким образом, полуплоскость

H_{a}=\left\{z\colon \,\operatorname {Im} {\frac {z-a}{b}}>0\right\}

есть параллельный перенос полупроскости $H_{0}$ на вектор $a$ , $H_{a}=a+H_{0}\equiv \{a+w\colon \,w\in H_{0}\}$ . Следовательно, полуплоскость $H_{a}$ лежит слева от прямой $L$ . Точно так же полуплоскость

K_{a}=\left\{z\colon \,\operatorname {Im} {\frac {z-a}{b}}<0\right\}

лежит справа от прямой $L$ ^[24].

Пример. Определение касательной

Рассмотрим на комплексной плоскости произвольную окружность $C\subset \mathbb {C}$ , $C=\{z\in \mathbb {C} \colon \,|z-c|=r,\,r>0,\,r\in \mathbb {R} \}.$ Возьмём на окружности $C$ произвольную точку $a$ , $a=c+re^{i\alpha }$ , и проведём через неё следующую прямую^[25]:

L_{\beta }=\left\{z\colon \,\operatorname {Im} {\frac {z-a}{b}}=0,\,b=e^{i\beta }\right\}.

Прямая $L_{\beta }$ касается окружности $C$ в точке $a$ тогда и только тогда, когда окружность $C$ полностью, кроме точки $a$ , принадлежит одной из полуплоскостей с границей $L_{\beta }$ , то есть когда для произвольной точки $z=c+re^{i\gamma }$ окружности $C$ , $\gamma \neq \alpha$ ,

\operatorname {Im} {\frac {z-a}{b}}>0\,\,

или

\,\,\operatorname {Im} {\frac {z-a}{b}}<0

,

то есть

\sin {\frac {\gamma -\alpha }{2}}\cos \left({\frac {\gamma +\alpha }{2}}-\beta \right)\neq 0

,

поскольку верна следующая цепочка равенств^[26]:

{\frac {z-a}{b}}={\frac {c+re^{i\gamma }-(c+re^{i\alpha })}{e^{i\beta }}}={\frac {e^{i\gamma }-e^{i\alpha }}{e^{i\beta }}}=

={\frac {1}{e^{i\beta }}}(\cos \gamma +i\sin \gamma -(\cos \alpha +i\sin \alpha ))=

={\frac {1}{e^{i\beta }}}\left(-2\sin {\frac {\gamma +\alpha }{2}}\sin {\frac {\gamma -\alpha }{2}}+2i\sin {\frac {\gamma -\alpha }{2}}\cos {\frac {\gamma +\alpha }{2}}\right)=

={\frac {1}{e^{i\beta }}}\left(2i\sin {\frac {\gamma -\alpha }{2}}\left(i\sin {\frac {\gamma +\alpha }{2}}+\cos {\frac {\gamma +\alpha }{2}}\right)\right)=

={\frac {1}{e^{i\beta }}}\left(2i\sin {\frac {\gamma -\alpha }{2}}e^{\frac {\gamma +\alpha }{2}}\right)=2i\sin {\frac {\gamma -\alpha }{2}}e^{{\frac {\gamma +\alpha }{2}}-\beta }=

=2i\sin {\frac {\gamma -\alpha }{2}}\left(\cos \left({\frac {\gamma +\alpha }{2}}-\beta \right)+i\sin \left({\frac {\gamma +\alpha }{2}}-\beta \right)\right)

.

Так как $\gamma \neq \alpha$ , то решением неравенства будет совокупность неравенств, состоящая из двух систем неравенств:

1)

{\frac {\gamma -\alpha }{2}}\neq 0

,

\,\,\left({\frac {\gamma +\alpha }{2}}-\beta \right)\neq -{\frac {\pi }{2}}

,

{\frac {\gamma -\alpha }{2}}\neq 0

,

\,\,\left({\frac {\gamma -\alpha }{2}}+\alpha -\beta +{\frac {\pi }{2}}\right)\neq 0

,

\gamma \neq \alpha

,

\,\,\alpha -\beta +{\frac {\pi }{2}}=0

;

2)

\gamma \neq \alpha

,

\,\,\alpha -\beta -{\frac {\pi }{2}}=0

,

откуда окончательно получаем^[26]:

\beta =\alpha \pm {\frac {\pi }{2}}

.

Отображения с полуплоскостью

1. Единичный круг. На комплексной плоскости $\mathbb {C} (z)$ единичный круг $|z|<1$ и верхняя полуплоскость $\operatorname {Im} z>0$ дробно-линейно изоморфны^[27], поскольку верхняя полуплоскость конформно отображается на единичный круг следующим дробно-линейным отображением^[2]^[3]^[4]:

e^{i\theta }{\frac {z-a}{z-{\bar {a}}}},\,a\in \mathbb {C} ,\,\theta \in \mathbb {R} ,\,\operatorname {Im} a>0.

2. Полуполоса. На комплексной плоскости $\mathbb {C}$ с координатами $z=x+iy$ однолистное и конформное преобразование $w=\sin z$ отображает полуполосу $-{\frac {\pi }{2}}<x<{\frac {\pi }{2}},\,y>0$ на верхнюю полуплоскость. На рисунке внизу показано соответствие линий при этом преобразовании, а именно^[28]:

вертикальные лучи $\{x=x_{0},\,0<y<\infty \}$ отображаются на верхнюю полуплоскость в части гипербол с фокусами $\pm 1$ ;
горизонтальные отрезки $\{-{\frac {\pi }{2}}<x<{\frac {\pi }{2}},\,y=y_{0}\}$ отображаются на верхнюю полуплоскость в части эллипсов с теми же фокусами $\pm 1$ .

Преобразование полуполосы в полуплоскость
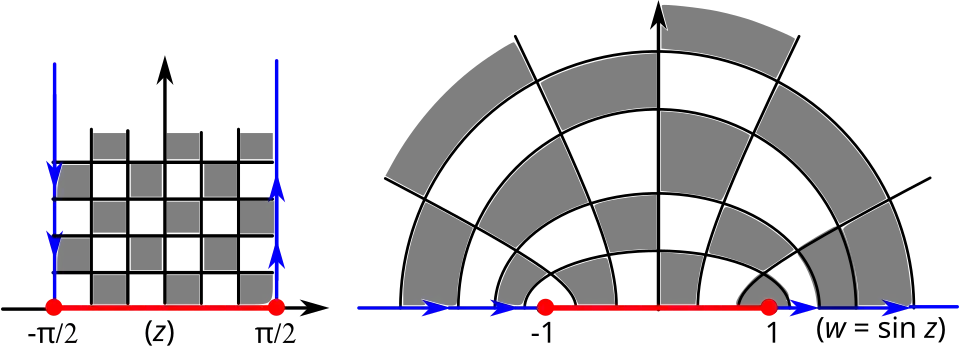$Преобразование вертикальной полуполосы в верхнюю полуплоскость функцией w = sin ⁡ z {\displaystyle w=\sin z}$
Преобразование вертикальной полуполосы в верхнюю полуплоскость функцией $w=\sin z$

Пересечение выпуклых фигур

Пересечение фигур $M_{1},\,M_{2},\,\dots ,\,M_{k}$ — фигура, которая состоит из всех тех точек, которые принадлежат сразу всем фигурам $M_{1},\,M_{2},\,\dots ,\,M_{k}$ ^[29].

Вполне возможно пересечение произвольного неограниченного количества фигур^[30].

Теорема 1. Пересечение произвольного количества выпуклых фигур суть снова выпуклая фигура, если оно включает хотя бы одну точку)^[30].

Доказательство^[30]

Рассмотрим пересечение $M$ бесконечного числа выпуклых фигур $M_{1},\,M_{2},\,\dots .$ Найдём две любые точки $A$ и $B$ новой фигуры $M$ . По определению пересечения, эти точки принадлежат любой из фигур $M_{1},\,M_{2},\,\dots .$ Поскольку эти фигуры $M_{1},\,M_{2},\,\dots$ выпуклы, то любая их них включает и весь отрезок $AB$ . Но тогда и пересечение этих фигур $M_{1},\,M_{2},\,\dots$ — фигура $M$ — включает этот отрезок $AB$ . Таким образом, фигура $M$ вместе с двумя любыми точками $A$ и $B$ включает также и соединяющий их отрезок $AB$ и по определению выпукла.

Следующую теорему можно взять за новое определение выпуклой фигуры^[16].

Теорема 2. Плоская фигуры выпукла тогда и только тогда, когда её можно представить как пересечение некоторого количества полуплоскостей^[16].

Замечание. Полуплоскостями, пересечение которых представляет собой заданную выпуклую фигуру $M$ , могут быть все полуплоскости, которые содержат эту фигуру $M$ и ограничены её опорными прямыми^[16].

Доказательство^[30]

1. Достаточность. Из теоремы 1 вытекает, что, поскольку плоскость выпукла, то пересечение произвольного количества полуплоскостей есть выпуклая фигура.

2. Необходимость. Существуют полуплоскости, которым целиком принадлежит фигура $M$ ; например, каждая опорная прямая фигуры $M$ разбивает плоскость на две полуплоскости, в одной из которых лежит $M$ . Далее, пересечение всех полуплоскостей, в которых лежит $M$ , — фигура $N$ выпукла и содержит $M$ .

Докажем, что $M$ и $N$ совпадают. Рассмотрим точку $A$ , не принадлежащую фигуре $M$ . Найдём какую-нибудь прямую $l$ , которая разделяет выпуклую фигуру $M$ и выпуклую ограниченную фигуру $A$ . Тогда полуплоскость, определяемая прямой $l$ и содержащая фигуру $M$ , точку $A$ не содержит, и по построению фигуры $N$ точка $A$ не лежит в $N$ . Следовательно, точки, не принадлежащие $M$ , не принадлежат и $N$ , то есть $M$ и $N$ совпадают.

Выпуклый многосторонник

Выпуклый многосторонник — фигура на плоскости, которую можно представить как пересечение конечного числа замкнутых полуплоскостей^[16].

Простейший выпуклый многосторонник — это односторонник, то есть замкнутая полуплоскость^[16].

Треугольник — простейший ограниченный выпуклый многосторонник; при $n\geqslant 3$ выпуклые трёхсторонники, четырёхсторонники и так далее бывают ограниченные и неограниченные. Отрезок — пример выпуклого ограниченного четырёхсторонника^[16].

Примечания

1 2 3 4 5 6 Перевод на англ. см. в закладке «Обсуждение» статьи
1 2 3 4 5 6 7 8 9 10 Полуплоскость. БСЭ 3, 1975.
1 2 3 4 5 6 7 8 9 10 Полуплоскость. МЭ, 1984.
1 2 3 4 5 6 7 8 9 10 Полуплоскость. МЭС, 1988.
1 2 3 4 Курант Р., Роббинс Г. Что такое математика?, 2015, Глава IV. Проективная геометрия… Приложение…, с. 254—255.
1 2 3 4 5 Рохлин В. А. Площадь и объём, 1966, 2.1. Внутренние, внешние и граничные точки, с. 13—14.
↑ Киселёв М. А. Элементарная геометрия, 1980, 275. Аксиомы плоскости, с. 172.
1 2 3 4 Гусятников П. Б. Векторная алгебра в примерах и задачах, 1985, Главка 1. Сведения из элементарной геометрии. § 1. Некоторые необходимые определения и обозначения, с. 7.
↑ Киселёв М. А. Элементарная геометрия, 1980, 304. Определения, с. 182.
↑ Понарин Я. П. Планиметрия, преобразования плоскости, 2004, 12.2. Следствия из общих формул площади четырехугольника, с. 91.
1 2 3 Alfred Gray. Modern Differential Geometry, 2006, 6.4 Convex Plane Curves, p. 164.
↑ Гусев В. А. Математика, 2013, 5. Плоскости, с. 388.
↑ Киселёв М. А. Элементарная геометрия, 1980.
↑ Рохлин В. А. Площадь и объём, 1966, 2.1. Внутренние, внешние и граничные точки, с. 16.
↑ Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 1.1. Определение. Примеры, с. 182.
1 2 3 4 5 6 7 Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.2. Выпуклые многосторонники и многогранники, с. 209.
↑ Alfred Gray. Modern Differential Geometry, 2006, 26.2 Examples of Abstract Metrics, p. 876.
↑ Пятецкий-Шапиро И. И. Геометрия классических областей и теория автоморфных функций, 1961, Введение, с. 9.
↑ Шабат Б. В. Введение в комплексный анализ. Т. 2, 1976, 2. Простейшие области, с. 19.
1 2 3 Розенфельд Б. А. Аксиомы и основные понятия геометрии, 1963, 6.3. Аксиомы порядка, с. 36.
↑ Jaap Korevaar, Jan Wiegerinck. Several complex variables, 2011, 2.1 General theory of analytic continuation, p. 26.
↑ John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 6.
↑ John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 6–7.
1 2 John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 7.
↑ John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 7—8.
1 2 John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 8.
↑ Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Т. 1, 2004, 3.7. Дробно-линейные изоморфизмы основных областей, с. 34.
↑ Шабат Б. В. Введение в комплексный анализ. Т. 1, 1976, 13. Показательная функция, с. 73—74.
↑ Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.1. Пересечение выпуклых фигур, с. 207.
1 2 3 4 Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.1. Пересечение выпуклых фигур, с. 208.

Источники

Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела // Энциклопедия элементарной математики (рус.) / гл. ред.: П. С. Александров, А. И. Маркушевич, А. Я. Хинчин; редакторы книги пятой: В. Г. Болтянский, И. М. Яглом. — М.: «Наука», 1966. — Т. 5 Геометрия. — С. 181—269. — 624 с., ил. — 25 000 экз.
Гусев В. А., Мордкович А. Г. Математика : учебно-справочное пособие (рус.). — М.: Издательство «Астрель», 2013. — 671,[1] с., ил. — (Справочник школьника). — Доп. тираж 2000 экз. — ISBN 978-5-271-07165-2.
Гусятников П. Б., Резниченко С. В.. Векторная алгебра в примерах и задачах: Учеб. пособие для студентов инж.-тех. спец. вузов (рус.). — М.: «Высшая школа», 1985. — 232 с., ил. — 50 000 тыс. экз.
Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу (рус.). — М.: МИАН, 2004. — Т. 1. — 175 с., ил. — 200 экз. — ISBN 5-98419-007-9 (ч. I). — ISBN 5-98419-006-0.
Киселёв М. А. Элементарная геометрия. Книга для учителя (рус.). — копия 12-е изд. (1931). — М.: «Просвещение», 1980. — 286 с., ил.
Курант Р., Роббинс Г. Что такое математика? Элементарный очерк идей и методов = Richard Courant, Herbert Robbins. What Is Mathematics? An Elementary Approach to Ideas and Methods (рус.) / пер. с англ. под ред. А. Н. Колмогорова. — 7-е изд., стереотип. — М.: Издательство МЦНМО, 2015. — 564 с., ил. — 2000 экз. — ISBN 978-5-4439-0628-7.
Понарин Я. П. Элементарная геометрия: В 2 т (рус.). Т. 1: Планиметрия, преобразования плоскости. — М.: Издательство МЦНМО, 2004. — 311 с., ил. — 2000 экз. — ISBN 5-94057-170-0. — ISBN 5-94057-171-9 (том 1).
Полуплоскость // Большая советская энциклопедия. (В 30 томах) (рус.) / гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская энциклопедия», 1975. — Т. 20 Плата — проб. — С. 259. — 608 с., ил., 17 л. ил., 4 л. карт. — 630 тыс. экз.
Полуплоскость // Математическая энциклопедия (рус.) / гл. ред. И. М. Виноградов. — М.: «Советская энциклопедия», 1984. — Т. 4 Ок—Сло. — Стб. 462. — 1216 стб., ил. — 148 900 экз.
Полуплоскость // Математический энциклопедический словарь (рус.) / гл. ред. Ю. В. Прохоров; ред. кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. — М.: «Советская энциклопедия», 1988. — С. 474. — 847 с., ил. — 148 900 экз.
Пятецкий-Шапиро И. И. Геометрия классических областей и теория автоморфных функций (рус.). — М.: Физматгиз, 1961. — 191 с. — (Современные проблемы математики). — 5000 экз.
Розенфельд Б. А. Аксиомы и основные понятия геометрии // Энциклопедия элементарной математики (рус.) / гл. ред.: П. С. Александров, А. И. Маркушевич, А. Я. Хинчин; редакторы книги четвёртой: В. Г. Болтянский, И. М. Яглом. — М.: Физматлит, 1963. — Т. 4 Геометрия. — С. 9—48. — 567 с., ил. — 20 000 экз.
Рохлин В. А. Площадь и объём // Энциклопедия элементарной математики (рус.) / гл. ред.: П. С. Александров, А. И. Маркушевич, А. Я. Хинчин; редакторы книги пятой: В. Г. Болтянский, И. М. Яглом. — М.: «Наука», 1966. — Т. 5 Геометрия. — С. 5—87. — 624 с., ил. — 25 000 экз.
Шабат Б. В. Введение в комплексный анализ (рус.). — 2-е изд, перераб. и доп. — М.: «Наука», 1976. — Т. 1. — 320 с., ил. — 20 000 экз.
Шабат Б. В. Введение в комплексный анализ (рус.). — 2-е изд, перераб. и доп. — М.: «Наука», 1976. — Т. 2. — 400 с., ил. — 20 000 экз.
John B. Conway. Functions of one complex variable (англ.) / Managing Editor P. R. Halmos; Editorial Board: F. W. Gehring, C. C. Moore. — Second Edition. — New York · Heidelberg · Berlin: Springer-Verlag, 1978. — XIV+319 p. — (Graduate texts in mathematics; 11).
Alfred Gray. Modern Differential Geometry of Curves and Surfaces with Mathematica® (англ.) / revised by Elsa Abbena and Simon Salamon. — Third Edition. — Boca Raton · London · New York · Oxford: Chapman & Hall/CRC, 2006. — XII+982 p. — (Studies in Advanced Mathematics). — ISBN 1-58488-448-7. — ISBN 978-1-58488-448-4.
Jaap Korevaar, Jan Wiegerinck. Several complex variables (англ.). — Amsterdam: University of Amsterdam, 2011. — V+260 p.

[англ-1] 1 2 3 4 5 6 Перевод на англ. см. в закладке «Обсуждение» статьи

[БСЭ-2] 1 2 3 4 5 6 7 8 9 10 Полуплоскость. БСЭ 3, 1975.

[МЭ-3] 1 2 3 4 5 6 7 8 9 10 Полуплоскость. МЭ, 1984.

[МЭС-4] 1 2 3 4 5 6 7 8 9 10 Полуплоскость. МЭС, 1988.

[Курант254-5-5] 1 2 3 4 Курант Р., Роббинс Г. Что такое математика?, 2015, Глава IV. Проективная геометрия… Приложение…, с. 254—255.

[Рохлин13-4-6] 1 2 3 4 5 Рохлин В. А. Площадь и объём, 1966, 2.1. Внутренние, внешние и граничные точки, с. 13—14.

[_edda512b07c1c03f-7] Киселёв М. А. Элементарная геометрия, 1980, 275. Аксиомы плоскости, с. 172.

[Гусятников7-8] 1 2 3 4 Гусятников П. Б. Векторная алгебра в примерах и задачах, 1985, Главка 1. Сведения из элементарной геометрии. § 1. Некоторые необходимые определения и обозначения, с. 7.

[_717a781f5aa1e5eb-9] Киселёв М. А. Элементарная геометрия, 1980, 304. Определения, с. 182.

[_ae97ab6c801b2a73-10] Понарин Я. П. Планиметрия, преобразования плоскости, 2004, 12.2. Следствия из общих формул площади четырехугольника, с. 91.

[Gray164-11] 1 2 3 Alfred Gray. Modern Differential Geometry, 2006, 6.4 Convex Plane Curves, p. 164.

[_774eff05db7a23b3-12] Гусев В. А. Математика, 2013, 5. Плоскости, с. 388.

[_4c59396cead27b0c-13] Киселёв М. А. Элементарная геометрия, 1980.

[Рохлин16-14] Рохлин В. А. Площадь и объём, 1966, 2.1. Внутренние, внешние и граничные точки, с. 16.

[_899d66f3241fe288-15] Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 1.1. Определение. Примеры, с. 182.

[Болтянский209-16] 1 2 3 4 5 6 7 Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.2. Выпуклые многосторонники и многогранники, с. 209.

[_03273b42b85a8b29-17] Alfred Gray. Modern Differential Geometry, 2006, 26.2 Examples of Abstract Metrics, p. 876.

[_0427234d98ca3762-18] Пятецкий-Шапиро И. И. Геометрия классических областей и теория автоморфных функций, 1961, Введение, с. 9.

[_d81deffebc30f3d7-19] Шабат Б. В. Введение в комплексный анализ. Т. 2, 1976, 2. Простейшие области, с. 19.

[Розенфельд36-20] 1 2 3 Розенфельд Б. А. Аксиомы и основные понятия геометрии, 1963, 6.3. Аксиомы порядка, с. 36.

[_a37eeec2c70e0a71-21] Jaap Korevaar, Jan Wiegerinck. Several complex variables, 2011, 2.1 General theory of analytic continuation, p. 26.

[_797cc9ca85030eaa-22] John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 6.

[_e47fe03f9e722cca-23] John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 6–7.

[_797cc9ca85030eab-24] 1 2 John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 7.

[_ff43194a7f28e7f5-25] John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 7—8.

[_797cc9ca85030ea4-26] 1 2 John B. Conway. Functions of one complex variable, 1978, I. The Complex Number System, §5. Lines and half planes in the complex plane, p. 8.

[_63491f6ae616baac-27] Домрин А. В., Сергеев А. Г. Лекции по комплексному анализу. Т. 1, 2004, 3.7. Дробно-линейные изоморфизмы основных областей, с. 34.

[_18022146548926c3-28] Шабат Б. В. Введение в комплексный анализ. Т. 1, 1976, 13. Показательная функция, с. 73—74.

[_1725efc526ef5adb-29] Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.1. Пересечение выпуклых фигур, с. 207.

[Болтянский208-30] 1 2 3 4 Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела, 1966, 3.1. Пересечение выпуклых фигур, с. 208.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]