Выпуклый многосторонник

Вы́пуклый многосторо́нник^{[комм 1]} — фигура на плоскости, которую можно представить как пересечение конечного числа замкнутых полуплоскостей^[1].

Простейший выпуклый многосторонник — это односторонник, то есть замкнутая полуплоскость^[1].

Треугольник — простейший ограниченный выпуклый многосторонник; при ${\displaystyle n\geqslant 3}$ выпуклые трёхсторонники, четырёхсторонники^{[комм 1]} и так далее бывают ограниченные и неограниченные. Отрезок — пример выпуклого ограниченного четырёхсторонника^[1].

Выпуклый многоугольник — то же самое, что и ограниченный выпуклый многосторонник^[2].

Выпуклый многогранник — обобщение на трёхмерное пространство выпуклого многосторонника^[3].

Рассмотрим выпуклый многосторонник^{[комм 1]} ${\displaystyle M}$, который образован пересечением следующего множества ${\displaystyle n}$ замкнутых полуплоскостей^[1]:

${\displaystyle S=\{H_{1},\,H_{2},\,\dots ,\,H_{n}\}}$.

Лишняя полуплоскость — полуплоскость из множества замкнутых полуплоскостей ${\displaystyle S}$, образовывающих выпуклый многосторонник ${\displaystyle M}$, которая содержит пересечение всех остальных плоскостей из ${\displaystyle S}$^[1].

Лишнюю полуплоскость можно удалить из множества замкнутых полуплоскостей ${\displaystyle S}$, определяющих многосторонник ${\displaystyle M}$, при этом ${\displaystyle M}$ не изменится и будет определён меньшим числом полуплоскостей^[1].

Выпуклый ${\displaystyle n}$-сторонник — выпуклый многосторонник, образованный пересечением ${\displaystyle n}$ замкнутых полуплоскостей, среди которых нет лишних^[1][4].

Простейший выпуклый многосторонник — это односторонник, то есть просто замкнутая полуплоскость^[1].

Выпуклые двусторонники — это углы, меньшие ${\displaystyle 180^{\circ }}$, и полосы, а также прямые, которые представляются как пересечение двух замкнутых полуплоскостей. Выпуклые односторонники и двусторонники всегда не ограничены^[1].

• Выпуклые двусторонники
• 
  Угол меньше ${\displaystyle 180^{\circ }}$
• 
  Полоса
• 
  Прямая

Треугольник — простейший ограниченный выпуклый многосторонник; при ${\displaystyle n\geqslant 3}$ выпуклые трёхсторонники, четырёхсторонники^{[комм 1]} и так далее бывают ограниченные и неограниченные. Отрезок — пример выпуклого ограниченного четырёхсторонника^[1].

• Выпуклые трёхсторонники
• 
  Луч
• 
  Точка
• 
  Угол без треугольника
• 
  Полуполоса
• 
  Треугольник

• Выпуклые четырёхсторонники
• 
  Точка
• 
  Отрезок
• 
  Ограниченный четырёхсторонник
• 
  Неограниченный четырёхсторонник

Произвольная выпуклая фигура, расположенная на прямой (точка, отрезок, луч или вся прямая), есть выпуклый многосторонник^[5].

Нульмерный выпуклый многосторонник — это точка. Одномерные выпуклые многосторонники — отрезок, луч и прямая. Двумерные выпуклые многосторонники — все остальные выпуклые многосторонники^[5].

• Одномерные выпуклые многосторонники
• 
  Отрезок как выпуклый четырёхсторонник
• 
  Луч как выпуклый трёхсторонник
• 
  Прямая как выпуклый двусторонник

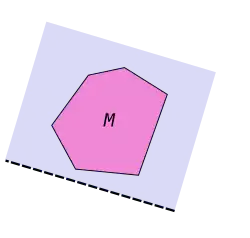
Рассмотрим некоторый выпуклый ${\displaystyle n}$-сторонник ${\displaystyle M}$ и ${\displaystyle n}$ полуплоскостей ${\displaystyle H_{1},\,H_{2},\,\dots ,\,H_{k}}$, пересечение которых определяет ${\displaystyle M}$. Обозначим через ${\displaystyle l_{1},\,l_{2},\,\dots ,\,l_{k}}$ граничные прямые соответственно полуплоскостей ${\displaystyle H_{1},\,H_{2},\,\dots ,\,H_{k}}$^[5].

Предложение 1. Каждая из описанных прямых ${\displaystyle l_{1},\,l_{2},\,\dots ,\,l_{k}}$ представляет собой опорную прямую данной фигуры ${\displaystyle M}$^[5].

Доказательство. Поскольку, по условию, фигура ${\displaystyle M}$ полностью принадлежит полуплоскости ${\displaystyle H_{i}}$, ${\displaystyle i=1,\,2,\,\dots ,\,k}$, то она находится по по дну сторону от прямой ${\displaystyle l_{i}}$. Предположим, что прямая ${\displaystyle l_{i}}$ совсем не имеет общих точек с фигурой ${\displaystyle M}$, получим, что полуплоскость ${\displaystyle H_{i}}$ лишняя, что противоречит тому условию, что ${\displaystyle M}$ — выпуклый ${\displaystyle n}$-сторонник и среди плоскостей ${\displaystyle H_{1},\,H_{2},\,\dots ,\,H_{k}}$ нет лишних^[5]. □

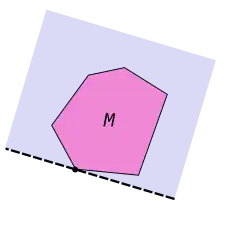
Рассмотрим свойства двумерного выпуклого многосторонника ${\displaystyle M}$^[5].

Предложение 1. Каждая прямая ${\displaystyle l_{i}}$ из опорных прямых ${\displaystyle l_{1},\,l_{2},\,\dots ,\,l_{k}}$ пересекается с границей двумерного выпуклого многосторонника ${\displaystyle M}$ либо по отрезку, либо по лучу, либо целиком лежит на границе ${\displaystyle M}$^[5].

Доказательство. Поскольку, по условию, фигура ${\displaystyle M}$ полностью принадлежит полуплоскости ${\displaystyle H_{i}}$, ${\displaystyle i=1,\,2,\,\dots ,\,k}$, то она находится по по дну сторону от прямой ${\displaystyle l_{i}}$. Предположим, что прямая ${\displaystyle l_{i}}$ имеет только одну общую граничную точку с границей фигуры ${\displaystyle M}$, получим, что полуплоскость ${\displaystyle H_{i}}$ лишняя, что противоречит тому условию, что ${\displaystyle M}$ — выпуклый ${\displaystyle n}$-сторонник и среди плоскостей ${\displaystyle H_{1},\,H_{2},\,\dots ,\,H_{k}}$ нет лишних^[5]. □

• Множества пересечений опорной прямой и границы фигуры
• 
  Отрезок
• 
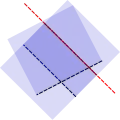  Луч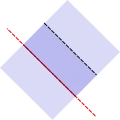
• 
  Прямая

Сторона выпуклого многосторонника — часть опорной прямой выпуклого многосторонника, принадлежащей его границе^[3].

У выпуклого ${\displaystyle n}$-сторонника ${\displaystyle n}$ сторон^[3].

Вершина выпуклого многосторонника — конец стороны выпуклого многосторонника^[3].

Альтернативное определение: сторона выпуклого многосторонника — вся опорная прямая выпуклого многосторонника^[3][6].

Рассмотрим двумерный выпуклый ${\displaystyle n}$-сторонник ${\displaystyle M}$ при ${\displaystyle n\geqslant 2}$. Граница такого многосторонника ${\displaystyle M}$ есть ${\displaystyle n}$-звенная ломаная. Если многосторонник ${\displaystyle M}$ ограничен, то эта ломаная замкнута, если не ограничен, то эта ломаная включает два луча. В первом случае у многосторонника ${\displaystyle M}$ ${\displaystyle n}$ вершин, во втором — ${\displaystyle n-1}$^[3].

• Болтянский В. Г., Яглом И. М. Выпуклые фигуры и тела // Энциклопедия элементарной математики (рус.) / гл. ред.: П. С. Александров, А. И. Маркушевич, А. Я. Хинчин; редакторы книги пятой: В. Г. Болтянский, И. М. Яглом. — М.: «Наука», 1966. — Т. 5 Геометрия. — С. 181—269. — 624 с., ил. — 25 000 экз.
• Сидоров Л. А. Многоугольник // Математическая энциклопедия (рус.) / гл. ред. И. М. Виноградов. — М.: «Советская энциклопедия», 1982. — Т. 3 Коо—Од. — Стб. 749—752. — 1184 стб., ил. — 150 000 экз.
• Яглом И. М. Комплексные числа и их применение в геометрии (рус.). — М.: Физматгиз, 1963. — 192 с., ил. — 43 000 экз.