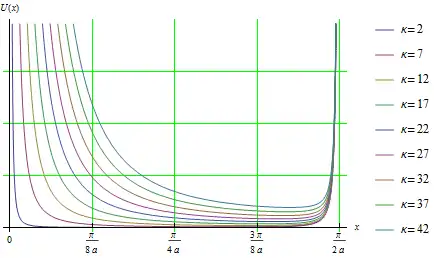
Уравнение Шрёдингера с потенциалом Пёшль — Теллера
Стационарное уравнение Шрёдингера с потенциалом Пёшль — Теллера имеет вид:

Если ввести обозначение  , то оно примет вид:
, то оно примет вид:

После замены переменных

получим

Так как точки 0 и 1 являются особыми, то естественно представить решение в виде:

Если выбрать

то уравнение приведётся к гипергеометрическому виду:

Общее решение данного уравнения может быть выражено через гипергеометрические функции:

где введены обозначения:

Если учесть граничные условия:

то получим собственные функции

где константа вычисляется с учётом нормировки:

Соответствующие уровни энергии равны:

Примечания
- ↑ G. Pöschl, E. Teller. Bemerkungen zur Quantenmechanik des anharmonischen Oszillators (нем.) // Zeitschrift für Physik. — 1933. — Bd. 83, Nr. 3-4. — S. 143–151. — doi:10.1007/BF01331132.
Литература
- З. Флюгге. Задачи по квантовой механике. — Издательство ЛКИ, 2008. — Т. 1.
|
|---|
| Одномерные без учёта спина | |
|---|
| Многомерные без учёта спина | |
|---|
| С учётом спина | |
|---|