Знак равенства
| Знак равенства | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = | ||||||||||||
|
Изображение
|
||||||||||||
|
||||||||||||
| Характеристики | ||||||||||||
| Название | equals sign | |||||||||||
| Юникод | U+003D | |||||||||||
| HTML-код |
= или = |
|||||||||||
| UTF-16 | 0x3D | |||||||||||
| URL-код | %3D | |||||||||||

Знак ра́венства (=) в математике — символ, который пишется между двумя идентичными по своему значению математическими выражениями. Оба эти выражения чаще всего числовые, но могут быть и любыми другими, для которых определено понятие равенства — например, допускаются равенства векторные, логические, текстовые, матричные, тензорные, аналитические, теоретико-множественные и другие.
История появления
Знак равенства в современной форме предложил валлийский математик XVI века Роберт Рекорд в своём труде The Whetstone of Witte («Оселок остроумия», 1557)[1]. Он обосновал применение двух параллельных штрихов так (орфография оригинала — ранненовоанглийский):
| And to auoide the tediouſe repetition of theſe woordes : is equalle to : I will ſette as I doe often in woorke vſe, a paire of paralleles, or Gemowe lines of one lengthe, thus: =, bicauſe noe .2. thynges, can be moare equalle. | И чтобы избежать утомительного повторения этих слов : является равным : я буду рисовать, как часто делаю в рабочем обиходе, пару параллелей, или линий-близнецов одной длины, таким образом: =, ибо никакие две вещи не могут быть более равными. | |||
The Whetstone of Witte[2] | ||||
До этого в античной и средневековой математике равенство обозначалось словесно (например est egale). Как можно видеть на изображении страницы из книги Рекорда, введённый им знак равенства был значительно длиннее современного. В своих более ранних трудах в качестве символа равенства Рекорд использовал букву Z[1].

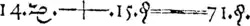
Символ Рекорда получил распространение далеко не сразу. Рене Декарт в XVII веке для обозначения равенства использовал символ æ (от лат. aequalis), а современный знак равенства у него означал, что последующее выражение может быть отрицательным. Франсуа Виет знаком равенства обозначал операцию вычитания. В континентальной Европе знак «=» был введён Лейбницем только на рубеже XVII—XVIII веков, то есть более чем через 100 лет после смерти Роберта Рекорда.
Таблица математических знаков (символов) эквивалентности с кодами Unicode
| знак | Unicode значение | Название знака | знак | Unicode значение | Название знака | |
|---|---|---|---|---|---|---|
| = | U+003D | равно | ≠ | U+2260 | не равно | |
| ≃ | U+2243 | асимптотически равно | ≄ | U+2244 | асимптотически не равно | |
| ≅ | U+2245 | конгруэнтность (геометрическое равенство) | ≆ | U+2246 | равно приблизительно, но не точно | |
| ≇ | U+2247 | не равен ни приблизительно, ни точно | ||||
| ≌ | U+224C | конгруэнтность | ≂ | U+2242 | ||
| ≈ | U+2248 | примерно равно | ≉ | U+2249 | ||
| ∝ | U+221D | пропорционально | | |||
| ≡ | U+2261 | идентично, тождество | ≢ | U+2262 | не идентично | |
| ≊ | U+224A | равно или почти равно | ≋ | U+224B | тройная тильда, конгруэнтность | |
| ≍ | U+224D | эквивалентно | ≣ | U+2263 | строго эквивалентно | |
| ≎ | U+224E | геометрически эквивалентно | ≏ | U+224F | геометрически неэквивалентно | |
| ≐ | U+2250 | округлённо равно | ≑ | U+2251 | ||
| ≒ | U+2252 | обратное преобразование Лапласа | ≓ | U+2253 | прямое преобразование Лапласа | |
| ≔ | U+2254 | присваивание | ≕ | U+2255 | ||
| ≘ | U+2258 | соответствует | ≚ | U+225A | равноугольный | |
| ≗ | U+2257 | ≙ | U+2259 | соответствует | ||
| ≞ | U+225E | ≟ | U+225F | может быть равно | ||
| ≜ | U+225C | Равно по определению | ≝ | U+225D | Равно по определению | |
| ≛ | U+225B | ≖ | U+2256 |
Похожие символы
- «≠» — не равно (в программировании обычно используется «!=», «<>» или «#»).
- «≈» — «приблизительно равно». Используется при обозначении двух величин, разницей между которыми в данной задаче можно пренебречь.
- «≃» — используется для обозначения гомеоморфных пространств в топологии.
- «~» — «асимптотически равно», «пропорционально». Иногда используется для обозначения пропорциональности двух величин или подобия в геометрии.
- «≡» — «тождественно равно». Используется для обозначения двух идентичных (равных при любых значениях входящих параметров) выражений. Также для сравнения по модулю.
- «:=» — часто используется для обозначения оператора присваивания, а также, наряду с «≜» и «≝» для равенства по определению.
- «≌» — используется для обозначения конгруэнтных фигур в геометрии и диффеоморфных многообразий в дифференциальной геометрии.
- «≅» — используется при отсутствии полного лексического или стилистического соответствия иноязычного слова или выражения и его русского переводного эквивалента[3].
Применение в информатике
В языках программирования символ = чаще всего используется для операций сравнения и/или присваивания. В некоторых языках (например, Basic) символ используется для обеих операций, в зависимости от контекста. В языках C, PHP и т. п. = обозначает присваивание, равенство записывается как ==. В Pascal, напротив, = обозначает равенство, присваивание обозначается :=. В Perl операторы для сравнения строк отличаются от операторов для сравнения чисел, равенство строк проверяет eq.
Примечания
- 1 2 Токарева Т. А. Из ранней истории алгебры в Англии Архивная копия от 26 ноября 2020 на Wayback Machine // Институт истории естествознания и техники им. С. И. Вавилова. Годичная научная конференция, 1995. М.: «Янус-К», 1996. С. 129—131.
- ↑ Robert Recorde. The whetstone of witte, whiche is the seconde parte of Arithmetike: containyng thextraction of Rootes: The Coßike practise, with the rule of Equation: and the woorkes of Surde Nombers (англ.). — London: John Kyngstone, 1557. — P. 238.
- ↑ Апресян, 1993, с. 25.
Источники
- Новый большой англо-русский словарь : в 3 т. / Апресян Ю. Д., Медникова Э. М., Петрова А. В. и др. Под общ. рук. Ю. Д. Апресяна. — 1-е изд. — М. : Русский язык, 1993. — Т. I : A—F. — 832 с. — ISBN 5-200-01954-0.
Литература
Ссылки
- = на сайте Scriptsource.org (англ.)
