Термодинамическая бета

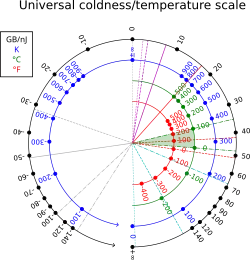
В статистической термодинамике термодинамическая бета, также известная как холодность,^[1] является величиной, обратной термодинамической температуре системы:$${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}}$$ (где T — температура, а k_B — постоянная Больцмана).^[2]

Термодинамическая бета имеет размерность, обратную энергии (в единицах СИ, обратный джоуль, ${\displaystyle [\beta ]={\textrm {J}}^{-1}}$). В нетепловых единицах её также можно измерять в байтах на джоуль или, что удобнее, в гигабайтах на наноджоуль;^[3] 1 K⁻¹ эквивалентен примерно 13 062 гигабайтам на наноджоуль; при комнатной температуре: T = 300 K, β ≈ 44 ГБ/нДж ≈ 39 эВ⁻¹ ≈ 2,4⋅10²⁰ Дж⁻¹. Коэффициент преобразования: 1 ГБ/нДж = ${\displaystyle 8\ln 2\times 10^{18}}$ Дж⁻¹.

Термодинамическая бета, по сути, является связующим звеном между теорией информации и статистической механикой в интерпретации физической системы через её энтропию и термодинамикой, связанной с её энергией. Она выражает реакцию энтропии на увеличение энергии. Если к системе добавляется небольшое количество энергии, то β описывает степень рандомизации системы.

Через статистическое определение температуры как функции энтропии, функцию холодности можно вычислить в микроканоническом ансамбле по формуле

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}\,={\frac {1}{k_{\rm {B}}}}\left({\frac {\partial S}{\partial E}}\right)_{V,N}}$

(т. е. частная производная энтропии S по энергии E при постоянном объёме V и числе частиц N).

С точки зрения статистики, β — это числовая величина, связывающая две макроскопические системы в равновесии. Точная формулировка следующая. Рассмотрим две системы, 1 и 2, находящиеся в тепловом контакте, с соответствующими энергиями E₁ и E₂. Предположим, что E₁ + E₂ = некоторая постоянная E. Количество микросостояний каждой системы обозначим Ω₁ и Ω₂. В рамках наших предположений Ω_i зависит только от E_i. Мы также предполагаем, что любое микросостояние системы 1, совместимое с E₁, может сосуществовать с любым микросостоянием системы 2, совместимым с E₂. Таким образом, количество микросостояний для объединённой системы равно

${\displaystyle \Omega =\Omega _{1}(E_{1})\Omega _{2}(E_{2})=\Omega _{1}(E_{1})\Omega _{2}(E-E_{1}).\,}$

Мы выведем β из основного постулата статистической механики:

Когда объединённая система достигает равновесия, число Ω максимизируется.

(Другими словами, система естественным образом стремится к максимальному числу микросостояний.) Следовательно, в равновесии:

${\displaystyle {\frac {d}{dE_{1}}}\Omega =\Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})+\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})\cdot {\frac {dE_{2}}{dE_{1}}}=0.}$

Но E₁ + E₂ = E подразумевает

${\displaystyle {\frac {dE_{2}}{dE_{1}}}=-1.}$

Так что

${\displaystyle \Omega _{2}(E_{2}){\frac {d}{dE_{1}}}\Omega _{1}(E_{1})-\Omega _{1}(E_{1}){\frac {d}{dE_{2}}}\Omega _{2}(E_{2})=0}$

т. е.

${\displaystyle {\frac {d}{dE_{1}}}\ln \Omega _{1}={\frac {d}{dE_{2}}}\ln \Omega _{2}\quad {\mbox{в равновесии.}}}$

Вышеприведённое соотношение мотивирует определение β:

${\displaystyle \beta ={\frac {d\ln \Omega }{dE}}.}$

Когда две системы находятся в равновесии, они имеют одинаковую термодинамическую температуру T. Поэтому интуитивно можно ожидать, что β (определённая через микросостояния) каким-то образом связана с T. Эта связь обеспечивается основным постулатом Больцмана, записанным как

${\displaystyle S=k_{\rm {B}}\ln \Omega ,}$

где k_B — постоянная Больцмана, S — классическая термодинамическая энтропия, а Ω — число микросостояний. Таким образом,

${\displaystyle d\ln \Omega ={\frac {1}{k_{\rm {B}}}}dS.}$

Подставляя в определение β из статистического определения выше, получаем

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}}}{\frac {dS}{dE}}.}$

Сравнивая с термодинамической формулой

${\displaystyle {\frac {dS}{dE}}={\frac {1}{T}},}$

имеем

${\displaystyle \beta ={\frac {1}{k_{\rm {B}}T}}={\frac {1}{\tau }}}$

где ${\displaystyle \tau }$ называется фундаментальной температурой системы и имеет размерность энергии.

Термодинамическая бета была первоначально введена в 1971 году (как Kältefunktion «функция холодности») Инго Мюллером, одним из сторонников школы мысли рациональной термодинамики,^[5][6] на основе более ранних предложений о функции «обратной температуры».^[1][7]

Распределение Больцмана

Канонический ансамбль

Модель Изинга