Условная дизъюнкция

Условная дизъюнкция
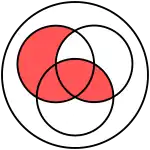Диаграмма Венна
Определение	${\displaystyle (q\rightarrow p)\land (\neg q\rightarrow r)}$
Таблица истинности	${\displaystyle (01000111)}$
Нормальные формы
Дизъюнктивная	${\displaystyle {\overline {p}}{\overline {q}}r+p{\overline {q}}r+pq{\overline {r}}+pqr}$
Конъюнктивная	${\displaystyle ({\overline {q}}+p)(q+r)}$
Полином Жегалкина	${\displaystyle pq\oplus qr\oplus r}$
Принадлежность предполным классам
Сохраняет 0	Да
Сохраняет 1	Да
Монотонна	Нет
Линейна	Нет
Самодвойственна	Нет

Условная дизъюнкция — тернарная (имеющая 3 операнда) логическая операция, введенная Алонзо Чёрчем^[1]. Результат условной дизъюнкции аналогичен результату более общей тернарной условной операции (if q then p else r), которая в том или ином виде используется в большинстве языков программирования как один из способов реализации ветвления в алгоритмах. Для операндов p, q и r, которые определяют истинность суждения, значение условной дизъюнкции [p, q, r] определяется по формуле

${\displaystyle [p,q,r]\leftrightarrow (q\to p)\land (\neg q\to r).}$

Другими словами, запись [p, q, r] эквивалентна записи: «Если q, то p, иначе r», которую можно переписать как «p или r, в зависимости от q или не q». Таким образом, для любых значений p, q и r значение [p, q, r] равно p, если q истинно, и равно r в противном случае.

В сочетании с константами, обозначающими каждое истинное значение, условная дизъюнкция является функционально полной для классической логики.^[2] Её таблица истинности выглядит следующим образом:

Условная дизъюнкция

${\displaystyle a}$	${\displaystyle b}$	${\displaystyle c}$	${\displaystyle [a,b,c]}$
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

Помимо условной дизъюнкции существуют и другие функционально полные тернарные операции.