Элемент длины
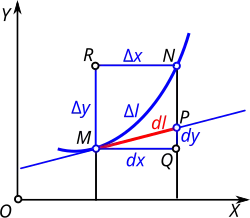
Элеме́нт длины́[1] (англ. line element; length element) — понятие математического анализа и дифференциальной геометрии, точнее — интегрального исчисления, элемент интегрирования, главная линейная часть приращения длины кривой, то есть малый отрезок касательной к кривой в рассматриваемой точке. Синонимы: дифференциал длины дуги[2], дифференциал дуги[2][3], элемент дуги[2], линейный элемент[4].
Обозначается или[2] . При вычислении циркуляции векторного поля представляется в векторной форме как
- ,
где — единичный вектор вдоль касательной[5][6][7][8].
Математическая запись элемента длины зависит от типа системы координат и вида рассматриваемой кривой. В случае декартовой системы элемент длины плоской кривой может выражаться формулой[2][3][9][10][11]
- .
Её правомерность видна из геометрических рассуждений. Пусть аргумент есть абсцисса . Элемент длины отвечает длине части касательной к дуге от точки касания до пересечения с приращённой ординатой (см. рис.)[2]. Дифференциал равен , дифференциал , и по теореме Пифагора для получается выписанное выражение[2]. По сути, формула приравнивает приращение касательной к дуге к главной части приращения длины дуги [9].
Квадрат элемента длины, выраженный через координаты пространства, называется метрической формой пространства[4].
Длина плоской или пространственной дуги в любом пространстве находится как криволинейный интеграл первого рода[4][12]:
- .
Элемент длины используется при вычислении криволинейных интегралов. Определённым интегралом с интегральным элементом длины можно выразить целый ряд геометрических и физических величин, например, длину кривой (с подынтегральной функцией 1), площадь или объём (со скалярной подынтегральной функцией), циркуляцию физического вектора по некоему контуру (с векторной подынтегральной функцией)[6][13].
Аналоги элемента длины больших размерностей — элемент площади и элемент объёма, которые принципиально отличаются от элемента длины тем, что не являются приращениями соответствующих величин — площади и объёма[14].
Элемент длины в декартовых координатах
Двумерный (плоский) случай
Рассмотрим на плоскости параметрически заданную кривую , определяемую в декартовой системе координат параметрическими уравнениями
причём у функций и производные непрерывны на отрезке . В силу формулы вычисления длины отрезка кривой длина переменной дуги задаётся следующей формулой[3]:
В этой формуле подынтегральная функция непрерывна, следовательно,
по свойству интеграла с верхним переменным пределом. Обе части этого равенства возведём в квадрат и потом умножим на , получим:
откуда по причине того, что
окончательно получаем квадрат элемента длины[3]:
Если в качестве параметра уравнений кривой взять длину переменной дуги (естественная параметризация), то есть положить
то тогда имеет место следующее равенство[3]:
Общий трёхмерный случай
Обобщая полученные результаты на трёхмерное пространство, получаем, что для параметрически заданной пространственной кривой , определяемой в декартовой системе координат параметрическими уравнениями
причём у функций , и производные непрерывны на отрезке , верна следующая формула для квадрата элемента длины[11][15][16]:
Из этой формулы следует, что если в качестве параметра уравнений пространственной кривой взять длину переменной дуги, то есть положить
то тогда имеет место следующее равенство[16][17]:
Элемент длины в криволинейных координатах
Плоский случай, полярные координаты
Элемент длины в полярной системе координат определяется следующей формулой[18]:
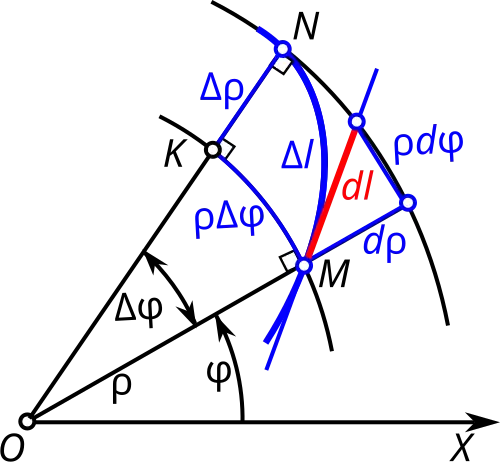
Вычислим элемент длины на плоскости в полярной системе координат. Пусть даны некоторая дуга и произвольная точка на ней (см. рис.). Проведём координатную окружность (с центром в начале координат ) радиуса . Рассмотрим криволинейный треугольник , образованный дугой окружности , отрезком и частью исходной дуги, причём у этого треугольника угол при вершине прямой. Теорема Пифагора для такого криволинейного треугольника в точности не соблюдается, но когда дуга бесконечно мала, сумма квадратов «катетов» эквивалентна квадрату «гипотенузы»:
- ,
то есть в других обозначениях
- ,
а эта формула и представляет элемент длины дуги в полярной системе координат[18].
Дифференциал дуги в полярной системе координат можно вычислить, исходя из элемента длины в декартовой системе координат
- ,
используя формулы, выражающие декартовы координаты через полярные[19]:
Действительно, вычислим дифференциалы координат
- ,
и подставим эти равенства в элемент длины в декартовых координатах, получим[19]:
-
- .
Цилиндрическая и сферическая системы
Запись трёхмерного элемента длины в цилиндрических и сферических координатах представлена в таблице. Цилиндрическая запись при и сферическая при превращаются в выражение для случая полярной системы[20][21][22][23].
| Система координат | Переменные | Квадрат элемента длины | Коэффициенты Ламе |
|---|---|---|---|
| Декартова | |||
| Цилиндрическая | |||
| Сферическая |
Некоторые несложные примеры расчёта
Для кривой имеем
- ,
- .
Ещё пример: для исходящего из начала координат луча ( const, const) будет
- ,
- .
И ещё: элемент длины арки циклоиды
равен[24]:
Элемент длины в римановых пространствах
В этом разделе представлены квадраты элемента длины, то есть метрические формы, в некоторых важнейших римановых пространствах[4].
Евклидово -мерное пространство[4]:
- .
- ,
где — постоянная, которая называется кривизной пространства Лобачевского; [26].
Трёхмерное пространство Лобачевского[4]:
- .
- ,
где ― скорость света, ― время события. В пространстве Минковского элемент длины может принимать мнимое значение[4].
- ,
где — произвольная положительно однородная функция относительно аргументов .
Элемент длины в произвольных координатах
Для элемента длины выведем формулу в произвольных координатах, опираясь на формулу в декартовых[28] и ради краткости ограничиваясь двумерной ситуацией (хотя рассуждения можно распространить на трёхмерную).
Пусть задана система координат , определяемая уравнениями
позволяющими по координатам и любой точки вычислить её декартовы координаты и . Примем[28], что функции и непрерывно дифференцируемы и обратимы, а якобиан этих функций не равен нулю: .
Пусть, далее, дана некоторая кривая и пусть — изменение параметра , а — элемент длины этой кривой, соответствующий . Тогда, подставив в уравнение
величины
- ,
где , , получим[29]:
- ,
где , , .
, и суть величины, которые при выбранных координатах полностью задаются выписанными выше уравнениями в любой точке плоскости, причём независимо от выбора кривой, проходящей через эту точку. Напротив, оба дифференциала и определяются только перемещением точки с координатами и .
Другими словами, выражение для есть квадратичная форма (метрическая форма) с аргументами , и коэффициентами , , [30]. Полученная формула выражает длину на евклидовой плоскости в произвольных координатах и как частный случай содержит прежнюю формулу для длины в декартовых[30].
Элемент длины в приложениях
Подынтегральная функция 1
Помимо чисто геометрических задач, понятие скалярного «элемента длины» широко применяется в физике при расчёте длины траектории частицы. Скажем, если траектория задана зависимостью радиус-вектора от времени , то (и так же для других компонент) и
- ,
где точка над символом означает производную по времени.
Элемент поверхности вращения
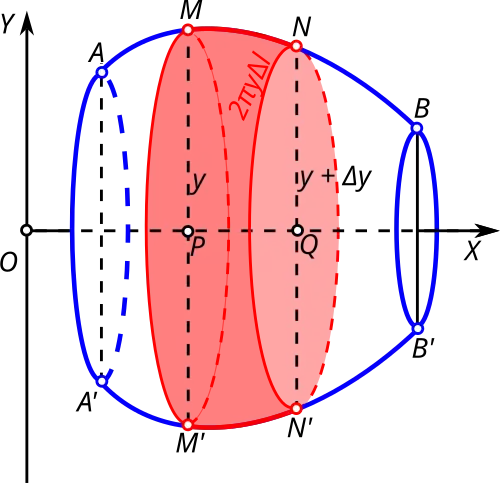
Пусть плоская дуга вращается вокруг оси . Тогда в трёхмерном пространстве получается поверхность вращения, площадь которой равна следующему выражению (см. рис.):
- ,
где — ордината меридиана , — элемент длины дуги меридиана, — элемент поверхности вращения, и — крайние значения параметра , через которые выражены координаты , [31][32][33].
Вычислим площадь поверхности вращения. Разделим поверхность вращения на параллельные кольца, а каждое кольцо заменим на боковую поверхность усечённого конуса, сохранив основания. Так как площади поверхностей этих усечённых конусов эквивалентны, то площадь кольца
- ,
а поскольку
- ,
то
- ,
откуда и следует доказываемая формула[31]:
- .
Пример. Найдём площадь поверхности, которая получается при вращении арки циклоиды
вокруг её основания. Сразу получаем[34]:
Сравним полученный результат с площадью осевого сечения, то есть с двойной площадью арки циклоиды , получим, что площадь поверхности вращения превышает площадь сечения в раза[35].
Пример. Найдём площадь поверхности, которая получается при вращении куска параболы
вокруг оси . Сразу получаем[36]:
Пример. Найдём площадь сферы радиуса . Эту сферу можно задать вращением полуокружности
вокруг оси абсцисс. Но такое явное задание окружности не непрерывно дифференцируемо, поскольку производная бесконечна при . Поэтому для удобства зададим окружность параметрически[37]:
Тогда получаем[37]:
Пример. Найдём площадь катеноида, то есть поверхности, которая получается при вращении дуги цепной линии
вокруг оси абсцисс. Сразу получаем[37]:
Работа силы
Рассмотрим движение материальной точки по непрерывно дифференцируемой кривой , где — переменная длина дуги, , причём на точку в положении действует сила , направленная по касательной к траектории материальной точки в направлении движения и имеющая модуль . Тогда работа силы вдоль кривой выражается следующей формулой[38]:
- .
В случае, когда положение материальной точки на траектории её движения задаётся на основе другого параметра (например, времени), причём длина пройденного пути
непрерывно дифференцируема, то получаем следующую формулу[39]:
- .
Статические моменты и центр тяжести кривой
Определения
Статические моменты точки относительно осей и — произведения и соответственно, где — масса материальной точки , имеющей координаты и на плоскости[40].
Рассмотрим спрямляемую кривую , где — переменная длина дуги. Кривая имеет массу, причём масса её дуги прямо пропорциональна длине дуги, то есть масса дуги длиной равна , где — некоторая постоянная[40].
Линейная плотность кривой — коэффициент пропорциональности , где дуга длиной имеет массу , то есть плотность кривой есть массе длины её дуги, которая приходится на единицу длины этой дуги[40].
Однородная кривая — кривая с линейной плотностью[40].
Пусть для простоты в дальнейшем , то есть дуга длиной имеет массу , в частности, масса всей кривой равна [40].
Момент кривой относительно оси — момент () кривой относительно оси () равен следующей величине[41]:
- .
Центр тяжести кривой — точка плоскости такая, что если в ней находится материальная точка с массой всей кривой , то тогда статический момент этой точки относительно любой координатной оси равен статическому моменту ей кривой относительно той же оси[41].
По определению получаем, что
то есть имеем следующие формулы[41]:
Теорема Гульдина
Теорема Гульдина. Площадь поверхности вращения кривой около некоторой не пересекающей её оси равна произведению длины этой кривой и длины окружности, которая описана центром тяжести этой кривой[42].
Доказательство. Сравним формулу ординаты центра тяжести кривой (непрерывно дифференцируемой без особых точек)
с формулой площади поверхности вращения этой же кривой вокруг некоторой оси
- ,
имеем интересное соотношение
- ,
которое и доказывает теорему[42].
Если у кривой известно положение центра тяжести, то тогда по теорема Гульдина легко находится площадь поверхности вращения этой кривой[42].
Примеры
Площадь поверхности вращения окружности
Найдём площадь поверхности, полученной вращением окружности
не пересекающей ось , вокруг этой оси, то есть площадь поверхности тора. Поскольку центр окружности совпадает с её центром тяжести, имеем[42]:
- ,
Центр тяжести цепной линии
Найдём центр тяжести цепной линии, выраженной следующей формулой[42]:
Цепная линия симметрична относительно оси , поэтому момент
- ,
что легко доказать: выберем за начало отсчёта дуг пересечение цепной линии с осью , и пусть — длина цепной линии, тогда
- ,
так как — нечётная функция. И поскольку , то получаем первую координату центра тяжести[42]:
- .
Рассмотрим выражение для следующего момента
- ,
причём
- ,
где — площадь поверхности вращения цепной линии вокруг оси , то есть площадь поверхности катеноида. Но сама по себе площадь поверхности катеноида , следовательно, получаем следующее уравнение[42]:
- .
С другой стороны, назначенную длину цепной линии легко определить по формуле
-
- ,
откуда вытекает следующая формула для второй координаты центра тяжести[43]:
- .
Векторный элемент. Циркуляция
Рассмотрим в области трёхмерного пространства векторное поле, которое задано вектор-функцией , где — переменная точка. Циркуляцию векторного поля вдоль некоторой кусочно-гладкой кривой можно записать в виде криволинейного интеграла от скалярного произведения векторов
где — единичный вектор касательной к кривой (и к дуге ) в точке , — длина части кривой (дуги ), отсчитываемая от точки до переменной точки , и — соответственно скалярный и векторный элементы длины части кривой (дуги )[5][6][7][8].
В координатной форме, то есть в трёхмерной декартовой системе координат, получаем[6]:
- .
Элемент циркуляции — векторное произведение [44].
Если вектор-функцию интерпретировать как физическое силовое поле, то рассмотренная циркуляция такого векторного поля вдоль кривой есть механическая работа силы поля вдоль пути [5][44].
В электродинамике такие интегралы с встречаются при вычислении циркуляций векторов напряжённости электрического и магнитного полей
по замкнутому контуру, фигурирующих, в частности, в двух из четырёх уравнений Максвелла.
Элемент длины в приложениях при dl = dx (dy = 0)
Элемент объёма поперечных сечений
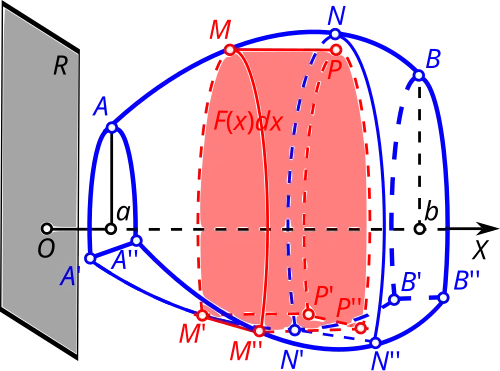
Пусть имеется произвольное тело, причём даны все площади его сечений, которые параллельны плоскости , проходящей через начало координат и перпендикулярной оси (см. рис.). Тогда объём этого тела равен следующему выражению:
- ,
где — расстояние от сечения до плоскости , — элемент оси , — элемент объёма поперечных сечений, и — крайние значения координаты [45].
Статические моменты и центр тяжести плоской фигуры
Определения

Пусть дана некоторая плоская фигура (см. рис.) — криволинейную трапецию, которая ограничена сверху кривой с явным уравнением неотрицательной функции , и по этой фигуре равномерно распределена масса с постоянной поверхностной плотностью . Без умаления общности положим , то есть масса произвольной части фигуры равна её площади, что всегда подразумевается, когда рассматривают статические моменты (или центр тяжести) плоской фигуры[46].
Вычислим статические моменты и криволинейной трапеции относительно осей координат. Рассмотрим произвольный элемент фигуры как бесконечно узкую вертикальную полоску (см. рис.). Аппроксимировав эту полоску прямоугольником, получаем её массу (и площадь) . Пусть масса полоски сосредоточена в её центре тяжести, то есть в центре прямоугольника, что не меняет величины статических моментов. Координаты этого центра тяжести , поскольку есть бесконечно малая второго порядка. Поэтому получаем следующие элементарные статические моменты[47]:
После суммирования этих элементарных моментов получаем статистические моменты
где [47].
Так же как и в случае статистических моментов кривой, теперь легко получить формулы для координат и центра тяжести плоской фигуры. Пусть — площадь (и масса) фигуры, тогда по основному свойству центра тяжести
откуда получаем следующие координаты центра тяжести[48]:
Теорема Гульдина
Вторая теорема Гульдина. Объём тела вращения плоской фигуры около некоторой не пересекающей её оси равен произведению площади этой фигуры и длины окружности, которая описана центром тяжести этой фигуры[49].
Доказательство. Сравним формулу ординаты центра тяжести плоской фигуры
с формулой тела вращения этой же кривой вокруг некоторой оси
- ,
имеем интересное соотношение
- ,
которое и доказывает теорему[49].
Эти формулы справедливы и для такой фигуры, которая ограничена снизу и сверху кривыми соответственно
в этом случае имеем следующие формулы статистических моментов[49][50]:
Преобразование формул для координат центра тяжести очевидны[49][51]:
Поскольку площадь такой фигуры есть
- ,
Примеры
Статические моменты и центр тяжести фигуры, ограниченной параболой
Найдём оба статических момента и , а также обе координаты и центра тяжести плоской фигуры — криволинейной трапеции, которая ограничена сверху параболой , снизу осью и сбоку прямой, параллельной оси ординат и соответствующей абсциссе . Исходя из уравнения параболы и формул
получаем следующие выражения для статистических моментов[49]:
Вычислим площадь криволинейной трапеции[49]:
Теперь по формулам
находим следующие выражения для координат центра тяжести[52]:
По второй теореме Гульдина найдём объём тела вращения данной фигуры вокруг прямой, которой принадлежит правая граница фигуры[52]:
Центр тяжести фигуры, ограниченной аркой циклоиды и осью абсцисс
Найдём координаты и центра тяжести фигуры, ограниченной аркой циклоиды
и осью абсцисс. Поскольку площадь и объём тела вращения данной фигуры около оси абсцисс соответственно равны
из соображений симметрии и по второй теореме Гульдина соответственно получаем[52]:
Примечания
- ↑ Полярные координаты, 1988.
- 1 2 3 4 5 6 7 Выгодский М. Я. Справочник по высшей математике, 1977, § 339. Дифференциал дуги, с. 572.
- 1 2 3 4 5 Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть I, 1971, Глава 11. Геометрические… § 1. Длина дуги кривой. 6. Дифференциал дуги, с. 366.
- 1 2 3 4 5 6 7 8 Ефимов Н. В. Дифференциальная геометрия, 1988, § 338. Длина дуги плоской линии, с. 195.
- 1 2 3 Иванов А. Б. Векторный анализ, 1988, с. 111.
- 1 2 3 4 Лаптев Г. Ф. Элементы векторного исчисления, 1975, Глава XIV. Векторное поле… § 3. Циркуляция поля… 2. Циркуляция вдоль линии, с. 245.
- 1 2 Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть II, 1980, Глава 7. Формулы Грина, Стокса, Остроградского, с. 174—175; 186; 199—200.
- 1 2 Циркуляция векторного поля, 1984.
- 1 2 Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 16.6. Плоские кривые, с. 274.
- ↑ Никольский С. М. Курс математического анализа. Т. I, 1983, § 6.7. Длина дуги кривой, с. 193.
- 1 2 Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Начальный курс, 1985, Глава 10. Геометрические приложения определенного интеграла. § 1. Длина дуги кривой. 5. Дифференциал дуги, с. 403.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 338. Длина дуги плоской линии, с. 570.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 334. Схема применения определенного интеграла, с. 563.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 451. Двойной интеграл, с. 761.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть I, 1971, Глава 11. Геометрические… § 1. Длина дуги кривой. 6. Дифференциал дуги, с. 366—367.
- 1 2 Никольский С. М. Курс математического анализа. Т. I, 1983, § 6.7. Длина дуги кривой, с. 194.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть I, 1971, Глава 11. Геометрические… § 1. Длина дуги кривой. 6. Дифференциал дуги, с. 367.
- 1 2 Выгодский М. Я. Справочник по высшей математике, 1977, § 340. Длина дуги и ее дифференциал в полярных координатах, с. 573.
- 1 2 Выгодский М. Я. Справочник по высшей математике, 1977, § 340. Длина дуги и ее дифференциал в полярных координатах, с. 574.
- ↑ Цилиндрические координаты, 1988.
- ↑ Сферические координаты, 1988.
- ↑ Соколов Д. Д. Цилиндрические координаты, 1985.
- ↑ Соколов Д. Д. Сферические координаты, 1985.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 339. Дифференциал дуги, с. 573.
- ↑ Ефимов Н. В. Высшая геометрия, 2004, 220, с. 511.
- ↑ Ефимов Н. В. Высшая геометрия, 2004, 216, с. 498.
- ↑ Ефимов Н. В. Дифференциальная геометрия, 1988, § 338. Длина дуги плоской линии, с. 195—196.
- 1 2 Ефимов Н. В. Высшая геометрия, 2004, 215, с. 493.
- ↑ Ефимов Н. В. Высшая геометрия, 2004, 215, с. 493—484.
- 1 2 Ефимов Н. В. Высшая геометрия, 2004, 215, с. 494.
- 1 2 Выгодский М. Я. Справочник по высшей математике, 1977, § 341. Площадь поверхности вращения, с. 575.
- ↑ Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.4. Площадь поверхности вращения, с. 506.
- ↑ Никольский С. М. Курс математического анализа. Т. I, 1983, § 10.4. Площадь поверхности тела вращения, с. 397.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 341. Площадь поверхности вращения, с. 575—576.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 341. Площадь поверхности вращения, с. 576.
- ↑ Никольский С. М. Курс математического анализа. Т. I, 1983, § 10.4. Площадь поверхности тела вращения, с. 398.
- 1 2 3 Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.4. Площадь поверхности вращения, с. 507.
- ↑ Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.5. Работа силы, с. 507—508.
- ↑ Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.5. Работа силы, с. 508.
- 1 2 3 4 5 Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.6. Вычисление статических моментов и центра тяжести кривой, с. 508.
- 1 2 3 Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.6. Вычисление статических моментов и центра тяжести кривой, с. 509.
- 1 2 3 4 5 6 7 Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.6. Вычисление статических моментов и центра тяжести кривой, с. 510.
- ↑ Кудрявцев Л. Д. Курс математического анализа, т. I, 1981, 32.6. Вычисление статических моментов и центра тяжести кривой, с. 511.
- 1 2 Лаптев Г. Ф. Элементы векторного исчисления, 1975, Глава XIV. Векторное поле… § 3. Циркуляция поля… 2. Циркуляция вдоль линии, с. 246.
- ↑ Выгодский М. Я. Справочник по высшей математике, 1977, § 336. Объем тела по поперечным сечениям, с. 567.
- ↑ Фихтенгольц Г. М. Курс математического анализа, т. I, 1968, 207. Нахождение статических моментов и центра тяжести плоской фигуры, с. 386.
- 1 2 Фихтенгольц Г. М. Курс математического анализа, т. I, 1968, 207. Нахождение статических моментов и центра тяжести плоской фигуры, с. 387.
- ↑ Фихтенгольц Г. М. Курс математического анализа, т. I, 1968, 207. Нахождение статических моментов и центра тяжести плоской фигуры, с. 387—388.
- 1 2 3 4 5 6 7 Фихтенгольц Г. М. Курс математического анализа, т. I, 1968, 207. Нахождение статических моментов и центра тяжести плоской фигуры, с. 388.
- ↑ Кудрявцев Л. Д. Курс математического анализа, т. II, 1981, 49.2. Физические приложения кратных интегралов, с. 231.
- 1 2 Кудрявцев Л. Д. Курс математического анализа, т. II, 1981, 49.2. Физические приложения кратных интегралов, с. 232.
- 1 2 3 Фихтенгольц Г. М. Курс математического анализа, т. I, 1968, 207. Нахождение статических моментов и центра тяжести плоской фигуры, с. 389.
Источники
- Выгодский М. Я. Справочник по высшей математике. Изд-е 12-е, стереотип. М.: «Наука», 1977. 871 с., ил.
- Ефимов Н. В. Высшая геометрия. 7-е изд. М.: Физматлит, 2004. 584 с. ISBN 5-9221-0267-2.
- Ефимов Н. В. Дифференциальная геометрия // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 189—197.
- Иванов А. Б. Векторный анализ // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 111—112.
- Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть I. 3-е изд., испр. и доп. М.: «Наука», 1971. 599 с. с илл. (Серия: «Курс высшей математики и математической физики». Выпуск 1 / Под ред. А. Н. Тихонова, В. А. Ильина, А. Г. Свешникова).
- Ильин В. А., Позняк Э. Г. Основы математического анализа. Часть II. 2-е изд., стереотипное. М.: «Наука», 1980. 447 с. с илл. (Серия: «Курс высшей математики и математической физики». Выпуск 2а / Под ред. А. Н. Тихонова, В. А. Ильина, А. Г. Свешникова).
- Ильин В. А., Садовничий В. А., Сендов Бл. Х. Математический анализ. Начальный курс. 2-е изд., перераб. / Под ред. А. Н. Тихонова. М.: Изд-во МГУ, 1985. 662 с. с илл.
- Кудрявцев Л. Д. Курс математического анализа (в двух томах): Учебник для студентов университетов и втузов. М.: «Высшая школа», 1981, т. I. 687 с., ил.
- Кудрявцев Л. Д. Курс математического анализа (в двух томах): Учебник для студентов университетов и втузов. М.: «Высшая школа», 1981, т. II. 584 с., ил.
- Лаптев Г. Ф. Элементы векторного исчисления. М.: Наука, 1975. 336 с., ил.
- Никольский С. М. Курс математического анализа. Т. I. 3-е изд., перераб. и доп. М.: «Наука», 1983. 464 с., ил.
- Полярные координаты // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 475.
- Соколов Д. Д. Сферические координаты // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 5 Слу—Я. М.: «Советская Энциклопедия», 1985. 1248 стб., ил. Стб. 293.
- Соколов Д. Д. Цилиндрические координаты // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 5 Слу—Я. М.: «Советская Энциклопедия», 1985. 1248 стб., ил. Стб. 819—820.
- Сферические координаты // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 572.
- Цилиндрические координаты // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 625.
- Циркуляция векторного поля // Воднев В. Т., Наумович А. Ф., Наумович Н. Ф. Математический словарь высшей школы: Общая часть / Под. ред. Ю. С. Богданова. Минск: «Высшая школа», 1984. 527 с., ил. С. 506—507.
- Фихтенгольц Г. М. Основы математического анализа, т. I. Изд. 6, стереотип. М.: «Наука», 1968. 440 с. с илл.