Область Рейнхарта

О́бласть Ре́йнхарта (англ. Reinhardt domain[1]) — понятие комплексного анализа, раздела математики, обобщение понятий шара и поликруга. Названа в честь немецкого математика Карла Рейнхарта[2][3][4][5].
Синонимы: кратно-круговая область[2][4][5]; -круговая область (англ. multicircular domain)[3][1].
Логарифмически выпуклая область Рейнхарта обладает следующим свойством: любая такая область в комплексном пространстве есть внутренность множества точек абсолютной сходимости (другими словами, собственно область сходимости) некоторого степенного ряда по переменным
и обратно: область сходимости любого степенного ряда по
есть логарифмически выпуклая полная область Рейнхарта с центром [2].
Область Рейнхарта есть частный случай круговой области[2][6], а также кратно-кругообразной области[5].
Определение области Рейнхарта
Область Рейнхарта (англ. Reinhardt domain) — область комплексного пространства , , имеющая такое свойство, что вместе с каждой точкой
в области лежат также и все точки следующего вида[2][3][4][7][1]:
или
или
При получаем[2][3][8][9][5][1]:
Присутствующая в определении точка называется центром области Рейнхарта[2][3][4][7].
Область Рейнхарта имеет следующие автоморфизмы[4][7]:
Теорема. Для связной области Рейнхарта , причём начало координат , голоморфная в функция может быть разложена на области в ряд по степеням
- ,
причём этот ряд сходится нормально на области и это разложение единственно[10].
Указанный в теореме ряд в общем случае будет сходиться и за пределами области Рейнхарта, имея своей областью сходимости соответствующую полную область Рейнхарта, в которой содержится исходная область Рейнхарта . Но не любая полная область служит такой областью сходимости ряда[7].
Полная область Рейнхарта
Полная область Рейнхарта (англ. complete Reinhardt domain) — область Рейнхарта , в которой с каждой точкой
лежит следующий поликруг[2][3][4][7][1]:
или
или
При получаем[1]:
Полная область Рейнхарта звездообразна относительно своего центра [2]. Примеры полных областей Рейнхарта: шар и поликруг[2][3][11]. В случае приведём следующие примеры[3][1]:
- неполные области Рейнхарта — кольца
- ,
- полные области Рейнхарта — круги
Полная область Рейнхарта , пересекаясь с любой плоскостью
вырезает в ней полный круг[12].
Область Рейнхарта — наиболее важный вид кратно-кругообразной области. В том случае, когда начало координат принадлежит области Рейнхарта , её аналитическое расширение — выпуклая область Рейнхарта . Так полученная область называется рейнхартовым аналитическим расширением области[5].
Относительно полная область Рейнхарта
Относительно полная область Рейнхарта — область Рейнхарта
которая при постоянном либо совсем не пересекается с плоскостью , либо с каждой точкой включает и все такие точки , для которых
а остальные координаты те же самые, что у , причём это условие выполняется для всех [13].
Другими словами, когда область Рейнхарта ни с какой плоскостью не пересекается, условие относительной полноты никаких ограничений на такую область Рейнхарта вообще не накладывает. И только при пересечении области Рейнхарта с каждой из плоскостей возникает дополнительное условие[14].
Логарифмически выпуклая область Рейнхарта
Логарифмически выпуклая область Рейнхарта (англ. logarithmically convex Reinhardt domain) — область Рейнхарта как логарифмически выпуклое множество[2].
Логарифмически выпуклая область Рейнхарта обладает следующим свойством: любая такая область в комплексном пространстве есть внутренность множества точек абсолютной сходимости (другими словами, собственно область сходимости) некоторого степенного ряда по переменным
и обратно: область сходимости любого степенного ряда по
есть логарифмически выпуклая полная область Рейнхарта с центром [2].
Диаграмма Рейнхарта
Поскольку центр области Рейнхарта всегда можно сдвинуть в начало координат комплексного пространства , то можно считать без ограничения общности, что . Область Рейнхарта с так упрощённым описанием инвариантна относительно следующего преобразования:
то есть с любой своей точкой область Рейнхарта включает также и все точки с теми же и всевозможными аргументами[2][3][1].
Отсюда следует, что можно рассмотреть отображение
-мерного пространства в -мерное пространство , точнее говоря, в абсолютный октант [3]}[11].
Абсолютный октант — восьмая часть -мерного пространства :
- ,
где — полуось неотрицательных чисел[15][11].
Диаграмма, или изображение, Рейнхарта области (англ. trace ) — множество точек абсолютного октанта , в которое переводит область при отображении [16][11][1].
В частности, в случае полной области Рейнхарта диаграмма Рейнхарта есть область и обладает тем свойством, что вместе с каждой точкой в области лежит и весь прямоугольный параллелепипед, или призма, [16][11].
Область Рейнхарта полностью характеризуется своей диаграммой Рейнхарта. Например, если связно, то и связно (и наоборот), если открыто, то и открыто[16][1].
В случае области Рейнхарта, или двоякокруглой области, расположенной в двумерном комплексном пространстве двух комплексных переменных и , абсолютный октант есть абсолютная четверть-плоскость с координатами и [11].
Свойство диаграммы Рейнхарта понижать размерность пространства на единиц делает изображение Рейнхарта наглядным для и . На рисунках ниже показаны диаграммы Рейнхарта для и шара и поликруга ; для поликруга изображены множества его границы и его остов [16].
- Диаграммы Рейнхарта шара и поликруга
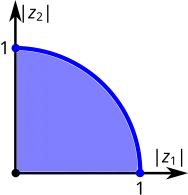 Диаграмма Рейнхарта шара для
Диаграмма Рейнхарта шара для Диаграмма Рейнхарта шара для
Диаграмма Рейнхарта шара для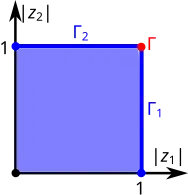 Диаграмма Рейнхарта бикруга для
Диаграмма Рейнхарта бикруга для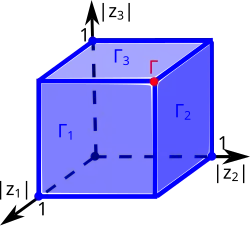 Диаграмма Рейнхарта трикруга для
Диаграмма Рейнхарта трикруга для
Пример
Рассмотрим некоторое множество с диаграммой Рейнхарта , показанной на рисунке ниже слева. Это множество не относится к логарифмически выпуклым. Логарифмический образ этого множества показана на рисунке ниже справа[17].
- Диаграмма Рейнхарта и логарифмический образ в C×C
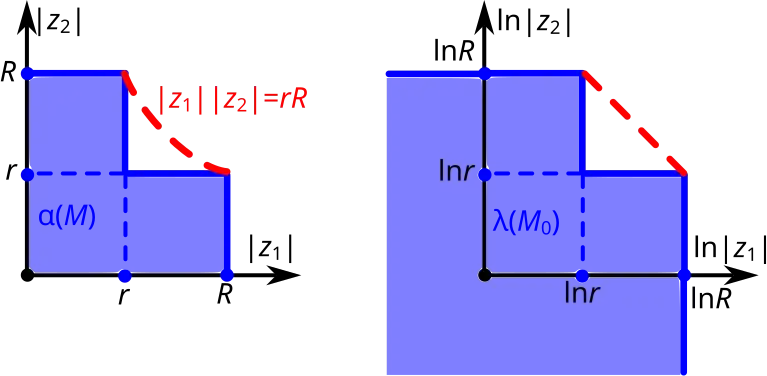 Диаграмма Рейнхарта логарифмически выпуклой оболочки некоторого множества в и выпуклая оболочка его логарифмического образа
Диаграмма Рейнхарта логарифмически выпуклой оболочки некоторого множества в и выпуклая оболочка его логарифмического образа
Прообраз выпуклой оболочки логарифмического образа есть логарифмически выпуклая оболочка множества . Диаграммы Рейнхарта оболочки и исходного множества отличаются только сегментом, граница которого показан пунктиром на рисунке. Этот сегмент получен как прообраз треугольника, дополняющего логарифмический образ до выпуклости. Гипотенуза этого треугольника есть отрезок прямой
- ,
поэтому сегмент выпуклости, добавленный к диаграмме Рейнхарта , ограничен частью следующей гиперболы[17]:
- .
Круговая область
Область Рейнхарта естественным образом обобщается на круговую область[2].
Круговая область — область комплексного пространства , , имеющая такое свойство, что вместе с каждой точкой в области лежат и все точки вида
другими словами, все точки окружности на комплексной прямой, проходящей через заданную точку и любую точку , с центром и следующим радиусом[2][6]:
- .
При получаем[18]:
Присутствующая в определении точка называется центром круговой области[6].
Синоним: круговое точечное множество[19].
Круговая область есть частный случай области Хартогса[19].
Теорема. Для связной круговой области , причём начало координат , голоморфная в функция может быть разложена на области в ряд по однородным многочленам
- ,
где — однородный многочлен степени по переменным , причём этот ряд сходится нормально на области и это разложение единственно[18].
Полная круговая область — круговая область , в которой с каждой точкой лежит весь следующий круг[2][6]:
При достаточно простое преобразование комплексного пространства вида
переводит круговую область в область Хартогса, причём указанное преобразование определено только на области без начала координат , поскольку оно имеет особенность при [20].
Примечания
- 1 2 3 4 5 6 7 8 9 10 11 Jaap Korevaar, Jan Wiegerinck. Several Complex Variables, 2011, 2.3 Multiple power series and multicircular domains, p. 30.
- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Соломенцев Е. Д. Кратно круговая область, 1982.
- 1 2 3 4 5 6 7 8 9 10 11 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 16.
- 1 2 3 4 5 6 Владимиров В. С. Методы теории функций многих комплексных переменных, 1964, § 7. Голоморфные отображения, б. Группа автоморфизмов, с. 63.
- 1 2 3 4 5 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 8. Кратно-кругообразные области, с. 114.
- 1 2 3 4 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 18.
- 1 2 3 4 5 Фукс Б. А. Теория аналитических функций многих комплексных переменных, 1962, § 3. Представление голоморфного функционального элемента степенным рядом, 3. n-круговые области, с. 57.
- ↑ Хёрмандер, Ларс Введение в теорию функций нескольких комплексных переменных, 1968, 2.4. Степенные ряды и области Рейихарта, с. 57.
- ↑ Мальгранж Б. Лекции по теории функций нескольких комплексных переменных, 1969, § 2. Области Рейнхарта и круговые области, с. 12.
- ↑ Мальгранж Б. Лекции по теории функций нескольких комплексных переменных, 1969, § 2. Области Рейнхарта и круговые области, с. 12—13.
- 1 2 3 4 5 6 Фукс Б. А. Теория аналитических функций многих комплексных переменных, 1962, § 3. Представление голоморфного функционального элемента степенным рядом, 3. n-круговые области, с. 58.
- ↑ Фукс Б. А. Теория аналитических функций многих комплексных переменных, 1962, § 3. Представление голоморфного функционального элемента степенным рядом, 3. n-круговые области, с. 57—58.
- ↑ Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 8. Другие ряды, с. 50—51.
- ↑ Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 8. Другие ряды, с. 51.
- ↑ Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 16—17.
- 1 2 3 4 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 17.
- 1 2 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 7. Степенные ряды, с. 44.
- 1 2 Мальгранж Б. Лекции по теории функций нескольких комплексных переменных, 1969, § 2. Области Рейнхарта и круговые области, с. 18.
- 1 2 Бохнер С., Мартин У. Т. Функции многих комплексных переменных, 1951, Глава IV. Аналитическое расширение. § 7. Кругообразные области, с. 110.
- ↑ Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 2. Простейшие области, с. 19.
Источники
- Бохнер С., Мартин У. Т. Функции многих комплексных переменных / Пер. с англ. Б. А. Фукса. М.: «Издательство иностранной литературы», 1951. 300 с.: ил. [Salomon Bochner, William Ted Martin, Several Complex Variables. Princeton, 1948.]
- Владимиров В. С. Методы теории функций многих комплексных переменных / Предисловие академика Н. Н. Боголюбова. М.: «Наука», 1964. 411 с.: ил.
- Мальгранж Б. Лекции по теории функций нескольких комплексных переменных / Пер. с англ. Ю. В. Линника. М.: «Наука», 1969. 119 с.: ил. [Malgrange B. Lectures on the theory of functions of several complex variables.]
- Соломенцев Е. Д. Кратно круговая область // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 3 Коо—Од. М.: «Советская энциклопедия», 1982. 1184 стб., ил. Стб. 88—89.
- Соломенцев Е. Д. Поликруг // Математическая энциклопедия: Гл. ред. И. М. Виноградов, т. 4 Ок—Сло. М.: «Советская Энциклопедия», 1984. 1216 стб., ил. Стб. 405—406.
- Фукс Б. А. Теория аналитических функций многих комплексных переменных: 2-е изд., перераб. и доп. М.: Физматлит, 1962. 419 с.
- Хёрмандер, Ларс. Введение в теорию функций нескольких комплексных переменных / Пер. с англ. Е. М. Чирки, под ред. Б. В. Шабата. М.: «Мир», 1968. 279 с.
- Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.
- Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.