Список моделей многогранников Веннинджера

В данной статье содержится список таких однородных многогранников и звёздчатых многогранников, которые упоминаются в книге «Модели многогранников» Магнуса Веннинджера.

Книга «Модели многогранников» Веннинджера — руководство по построению физических (например, бумажных) моделей многогранников. Книга содержит короткое описание связанной с многогранниками теории, чертежи элементов граней многогранников, рекомендации по построению моделей многогранников. Книга описывает модели непризматических однородных многогранников всех (75-и) видов однородных многогранников и модели 44-х звёздчатых форм выпуклых правильных и полуправильных многогранников (всего — 75+44 = 119).

Список создан как дань уважения работе Веннинджера и для предоставления возможности создания ссылок на 119 пронумерованных в книге моделей.

Пусть N — номер описаной в книге модели. Тогда, чтобы поставить ссылку на описанную в книге модель, укажите либо текст вида «модель Веннинджера номер N», либо текст вида WN, где W — первая буква фамилии Веннинджера (англ. Wenninger).

Многогранники перечислены в пяти таблицах:

  1. правильные многогранники (от W1 до W5);
  2. полуправильные многогранники (от W6 до W18);
  3. правильные звёздчатые многогранники (W20, W21, W22, W41);
  4. звёздчатые формы многогранников и соединения многогранников (от W19 до W66);
  5. однородные звёздчатые многогранники (от W67 до W119).

Четыре правильных звёздчатых многогранника приведены дважды, поскольку принадлежат и однородным многогранникам, и звёздчатым формам.

Правильные многогранники (плато́новы тела) (модели от W1 до W5)

Номер Название Рисунок Имя двойственного Рисунок двойственного Символ
Витхоффа		 Вершинная фигура
и символ Шлефли		 Группа симметрии U# K# V E F Грани по типам
1 Тетраэдр Тетраэдр 3|2 3
{3,3}		 Td U01 K06 4 6 4 4{3}
2 Октаэдр Гексаэдр 4|2 3
{3,4}		 Oh U05 K10 6 12 8 8{3}
3 Гексаэдр (Куб) Октаэдр 3|2 4
{4,3}		 Oh U06 K11 8 12 6 6{4}
4 Икосаэдр 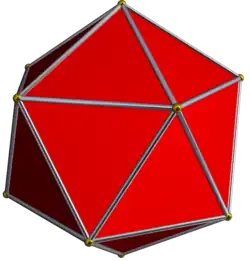Додекаэдр 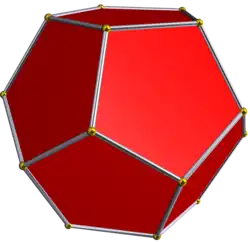5|2 3
{3,5}		 Ih U22 K27 12 30 20 20{3}
5 Додекаэдр Икосаэдр 3|2 5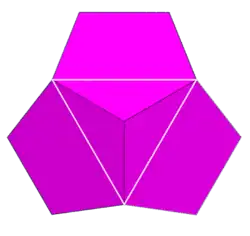
{5,3}		 Ih U23 K28 20 30 12 12{5}

Архимедовы тела (полуправильные) (модели от W6 до W18)

Номер Название Рисунок Имя двойственного Рисунок двойственного Символ
Витхоффа		 Вершинная фигура
и символ Шлефли		 Группа симметрии U# K# V E F Грани по типам
6 Усечённый тетраэдр 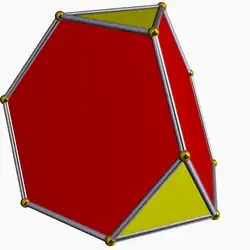триакистетраэдрTriakis tetrahedron 2 3|3
3.6.6		 Td U02 K07 12 18 8 4{3} + 4{6}
7 Усечённый октаэдр 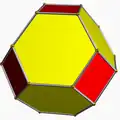тетракисгексаэдрTetrakis hexahedron 2 4|3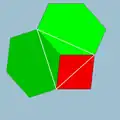
4.6.6		 Oh U08 K13 24 36 14 6{4} + 8{6}
8 Усечённый гексаэдр 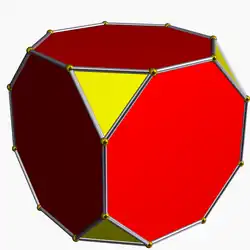триакисоктаэдрTriakis octahedron 2 3|4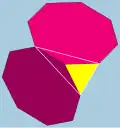
3.8.8		 Oh U09 K14 24 36 14 8{3} + 6{8}
9 Усечённый икосаэдр пентакисдодекаэдрPentakis dodecahedron 2 5|3
5.6.6		 Ih U25 K30 60 90 32 12{5} + 20{6}
10 Усечённый додекаэдр триакисикосаэдрTriakis icosahedron 2 3|5
3.10.10		 Ih U26 K31 60 90 32 20{3} + 12{10}
11 Кубооктаэдр 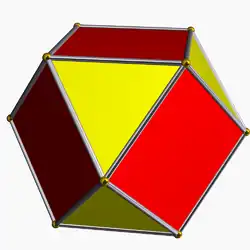ромбододекаэдрRhombic dodecahedron 2|3 4
3.4.3.4		 Oh U07 K12 12 24 14 8{3} + 6{4}
12 Икосододекаэдр 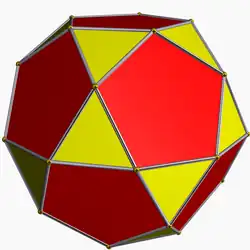ромботриаконтаэдрRhombic triacontahedron 2|3 5
3.5.3.5		 Ih U24 K29 30 60 32 20{3} + 12{5}
13 Ромбокубооктаэдр 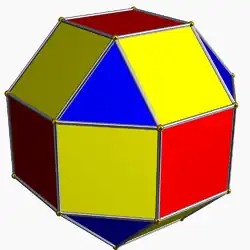дельтоидальный икоситетраэдрDeltoidal icositetrahedron 3 4|2
3.4.4.4		 Oh U10 K15 24 48 26 8{3}+(6+12){4}
14 Ромбоикосидодекаэдр дельтоидальный гексеконтаэдрDeltoidal hexecontahedron 3 5|2
3.4.5.4		 Ih U27 K32 60 120 62 20{3} + 30{4} + 12{5}
15 Усечённый кубооктаэдр
(Большой ромбокубооктаэдр)		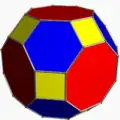 ГекзакисоктаэдрDisdyakis dodecahedron 2 3 4|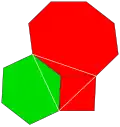
4.6.8		 Oh U11 K16 48 72 26 12{4} + 8{6} + 6{8}
16 Ромбоусечённый икосододекаэдр
(Большой ромбоикосододекаэдр)		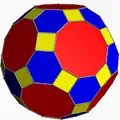 ГекзакисикосаэдрDisdyakis triacontahedron 2 3 5|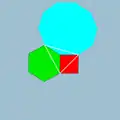
4.6.10		 Ih U28 K33 120 180 62 30{4} + 20{6} + 12{10}
17 Плосконосый куб 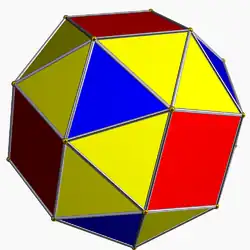пентагональный икоситетраэдрPentagonal icositetrahedron |2 3 4
3.3.3.3.4		 O U12 K17 24 60 38 (8 + 24){3} + 6{4}
18 Плосконосый додекаэдр пентагональный гексеконтаэдрPentagonal hexecontahedron |2 3 5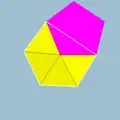
3.3.3.3.5		 I U29 K34 60 150 92 (20 + 60){3} + 12{5}

Тела Кеплера — Пуансо (правильные звёздчатые многогранники) (модели W20, W21, W22 и W41)

Номер Название Рисунок Имя двойственного Рисунок двойственного Символ
Витхоффа		 Вершинная фигура
и символ Шлефли		 Группа симметрии U# K# V E F Грани по типам
20 Малый звёздчатый додекаэдр Большой додекаэдр 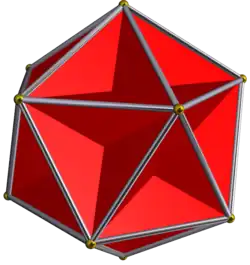5|25/2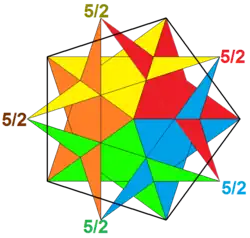
{5/2,5}		 Ih U34 K39 12 30 12 12{5/2}
21 Большой додекаэдр Малый звёздчатый додекаэдр 5/2|2 5
{5,5/2}		 Ih U35 K40 12 30 12 12{5}
22 Большой звёздчатый додекаэдр Большой икосаэдр 3|25/2
{5/2,3}		 Ih U52 K57 20 30 12 12{5/2}
41 Большой икосаэдр
(16-я звёздчатая форма икосаэдра)		 Большой звёздчатый додекаэдр 5/2|2 3
{3,5/2}		 Ih U53 K58 12 30 20 20{3}

Звёздчатые многогранники (модели от W19 до W66)

Звёздчатый октаэдр

Номер Название Группа симметрии Рисунок Грани
2 Октаэдр
(правильный)		 Oh
19 Звёздчатый октаэдр
(Соединение двух тетраэдров)		 Oh

Звёздчатые формы додекаэдра

Номер Название Группа симметрии Рисунок Грани
5 Додекаэдр (правильный) Ih
20 Малый звёздчатый додекаэдр(правильный)
(1-я звёздчатая форма додекаэдра)		 Ih
21 Большой додекаэдр (правильный)
(2-я звёздчатая форма додекаэдра)		 Ih
22 Большой звёздчатый додекаэдр(правильный)
(3-я звёздчатая форма додекаэдра)		 Ih

Звёздчатые формы икосаэдра

Номер Название Группа симметрии Рисунок Грани
4 Икосаэдр (правильный) Ih
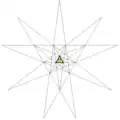23 Соединение пяти октаэдров
(1-я составная форма звёздчатого икосаэдра)		 Ih
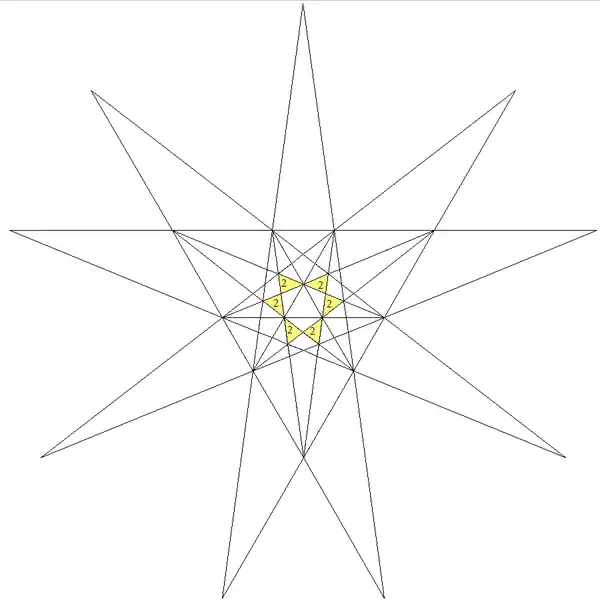24 Соединение пяти тетраэдров
(2-я составная форма звёздчатого икосаэдра)		 I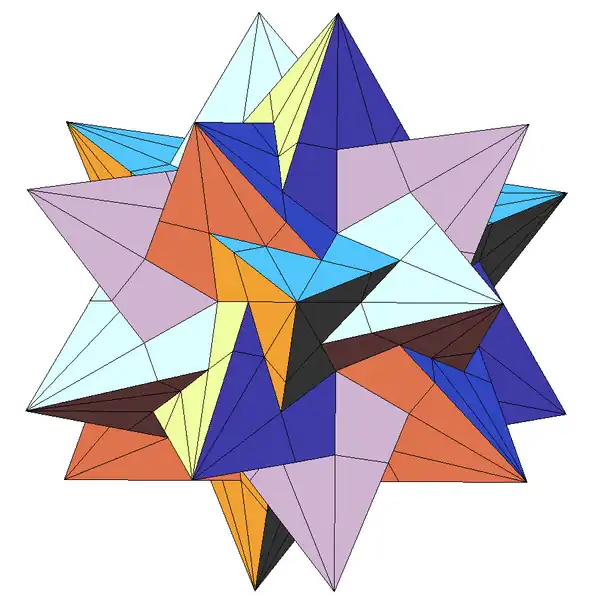
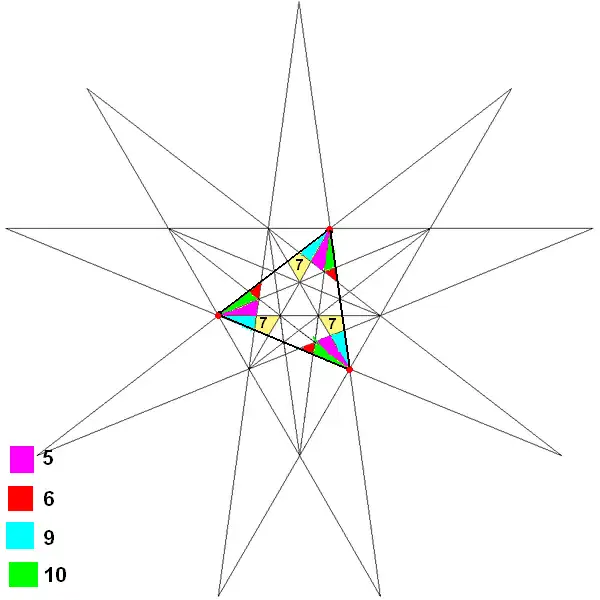25 Соединение десяти тетраэдров
(3-я составная форма звёздчатого икосаэдра)		 Ih
26 Малый триамбический икосаэдр
(1-я звёздчатая форма икосаэдра)
(Триакисикосаэдр)		 Ih
27 2-я звёздчатая форма икосаэдра Ih
28 Выемчатый додекаэдр
(3-я звёздчатая форма икосаэдра)		 Ih
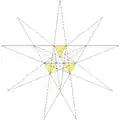29 4-я звёздчатая форма икосаэдра Ih
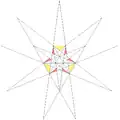30 5-я звёздчатая форма икосаэдра Ih
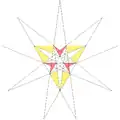31 6-я звёздчатая форма икосаэдра Ih
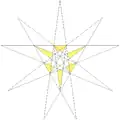32 7-я звёздчатая форма икосаэдра Ih
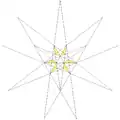33 8-я звёздчатая форма икосаэдра Ih
34
Большой триамбикикосаэдр


(9-я звёздчатая форма икосаэдра)

 Ih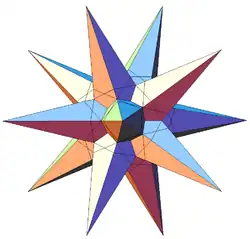
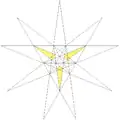35 10-я звёздчатая форма икосаэдра I
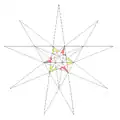36 11-я звёздчатая форма икосаэдра I
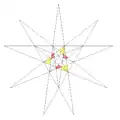37 12-я звёздчатая форма икосаэдра Ih
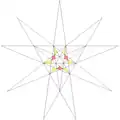38 13-я звёздчатая форма икосаэдра I
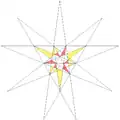39 14-я звёздчатая форма икосаэдра I
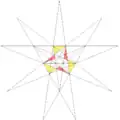40 15-я звёздчатая форма икосаэдра I
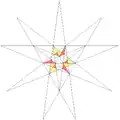41 Большой икосаэдр (правильный)
(16-я звёздчатая форма икосаэдра)		 Ih
42 Ехиднаэдр
(Завершающая, 17-я звёздчатая форма икосаэдра)		 Ih

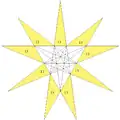Звёздчатые формы кубооктаэдра

Номер Название Группа симметрии Рисунок Грани (октаэдральные плоскости) Грани (кубические плоскости)
11 Кубооктаэдр (правильный) Oh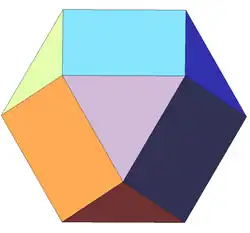
43 Соединение куба и октаэдра
(1-я звёздчатая форма кубооктаэдра)		 Oh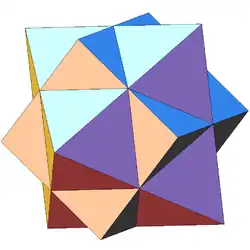
44 2-я звёздчатая форма кубооктаэдра Oh
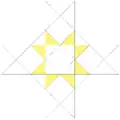45 3-я звёздчатая форма кубооктаэдра Oh
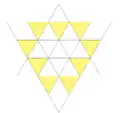46 4-я звёздчатая форма кубооктаэдра Oh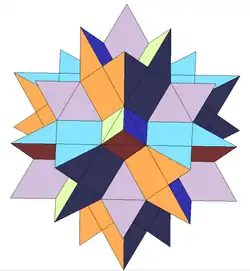

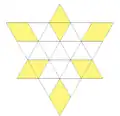Звёздчатые формы икосододекаэдра

Номер Название Группа симметрии Рисунок Грани (икосоэдральные плоскости) Грани (додекаэдральные плоскости)
12 Икосододекаэдр
(правильный)		 Ih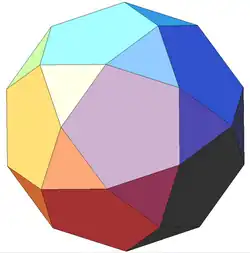
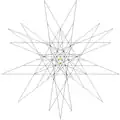
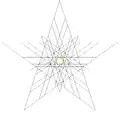
47 1-я звёздчатая форма икосододекаэдра
Соединение додекаэдра и икосаэдра		 Ih
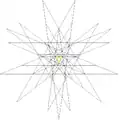48 2-я звёздчатая форма икосододекаэдра Ih
49 3-я звёздчатая форма икосододекаэдра Ih
50 4-я звёздчатая форма икосододекаэдра
(Соединение малого звёздчатого додекаэдра
и триакисикосаэдра)		 Ih
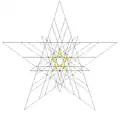51 5-я звёздчатая форма икосододекаэдра
(Соединение малого звёздчатого додекаэдра
и пяти октаэдров)		 Ih
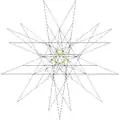52 6-я звёздчатая форма икосододекаэдра Ih
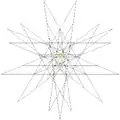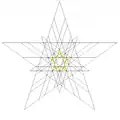53 7-я звёздчатая форма икосододекаэдра Ih
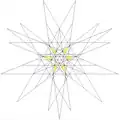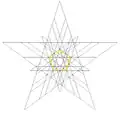54 8-я звёздчатая форма икосододекаэдра
(Соединение пяти тетраэдров
и большого додекаэдра)		 I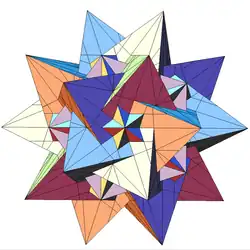
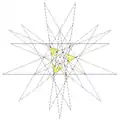55 9-я звёздчатая форма икосододекаэдра Ih
56 10-я звёздчатая форма икосододекаэдра Ih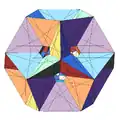
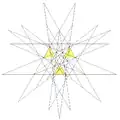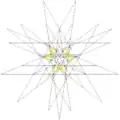
57 11-я звёздчатая форма икосододекаэдра Ih
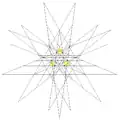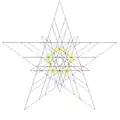58 12-я звёздчатая форма икосододекаэдра Ih
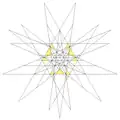59 13-я звёздчатая форма икосододекаэдра Ih
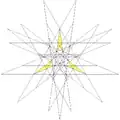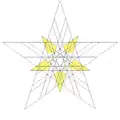60 14-я звёздчатая форма икосододекаэдра Ih
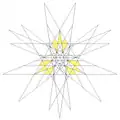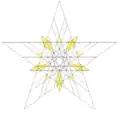61 Соединение большого звёздчатого додекаэдра и большого икосаэдра Ih
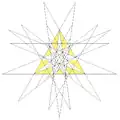62 15-я звёздчатая форма икосододекаэдра Ih
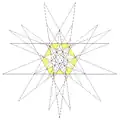63 16-я звёздчатая форма икосододекаэдра Ih
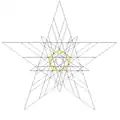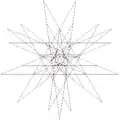
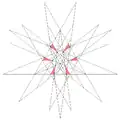
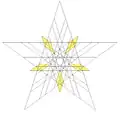
64 17-я звёздчатая форма икосододекаэдра Ih
65 18-я звёздчатая форма икосододекаэдра Ih
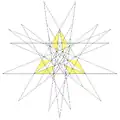66 19-я звёздчатая форма икосододекаэдра Ih

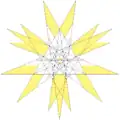Однородные невыпуклые тела (модели от W67 до W119)

Номер Название Рисунок Название
двойственного		 Рисунок двойственного Символ
Витхоффа		 Вершинная фигура Группа симметрии U# K# V E F Грани по типам
67Тетрагемигексаэдр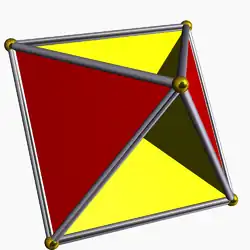Тетрагемигексакрон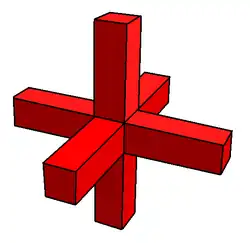3/23|2
4.3/2.4.3		TdU04K0961274{3}+3{4}
68Октагемиоктаэдр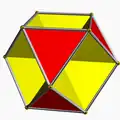Октагемиоктакрон3/23|3
6.3/2.6.3		OhU03K081224128{3}+4{6}
69Малый кубокубооктаэдр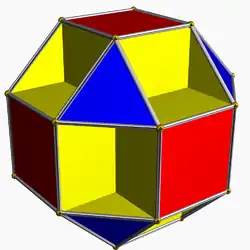Малый гексакронный икосотетраэдр3/24|4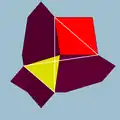
8.3/2.8.4		OhU13K182448208{3}+6{4}+6{8}
70Малый битригональный икосододекаэдрМалый триамбический икосаэдр3|5/23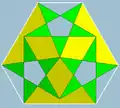
(5/2.3)3		IhU30K3520603220{3}+12{5/2}
71Малый икосоикосододекаэдрМалый икосакронный гексаконтаэдр5/23|3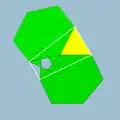
6.5/2.6.3		IhU31K36601205220{3}+12{5/2}+20{6}
72Малый додекоикосододекаэдрМалый додекакронный гексаконтаэдр3/25|5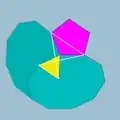
10.3/2.10.5		IhU33K38601204420{3}+12{5}+12{10}
73Додекододекаэдр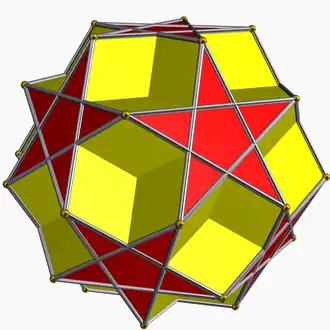Средний ромбический триаконтаэдр2|5/25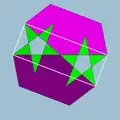
(5/2.5)2		IhU36K4130602412{5}+12{5/2}
74Малый ромбододекаэдрМалый
ромбододекакрон		25/25|
10.4.10/9.4/3		IhU39K44601204230{4}+12{10}
75Усечённый большой додекаэдр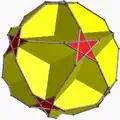Малый звёздчатый пентакисдодекаэдр25/2|5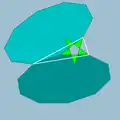
10.10.5/2		IhU37K4260902412{5/2}+12{10}
76РомбододекододекаэдрСредний дельтоидный гексаконтаэдр5/25|2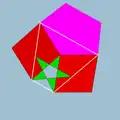
4.5/2.4.5		IhU38K43601205430{4}+12{5}+12{5/2}
77Большой кубокубооктаэдрБольшой гексакронный икосотетраэдр3 4|4/3
8/3.3.8/3.4		OhU14K192448208{3}+6{4}+6{8/3}
78КубогемиоктаэдрГексагемиоктакрон4/34|3
6.4/3.6.4		OhU15K201224106{4}+4{6}
79Кубоусечённый кубооктаэдр
(Кубооктоусечённый кубооктаэдр)		Тетрадиакисгексаэдр4/33 4|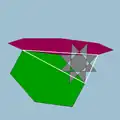
8/3.6.8		OhU16K214872208{6}+6{8}+6{8/3}
80Битригональный додекаэдр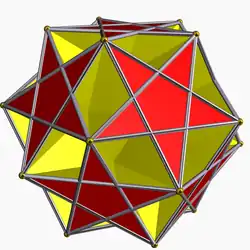Средний триамбикикосаэдр ↗ Перенаправить на Большой триамбикикосаэдр3|5/35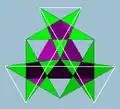
(5/3.5)3		IhU41K4620602412{5}+12{5/2
81Большой битригональный додекоикосододекаэдрБольшой битриагональный додекакронный гексаконтаэдр3 5|5/3
10/3.3.10/3.5		IhU42K47601204420{3}+12{5}+12{10/3}
82Малый битригональный додекоикосододекаэдр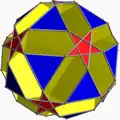Малый битриагональный додекакронный гексаконтаэдр5/33|5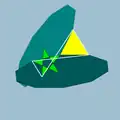
10.5/3.10.3		IhU43K48601204420{3}+12{5/2}+12{10}
83ИкосододекододекаэдрСредний икосакронный
гексаконтаэдр		5/35|3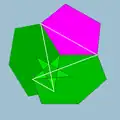
6.5/3.6.5		IhU44K49601204412{5}+12{5/2}+20{6}
84Икосоусечённый додекододекаэдр
(Икосододекоусечённый икосододекаэдр)		Тридиакисикосаэдр5/33 5|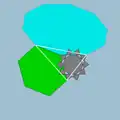
10/3.6.10		IhU45K501201804420{6}+12{10}+12{10/3}
85Невыпуклый большой ромбокубооктаэдр
(Квазиромбокубооктаэдр)		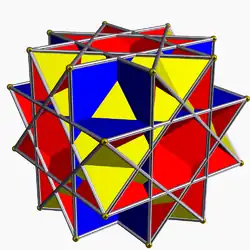Большой дельтоидный икосотетраэдр3/24|2
4.3/2.4.4		OhU17K222448268{3}+(6+12){4}
86Малый ромбогексаэдр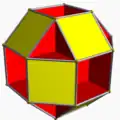Малый ромбогексакрон3/22 4|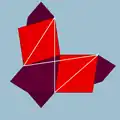
4.8.4/3.8		OhU18K2324481812{4}+6{8}
87Большой битригональный икосододекаэдрБольшой триамбикикосаэдр3/2|3 5
(5.3.5.3.5.3)/2		IhU47K5220603220{3}+12{5}
88Большой икосоикосододекаэдрБольшой икосакронный гексаконтаэдр3/25|3
6.3/2.6.5		IhU48K53601205220{3}+12{5}+20{6}
89Малый икосогемидодекаэдрМалый икосогемидодекакрон3/23|5
10.3/2.10.3		IhU49K5430602620{3}+6{10}
90Малый додекоикосаэдрМалый додекоикосакрон3/23 5|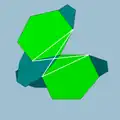
10.6.10/9.6/5		IhU50K55601203220{6}+12{10}
91Малый додекогемидодекаэдр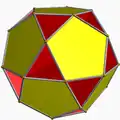Малый додекогемидодекакрон5/45|5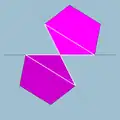
10.5/4.10.5		IhU51K5630601812{5}+6{10}
92Звёздчатый усечённый гексаэдр
(Квазиусечённый гексаэдр)		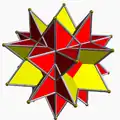Большой триакисоктаэдр2 3|4/3
8/3.8/3.3		OhU19K242436148{3}+6{8/3}
93Большой усечённый кубооктаэдр
(Квазиусечённый кубооктаэдр)		Большой дисдиакисдодекаэдр4/32 3|
8/3.4.6		OhU20K2548722612{4}+8{6}+6{8/3}
94Большой икосододекаэдр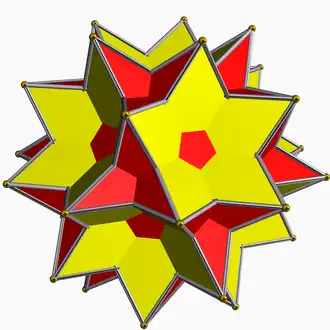Большой ромбический тридцатигранник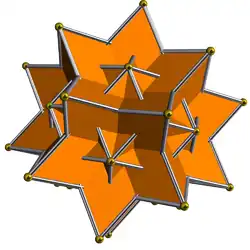2|5/23
(5/2.3)2		IhU54K5930603220{3}+12{5/2}
95Усечённый большой икосаэдр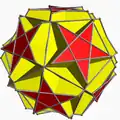Большой звёздчатый пентакисдодекаэдр25/2|3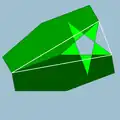
6.6.5/2		IhU55K6060903212{5/2}+20{6}
96РомбоикосаэдрРомбоикоакрон25/23|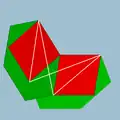
6.4.6/5.4/3		IhU56K61601205030{4}+20{6}
97Малый звёздчатый усечённый додекаэдр
(Квазиусечённый звёздчатый додекаэдр)		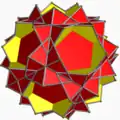Большой пентакисдодекаэдр2 5|5/3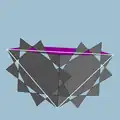
10/3.10/3.5		IhU58K6360902412{5}+12{10/3}
98Усечённый додекадодекаэдр
(Квазиусечённый додекаэдр)		Средний дисдиакистриаконтаэдр5/32 5|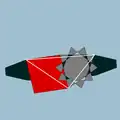
10/3.4.10		IhU59K641201805430{4}+12{10}+12{10/3}
99Большой додекоикосододекаэдрБольшой додекакроникгексаконтаэдр5/23|5/3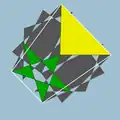
10/3.5/2.10/3.3		IhU61K66601204420{3}+12{5/2}+12{10/3 }
100Малый додекогемиикосаэдрМалый додекогемиикосакрон5/35/2|3
6.5/3.6.5/2		IhU62K6730602212{5/2}+10{6}
101Большой додекоикосаэдр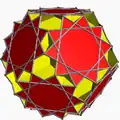Большой додекоикосакрон5/35/23|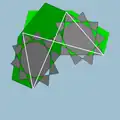
6.10/3.6/5.10/7		IhU63K68601203220{6}+12{10/3}
102Большой додекогемиикосаэдр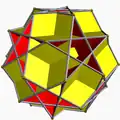Большой додекогемиикосакрон5/45|3
6.5/4.6.5		IhU65K7030602212{5}+10{6}
103Большой ромбогексаэдр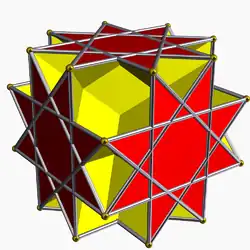Большой ромбогексакрон4/33/22|
4.8/3.4/3.8/5		OhU21K2624481812{4}+6{8/3}
104Большой звёздчатый усечённый додекаэдр
(Квазиусечённый большой звёздчатый додекаэдр)		Большой триакисикосаэдр2 3|5/3
10/3.10/3.3		IhU66K7160903220{3}+12{10/3}
105Невыпуклый большой ромбоикосододекаэдр
(Квазиромбоикосододекаэдр)		Большой дельтоидальный гексаконтаэдр5/33|2
4.5/3.4.3		IhU67K72601206220{3}+30{4}+12{5/2}
106Большой икосогемидодекаэдрБольшой икосогемидодекакрон3 3|5/3
10/3.3/2.10/3.3		IhU71K7630602620{3}+6{10/3}
107Большой додекогемидодекаэдр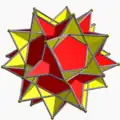Большой додекогемидодекакрон5/35/2|5/3
10/3.5/3.10/3.5/2		IhU70K7530601812{5/2}+6{10/3}
108Большой усечённый икосододекаэдр
(Большой квазиусечённый икосододекаэдр)		Большой дисдиакистриаконтаэдр5/32 3|
10/3.4.6		IhU68K731201806230{4}+20{6}+12{10/3}
109Большой ромбододекаэдрБольшой ромбододекакрон3/25/32|
4.10/3.4/3.10/7		IhU73K78601204230{4}+12{10/3}
110Малый плосконосый икосоикосододекаэдр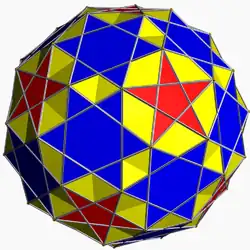Малый шестиугольный гексаконтаэдр|5/23 3
3.3.3.3.3.5/2		IhU32K3760180112(40+60){3}+12{5/2}
111Плосконосый додекододекаэдрСредний пятиугольный гексаконтаэдр|25/25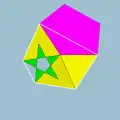
3.3.5/2.3.5		IU40K45601508460{3}+12{5}+12{5/2}
112Плосконосый икосододекододекаэдрСредний шестиугольный гексаконтаэдр|5/33 5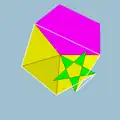
3.3.3.3.5.5/3		IU46K5160180104(20+6){3}+12{5}+12{5/2}
113Большой вывернутый плосконосый икосододекаэдрБольшой вывернутый пятиугольный гексаконтаэдр|5/32 3
3.3.3.3.5/3		IU69K746015092(20+60){3}+12{5/2}
114Вывернутый плосконосый додекододекаэдрМалый вывернутый пятиугольный гексаконтаэдр|5/32 5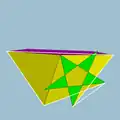
3.5/3.3.3.5		IU60K65601508460{3}+12{5}+12{5/2}
115Большой плосконосый додекоикосододекаэдрБольшой шестиугольный гексаконтаэдр|5/35/23
3.5/3.3.5/2.3.3		IU64K6960180104(20+60){3}+(12+12){5/2}
116Большой плосконосый икосододекаэдрБольшой пятиугольный гексаконтаэдр|25/25/2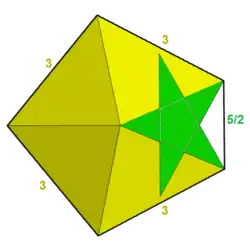
3.3.3.3.5/2		IU57K626015092(20+60){3}+12{5/2}
117Большой вывернутый обратноплосконосый икосододекаэдр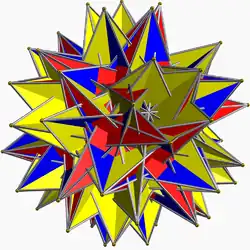Большой пентаграммный гексаконтаэдр|3/25/32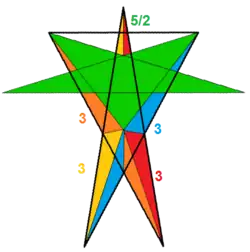
(3.3.3.3.5/2)/2		IU74K796015092(20+60){3}+12{5/2}
118Малый вывернутый обратноплосконосый икосоикосододекаэдрМалый гексаграммный гексаконтаэдр|3/23/25/2
(3.3.3.3.3.5/2)/2		IhU72K7718060112(40+60){3}+12{5/2}
119Большой биромбоикосододекаэдр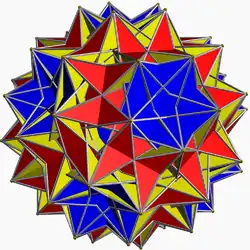Большой биромбоикосододекрон|3/25/335/2
(4.5/3.4.3.4.5/2.4.3/2)/2		IhU75K806024012440{3}+60{4}+24{5/2}

См. также

Литература

  • М. Веннинджер. Модели многогранников. — «Мир», 1974.
    Ошибки в книге Веннинджера. Для многогранника W90 вершинная фигура ошибочно показана как имеющая параллельные рёбра. Для многогранника W106 даны неверные чертежи заготовок, вследствие чего в получаемой модели отсутствуют некоторые видимые части однородного многогранника. У многогранников W113 и W116 перепутаны названия.
  • Magnus Wenninger. Spherical Models. — Cambridge University Press, 1979. — ISBN 0-521-29432-0.

Ссылки

  • Magnus J. Wenninger
  • Для создания изображений для этой статьи использовалось следующее ПО:
    • Stella: Polyhedron Navigator Stella (software) — ПО, способное создать и распечатать nets для всех многогранников, упомянутых в книге Веннинджера;
    • Polyhedra Stellations — аплет Владимира Булатова;
    • Polyhedra Stellations — аплет Владимира Булатова, оформленный в виде пакета для OS X.
  • M. Wenninger, Polyhedron Models, Errata — ошибки, найденные в разных изданиях.
Эта статья взята у (из) Wikipedia. Текст лицензируется по Creative Commons - Attribution - Sharealike. К медиа файлам могут применятся дополнительные условия.