Кодирование Танстелла

Кодирование по Танстеллу — форма энтропийного кодирования, используемая для сжатия данных без потерь.

Кодирование по Танстеллу было предметом докторской диссертации Брайана Паркера Танстелла в 1967 году, когда он работал в Технологическом институте Джорджии. Темой этой диссертации был «Синтез кодов с бесшумным сжатием»^[1].

Является предшественником алгоритма Лемпеля-Зива.

В отличие от кодов переменной длины, одним из которых является кодирование Хаффмана, при кодировании Танстелла сопоставляются исходные символы с фиксированным количеством битов^[2].

Как коды Танстелла, так и коды Лемпеля-Зива представляют слова переменной длины кодами фиксированной длины^[3].

В отличие от кодирования типичных множеств ^{[уточнить]}, кодирование Танстелла анализирует стохастический источник с помощью кодовых слов переменной длины.

Можно показать^[4], что для достаточно большого словаря количество битов на букву источника может быть сколь угодно близко к ${\displaystyle H(U)}$ — энтропии источника.

Алгоритм требует в качестве входных данных входной алфавит ${\displaystyle {\mathcal {U}}}$, а также распределение вероятностей для каждого вводимого слова. Для этого также требуется произвольная константа ${\displaystyle C}$, которая является верхней границей размера словаря, который этот алгоритм будет вычислять. Рассматриваемый словарь, ${\displaystyle D}$, построен как дерево вероятностей, в котором каждое ребро связано с буквой из входного алфавита. Алгоритм выглядит следующим образом:

D: = дерево из ${\displaystyle |{\mathcal {U}}|}$ листьев, по одному на каждую букву в ${\displaystyle {\mathcal {U}}}$.
Пока ${\displaystyle |D|<C}$:
    Преобразуйте наиболее вероятный лист в дерево с ${\displaystyle |{\mathcal {U}}|}$ листьями.

Пусть исходная строка «hello, world». Предположим (несколько нереалистично), что входной алфавит ${\displaystyle {\mathcal {U}}}$ содержит только символы из строки «hello, world», то есть 'h', 'e', 'l', ',', ' ', ' w', 'o', 'r', 'd'. Таким образом, можно вычислить вероятность каждого символа на основе его статистической частоты появления во входной строке. Например, буква L появляется трижды в строке из 12 символов: ее вероятность равна ${\displaystyle 3 \over 12}$.

Нужно инициализировать дерево, начиная с дерева из ${\displaystyle |{\mathcal {U}}|=9}$ листьев. Таким образом, каждое слово напрямую связано с буквой алфавита. 9 слов, которые мы получаем таким образом, могут быть закодированы в выходные данные фиксированного размера ${\displaystyle \lceil \log _{2}(9)\rceil =4}$ бита.

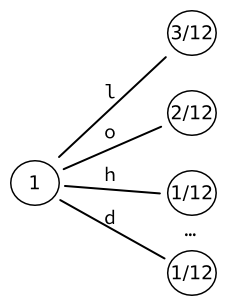
Затем берётся лист с наибольшей вероятностью (здесь, ${\displaystyle w_{1}}$) и преобразуется в еще одно дерево с ${\displaystyle |{\mathcal {U}}|=9}$ листьями, по одному для каждого символа. И нужно повторно вычислить вероятности этих листьев. Например, последовательность из двух букв L встречается один раз. С учётом того, что существует три вхождения букв, следующих за буквой L, результирующая вероятность равна ${\displaystyle {1 \over 3}\cdot {3 \over 12}={1 \over 12}}$.

Каждое из полученных 17 слов может быть закодировано в выходные данные фиксированного размера, состоящие из ${\displaystyle \lceil \log _{2}(17)\rceil =5}$ бит.

Этот процесс можно повторять и дальше, увеличивая количество слов на ${\displaystyle |{\mathcal {U}}|-1=8}$ каждый раз.

Кодирование Танстелла требует, чтобы алгоритм знал до операции непосредственно кодирования, каково распределение вероятностей для каждой буквы алфавита. Эта проблема является общей с кодированием Хаффмана.

Его требование вывода блока фиксированной длины делает результат меньшим, чем у Лемпеля-Зива, который имеет аналогичный дизайн на основе словаря, но с выводом блока переменного размера.^{[прояснить]}