Контактное число
Контактное число (иногда число Ньютона[1][2], в химии соответствует координационному числу[2]) — максимальное количество n-мерных шаров единичного радиуса, которые могут одновременно касаться одного такого же шара в n-мерном евклидовом пространстве (предполагается, что шары не проникают друг в друга, то есть объём пересечения любых двух шаров равен нулю).
Следует отличать контактное число от контактного числа на решётке[3] — аналогичного параметра для плотнейшей регулярной упаковки шаров. Вычисление контактного числа в общем случае до сих пор является нерешённой математической задачей.
История
В одномерном случае не более двух отрезков единичной длины могут касаться такого же отрезка:

В двумерном случае можно интерпретировать задачу как нахождение максимального числа монет, касающихся центральной. Из рисунка видно, что разместить можно до 6 монет:
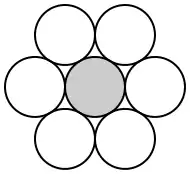
Это значит, что . С другой стороны, каждая касающаяся окружность отсекает на центральной окружности дугу в 60°, и эти дуги не пересекаются, значит . Видно, что в данном случае оценки сверху и снизу совпали и .
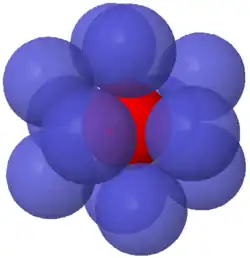
В трёхмерном случае речь идет о шарах. Здесь также легко построить пример с 12 шарами, касающимися центрального — они расположены в вершинах икосаэдра — поэтому . Данная нижняя оценка была известна ещё Ньютону.
Это расположение неплотное, между шарами будут довольно заметные зазоры. Оценка сверху стала причиной известного спора между Ньютоном и Д. Грегори в 1694 году. Ньютон утверждал, что , а Грегори возражал, что может быть можно расположить и 13 шаров. Он провёл вычисления и выяснил, что площадь центрального шара более чем в 14 раз больше площади проекции каждого из касающихся шаров, так что . Если позволить менять радиусы шаров на 2 %, то оказывается возможным прислонить до 14 шаров.
Лишь в 1953 году в статье Шютте и ван дер Вардена[4] была окончательно установлена правота Ньютона, несмотря на отсутствие у того строгого доказательства.
В четырёхмерном случае представить себе шары достаточно сложно. Размещение 24 четырёхмерных сфер вокруг центральной было известно давно, оно столь же регулярное, как и в двумерном случае, и решает одновременно и задачу о контактном числе на решётке. Это то же размещение, что у целых единичных кватернионов.
В явном виде это расположение было указано в 1900 году Госсетом[5]. Ещё раньше оно было найдено (в эквивалентной задаче) в 1872 году российскими математиками Коркиным и Золотарёвым[6][7]. Это расположение дало оценку снизу .
Попытки оценить это число сверху привели к развитию тонких методов теории функций, но не давали точного результата. Сначала удалось доказать, что , потом удалось снизить верхнюю границу до . И наконец в 2003 году российскому математику Олегу Мусину удалось доказать, что [8].
В размерностях 8 и 24 точная оценка была получена в 1970-е годы[9][10]. Доказательство основано на равенстве контактного числа и контактного числа на решётке в этих размерностях: решётки E8 (для размерности 8) и решётки Лича (для размерности 24).
В 2025 году ИИ AlphaEvolve от компании Google DeepMind улучшил нижнюю границу контактного числа в 11-мерном пространстве с 592 до 593[11].
Известные значения и оценки
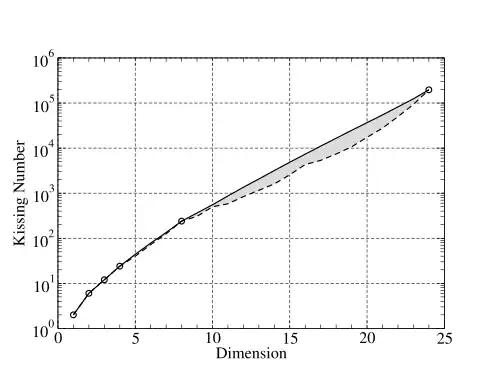
В настоящее время точные значения контактных чисел известны только для , а также для и . Для других размерностей известны только верхние и нижние оценки, но не точные значения[12].
| Размерность | Нижняя граница | Верхняя граница |
|---|---|---|
| 1 | 2 | |
| 2 | 6 | |
| 3 | 12 | |
| 4 | 24[8] | |
| 5 | 40 | 44[13] |
| 6 | 72 | 78[13] |
| 7 | 126 | 134[13] |
| 8 | 240 | |
| 9 | 306 | 364[13] |
| 10 | 510[14] | 554 |
| 11 | 593[11] | 870 |
| 12 | 840 | 1 357 |
| 13 | 1 154[15] | 2 069 |
| 14 | 1 932[14] | 3 183 |
| 15 | 2 564 | 4 866 |
| 16 | 4 320 | 7 355 |
| 17 | 5 346 | 11 072 |
| 18 | 7 398 | 16 572[13] |
| 19 | 10 688 | 24 812[13] |
| 20 | 17 400 | 36 764[13] |
| 21 | 27 720 | 54 584[13] |
| 22 | 49 896 | 82 340 |
| 23 | 93 150 | 124 416 |
| 24 | 196 560 | |
Приложения
Задача имеет практическое применение в теории кодирования. В 1948 году Клод Шеннон опубликовал работу по теории информации, показывающую возможность передачи данных без ошибок в зашумленных каналах связи используя координаты упаковки единичных сфер в n-мерном пространстве. См. также Расстояние Хэмминга.
См. также
Примечания
- ↑ Яглом, И. М. Проблема тринадцати шаров. — Киев: Вища школа, 1975. — 84 с. Архивировано 28 июня 2020 года.
- 1 2 Дж. Конвей, Н. Слоэн. Упаковки шаров, решётки и группы. — М.: Мир, 1990. — Т. 1. — 415 с. — ISBN 5-03-002368-2. Архивировано 6 октября 2014 года. Архивированная копия. Дата обращения: 29 мая 2011. Архивировано 6 октября 2014 года.
- ↑ Контактные числа на решётках: последовательность A001116 в OEIS
- ↑ Schütte, K. and van der Waerden, B. L. Das Problem der dreizehn Kugeln (неопр.) // Math. Ann.. — 1953. — Т. 125, № 1. — С. 325—334. — doi:10.1007/BF01343127.
- ↑ Gosset, Thorold. On the regular and semi-regular figures in space of n dimensions (англ.) // Messenger of Mathematics : journal. — 1900. — Vol. 29. — P. 43—48.
- ↑ Korkine A., Zolotareff G. Sur les formes quadratiques positives quaternaires (неопр.) // Math. Ann.. — 1872. — Т. 5, № 4. — С. 581—583. — doi:10.1007/BF01442912. Рус. пер.: Золотарёв Е. И. Полн. собр. соч. — Л.: Изд-во АН СССР, 1931. — С. 66—68.
- ↑ Н. Н. Андреев, В. А. Юдин. Арфиметический минимум квадратичной формы и сферические коды // Математическое просвещение. — 1998. — № 2. — С. 133—140. Архивировано 3 марта 2022 года.
- 1 2 Мусин О. Р. Проблема двадцати пяти сфер // Успехи математических наук. — Российская академия наук, 2003. — Т. 58, № 4(352). — С. 153—154.
- ↑ Левенштейн В. И. О границах для упаковок в n-мерном евклидовом пространстве // ДАН СССР. — 1979. — Т. 245. — С. 1299—1303.
- ↑ A. M. Odlyzko, N. J. A. Sloane. New bounds on the number of unit spheres that can touch a unit sphere in n dimensions (англ.) // J. Combin. Theory Ser. A : journal. — 1979. — Vol. 26. — P. 210—214. — doi:10.1016/0097-3165(79)90074-8.
- 1 2 Meet AlphaEvolve, the Google AI that writes its own code—and just saved millions in computing costs
- ↑ Mittelmann, Hans D.; Vallentin, Frank (2010). High accuracy semidefinite programming bounds for kissing numbers. Experimental Mathematics. 19 (2): 174–178. arXiv:0902.1105. Bibcode:2009arXiv0902.1105M. doi:10.1080/10586458.2010.10129070. S2CID 218279.
- 1 2 3 4 5 6 7 8 Hans D. Mittelmann and Frank Vallentin. [http://arxiv.org/abs/0902.1105 High-Accuracy Semidefinite Programming Bounds for Kissing Numbers] // Experimental Mathematics. — 2010. — Т. 19, № 2. — С. 174—178. Архивировано 11 августа 2020 года.
- 1 2 Mikhail Ganzhinov. Highly symmetric lines // arXiv:2207.08266 [math]. — 2022-07-17. Архивировано 30 марта 2023 года.
- ↑ В. А. Зиновьев, Т. Эриксон. Новые нижние оценки на контактное число для небольших размерностей // Пробл. передачи информ.. — 1999. — Т. 35, № 4. — С. 3—11.
Ссылки
- Контактное число шаров и сферические коды. Математические этюды.
- Шарыгин, Г. И. Контактные числа и проблема тринадцати шаров // Математика. — Издательский дом «Первое сентября», 2007. — № 9 (623).
- Шарыгин, Г. И. Контактные числа и проблема тринадцати шаров // Потенциал. — 2009. — № 6.
- Арестов В. В., Бабенко А. Г. О схеме Дельсарта оценки контактных чисел // Труды Мат. ин-та им. В. А. Стеклова РАН. — 1997. — Т. 219. — С. 44—73.