Логарифмически выпуклое множество

Выпуклая оболочка логарифмического образа несвязного множества

Логарифми́чески вы́пуклое мно́жество (англ. logarithmically convex set) — понятие вещественного и комплексного анализа, разделов математики, множество комплексного пространства, логарифмический образ которого выпукл в вещественном пространстве^[1].

Определение логарифмически выпуклого множества

Логарифмический образ $M^{*}$ (англ. logarithmically image $\log M$ ) множества $M\subset \mathbb {C} ^{n}$ — множество

M^{*}=\lambda (M_{0})

,

где^[1]:

\lambda \colon \{z\in \mathbb {C} ^{n}\colon z_{1}z_{2}\dots z_{n}\neq 0\}\to \mathbb {R} ^{n}\colon z\to \lambda (z)=(\operatorname {ln} |z_{1}|,\,\operatorname {ln} |z_{2}|,\,\dots ,\,\operatorname {ln} |z_{n}|),

M_{0}=\{z\in M\colon z_{1}z_{2}\dots z_{n}\neq 0\}.

Другими словами, это следующее множество^[2]:

M^{*}=\{\xi \colon \xi \in \mathbb {R} ^{n},\,(e^{\xi _{1}},\,e^{\xi _{2}},\,\dots ,\,e^{\xi _{n}})=(|z_{1}|,\,|z_{2}|,\,\dots ,\,|z_{n}|),\,(z_{1},\,z_{2},\,\dots ,\,z_{n})\in M\}.

Логарифмически выпуклое множество (англ. logarithmically convex set) — множество $M\subset \mathbb {C} ^{n}$ с выпуклым логарифмическим образом $M^{*}\subset \mathbb {R} ^{n}$ ^[1]^[3].

В терминах определения понятия «выпуклость» это определение перепишется следующим образом^[4]^[5]:

логарифмически выпуклое множество — множество

M\subset \mathbb {C} ^{n}

, которое вместе с двумя произвольными своими точками

z'

и

z''

содержит также и любые точки

z

, для которых

\operatorname {ln} |z|=t\operatorname {ln} |z'|+(1-t)\operatorname {ln} |z''|,\quad

t\in (0,\,1).

Чтобы избежать не совсем удобных логарифмов, поскольку для $z_{k}=0$ получается $\operatorname {ln} |z_{k}|=-\infty$ при некоторых $k$ , перепишем определение в следующем виде^[3]:

логарифмически выпуклое множество — множество

M\subset \mathbb {C} ^{n}

, которое вместе с двумя произвольными своими точками

z'

и

z''

содержит также и любые точки

z

|z|=|z'|^{t}|z''|^{1-t},\quad

t\in (0,\,1),

то есть

|z_{k}|=|z'_{k}|^{t}|z''_{k}|^{1-t},\quad

k=1,\,2,\,\dots ,\,n.

Логарифмически выпуклая оболочка множества (англ. logarithmically convex hull of set) ${\hat {M}}_{L}$ — пересечение всех логарифмически выпуклых множеств, содержащих исходное множество $M$ , другими словами, наименьшее логарифмически выпуклое множество, содержащее исходное множество $M$ ^[1]^[6]^[3].

Например, для множества

M=\{z\in \mathbb {C} ^{2};\,\max(|z_{1}|,\,|z_{2}|)<1,\,\min(|z_{1}|,\,|z_{2}|)<\epsilon \}

логарифмически выпуклая оболочка следующая^[6]:

{\hat {M}}_{L}=\left\{z\in \mathbb {C} ^{2};\,\max \left(|z_{1}|,\,|z_{2}|,\,{\frac {|z_{1}z_{2}|}{\epsilon }}\right)<1\right\}.

Примеры

Пример 1

Этот пример взят из книги на русском языке, написанной русским математиком^[1].

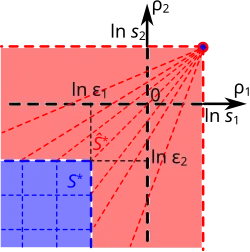
Рассмотрим некоторое множество $M\subset \mathbb {C} ^{2}$ с диаграммой Рейнхарта $\alpha (M)$ , показанной на рисунке ниже слева. Это множество не относится к логарифмически выпуклым. Логарифмический образ $\lambda (M_{0})$ этого множества показана на рисунке ниже справа^[1].

Диаграмма Рейнхарта и логарифмический образ в C×C
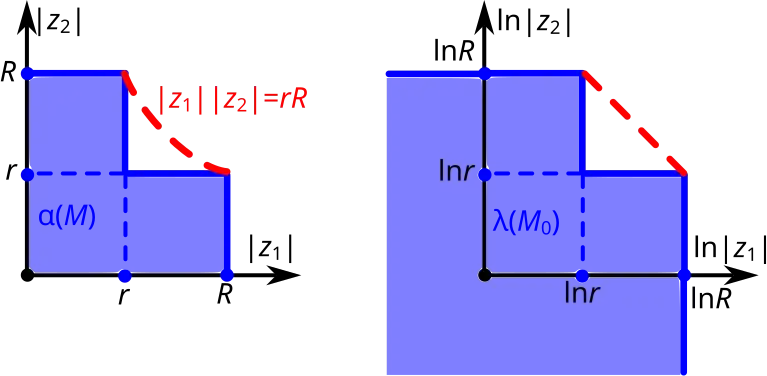$Диаграмма Рейнхарта логарифмически выпуклой оболочки α ( M ^ L ) {\displaystyle \alpha ({\hat {M}}_{L})} некоторого множества M {\displaystyle M} в C 2 {\displaystyle \mathbb {C} ^{2}} и выпуклая оболочка его логарифмического образа λ ( M 0 ) {\displaystyle \lambda (M_{0})}$
Диаграмма Рейнхарта логарифмически выпуклой оболочки $\alpha ({\hat {M}}_{L})$ некоторого множества $M$ в $\mathbb {C} ^{2}$ и выпуклая оболочка его логарифмического образа $\lambda (M_{0})$

Прообраз выпуклой оболочки логарифмического образа $\lambda (M_{0})$ есть логарифмически выпуклая оболочка ${\hat {M}}_{L}$ множества $M$ . Диаграммы Рейнхарта оболочки $\alpha ({\hat {M}}_{L})$ и исходного множества $\alpha (M)$ отличаются только сегментом, граница которого показан пунктиром на рисунке. Этот сегмент получен как прообраз треугольника, дополняющего логарифмический образ $\lambda (M_{0})$ до выпуклости. Гипотенуза этого треугольника есть отрезок прямой

\operatorname {ln} |z_{2}|=\operatorname {ln} |r|+\operatorname {ln} |R|-\operatorname {ln} |z_{1}|

,

поэтому сегмент выпуклости, добавленный к диаграмме Рейнхарта $\alpha (M)$ , ограничен частью следующей гиперболы^[1]:

|z_{2}||z_{1}|=|r||R|

.

Пример 2

Этот и следующий примеры взяты из книги на английском языке, написанной голландскими математиками^[3].

Рассмотрим объединение $S$ двух следующих прямоугольников (см. рис. внизу слева)^[3]:

S_{1}=\left\{(r_{1},\,r_{2})\in \mathbb {R} _{+}^{2}\colon r_{1}<2,\,r_{1}<{\frac {1}{2}}\right\},

S_{2}=\left\{(r_{1},\,r_{2})\in \mathbb {R} _{+}^{2}\colon r_{1}<{\frac {1}{2}},\,r_{1}<2\right\}.

Вещественная область и логарифмический образ в R×R
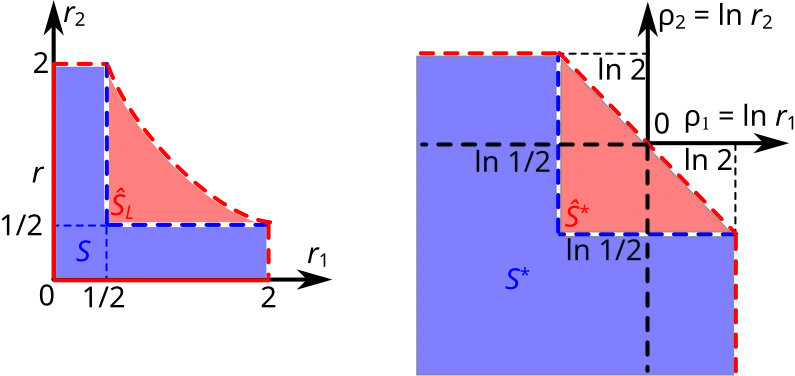$Логарифмически выпуклая оболочка S ^ L {\displaystyle {\hat {S}}_{L}} некоторого множества S {\displaystyle S} в R + 2 {\displaystyle \mathbb {R} _{+}^{2}} и выпуклая оболочка S ^ ∗ {\displaystyle {\hat {S}}^{*}} его логарифмического образа S ∗ {\displaystyle S^{*}}$
Логарифмически выпуклая оболочка ${\hat {S}}_{L}$ некоторого множества $S$ в $\mathbb {R} _{+}^{2}$ и выпуклая оболочка ${\hat {S}}^{*}$ его логарифмического образа $S^{*}$

Логарифмический образ $S^{*}$ множества $S$ есть объединение следующих квадрантов — логарифмических образов данных прямоугольников (см. рис. вверху справа):

S_{1}^{*}=\left\{(\rho _{1},\,\rho _{2})\in \mathbb {R} ^{2}\colon \rho _{1}<\operatorname {ln} 2,\,\rho _{2}<\operatorname {ln} {\frac {1}{2}}\right\},

S_{2}^{*}=\left\{(\rho _{1},\,\rho _{2})\in \mathbb {R} ^{2}\colon \rho _{1}<\operatorname {ln} {\frac {1}{2}},\,\rho _{2}<\operatorname {ln} 2\right\}.

которые содержат точки с координатами $-\infty$ ^[3].

Выпуклая оболочка ${\hat {S}}^{*}$ множества $S^{*}$ образована точками $(\rho _{1},\,\rho _{2})$ , которые удовлетворяют следующим условиям (см. рис. вверху справа)^[3]:

\rho _{1}<\operatorname {ln} 2,\quad \rho _{2}<\operatorname {ln} 2,\quad \rho _{1}+\rho _{2}<0.

Логарифмически выпуклая оболочка ${\hat {S}}_{L}$ множества $S$ образована точками $(r_{1},\,r_{2})=(e^{\rho _{1}},\,e^{\rho _{2}})$ , где $(\rho _{1},\,\rho _{2})\in {\hat {S}}_{L}$ , то есть точками $r_{1},\,r_{2}\geqslant 0$ , удовлетворяющим следующим условиям (см. рис. вверху слева)^[3]:

r_{1}<2,\quad r_{2}<2,\quad r_{1}r_{2}=e^{\rho _{1}+\rho _{2}}<1.

Пример 3

Рассмотрим несвязное множество $S$ , представляющее собой объединение изолированной точки

s=(s_{1},\,s_{2},\,\dots ,\,s_{n})>0

и следующей окрестности нуля в пространстве $\mathbb {R} _{+}^{n}$ ^[3]:

0\leqslant r_{j}<\epsilon _{j}<s_{j},\quad j=1,\,2,\,\dots ,\,n.

Тогда логарифмически выпуклая оболочка ${\hat {S}}_{L}$ множества $S$ содержит множество точек

0\leqslant r_{j}<s_{j},\quad j=1,\,2,\,\dots ,\,n,

логарифмический образ которого показан на рисунке справа для двумерного случая^[3].

Примечания

1 2 3 4 5 6 7 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 7. Степенные ряды, с. 44.
↑ Хёрмандер, Ларс Введение в теорию функций нескольких комплексных переменных, 1968, 2.4. Степенные ряды и области Рейихарта, с. 56, 59.
1 2 3 4 5 6 7 8 9 10 Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 2.2 Auxiliary results on convexity, p. 29.
↑ Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 33. Псевдовыпуклые области, с. 44.
↑ Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 2.2 Auxiliary results on convexity, p. 28.
1 2 Хёрмандер, Ларс Введение в теорию функций нескольких комплексных переменных, 1968, 2.4. Степенные ряды и области Рейихарта, с. 59.

Источники

Хёрмандер, Ларс. Введение в теорию функций нескольких комплексных переменных / Пер. с англ. Е. М. Чирки, под ред. Б. В. Шабата. М.: «Мир», 1968. 279 с.
Шабат Б. В. Введение в комплексный анализ, ч. II, изд. 2-е, перераб. и доп. М.: «Наука», 1976. 400 с.: ил.
Jaap Korevaar, Jan Wiegerinck. Several Complex Variables. Amsterdam: University of Amsterdam, November 18, 2011. 260 p.

[_57ba80876aac69b7-1] 1 2 3 4 5 6 7 Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 7. Степенные ряды, с. 44.

[_5db1585a4f2e1686-2] Хёрмандер, Ларс Введение в теорию функций нескольких комплексных переменных, 1968, 2.4. Степенные ряды и области Рейихарта, с. 56, 59.

[_485c38ac29c71899-3] 1 2 3 4 5 6 7 8 9 10 Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 2.2 Auxiliary results on convexity, p. 29.

[_2e35c2b8b9f74ed3-4] Шабат Б. В. Введение в комплексный анализ, ч. II, 1976, 33. Псевдовыпуклые области, с. 44.

[_3e0d55ac23791112-5] Jaap Korevaar, Jan Wiegerinck Several Complex Variables, 2011, 2.2 Auxiliary results on convexity, p. 28.

[_2a132782a4e724ad-6] 1 2 Хёрмандер, Ларс Введение в теорию функций нескольких комплексных переменных, 1968, 2.4. Степенные ряды и области Рейихарта, с. 59.

[1]

[2]

[3]

[4]

[5]

[6]