Мутация (теория узлов)

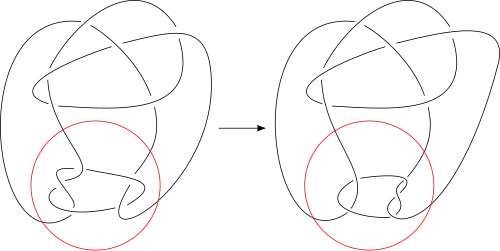
В теории узлов мутация — это специальный вид преобразования узлов. Мутация выбирает маленькую часть узла и либо отражает, либо поворачивает её, вследствие чего получается некий новый (возможно исходный) узел, который называется мутантом исходного.

Пусть K — узел, заданный в виде диаграммы. Пусть D — диск в плоскости диаграммы, границы которого пересекают K ровно четыре раза. Можно считать (в случае необходимости используем изотопию), что диск геометрически круглый и четыре точки пересечения расположены на равном расстоянии. Часть узла внутри диска называется диаграммой тэнгла. Имеется два отражения, которые меняют местами пары концов нитей на диаграмме этого тэнгла. Кроме того, имеются также вращения. Мутация заменяет исходный тэнгл на тэнгл, полученный любой из этих операций. В результате получается узел, который называется мутацией узла K^[1].

Пару узлов, связанных мутацией, называют узлами-мутантами или просто мутантами. Здесь слово «мутант» используется в значении «результат мутации» и всегда имеет отношение сразу к двум узлам. Пример использования: Узел ${\displaystyle K}$ мутант узла ${\displaystyle Q}$, узлы ${\displaystyle K}$ и ${\displaystyle Q}$ мутанты (по отношению друг ко другу).

• Если один мутант тривиален, то и другой тривиален. Иными словами, из тривиального узла мутацией можно получить только тривиальный узел, или, что равносильно, тривиальный узел является изолированной вершиной в гордиевом графе мутации.^[2]
• Многие классические инварианты у мутантов совпадают, поэтому нередко задача различения двух узлов, связанных мутацией, оказывается достаточно сложной. Так, например, узлы-мутанты имеют одинаковый гиперболический объём (результат Рубемана), Многочлен Александера, сигнатуру, гомологии разветвленных накрытий, n-раскрашиваемость и многочлен HOMFLY.
• Однако группа узла и род могут различить мутантов.

• Пара узлов, Конвея и Киношиты-Терасака, являются мутантами друг друга, но имеют различный род, равный 3 и 2 соответственно.

• Adams C. C. The Knot Book. An Elementary Introduction to the Mathematical Theory of Knots (англ.). — New York: American Mathematical Society, 2004. — 307 p. — ISBN 978-0821836781.

• Cromwell P. R. Knots and Links (англ.). — Cambridge: Cambridge University Press, 2004. — 328 p. — ISBN 9780511809767.

• Livingston C. Knot Theory (англ.). — The Mathematical Association of America, 1996. — Vol. 24. — 258 p. — (The Carus Mathematical Monographs). — ISBN 978-0883850275.

• Morton H. R. Mutant knots (англ.) // New ideas in low dimensional topology. — 2015. — P. 379—412. — doi:10.1142/9789814630627_0010.