Узел Конвея

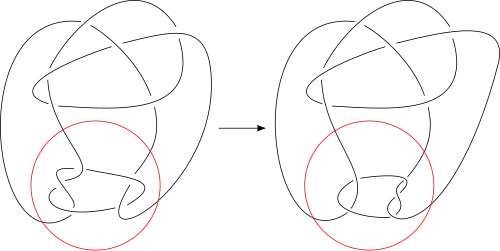
Узел Конвея — определённый узел, примечательный тем, что некоторые вопросы теории узлов применительно к нему оказываются особенно сложными. Назван в честь британского математика Джона Хортона Конвея, который описал этот узел в 1970 году. В таблицах Дейла Рольфсена и в атласе узлов он имеет номер K11n34.

Минимальное число пересечений узел Конвея равно 11.

Группа кос для узла Конвея^[1]:

${\displaystyle \sigma _{2}^{3}\sigma _{1}\sigma _{3}^{-1}\sigma _{2}^{-2}\sigma _{1}\sigma _{2}^{-1}\sigma _{1}\sigma _{3}^{-1}}$.

Полином Джонса для узла Конвея равен 1:

${\displaystyle t^{-4}(-1+2t-2t^{2}+2t^{3}+t^{6}-2t^{7}+2t^{8}-2t^{9}+t^{10})}$.

Гиперболический объём узла Конвея равен 11,2191.

• Узел Конвея изображен на воротах Института Исаака Ньютона в Кембриджском университете^[5].
• Узел Конвея представлен среди экспонатов передвижной художественной инсталляции Mathemalchemy^[6].

• Узел Конвея в Атласе Узлов