Последовательность Баркера
После́довательность Ба́ркера — это числовая последовательность , где каждый элемент равен +1 или -1, причём
для всех .
Известные последовательности Баркера
С точностью до реверсирования порядка и смены знаков каждого из элементов, известны только девять последовательностей Баркера, самая длинная из которых имеет длину 13:[1]
| Длина | Последовательности | |
|---|---|---|
| 2 | +1 −1 | +1 +1 |
| 3 | +1 +1 −1 | |
| 4 | +1 −1 +1 +1 | +1 −1 −1 −1 |
| 5 | +1 +1 +1 −1 +1 | |
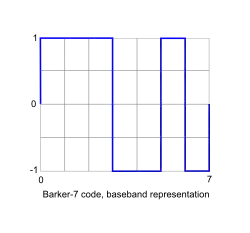
| 7 | +1 +1 +1 −1 −1 +1 −1 | |
| 11 | +1 +1 +1 −1 −1 −1 +1 −1 −1 +1 −1 | |
| 13 | +1 +1 +1 +1 +1 −1 −1 +1 +1 −1 +1 −1 +1 | |
Свойства
- Последовательности Баркера имеют минимальный уровень боковых лепестков автокорреляционной функции .
Приложения
- Последовательность Баркера с 11 членами используется в цифровых системах передачи данных.
- Быстрая синхронизация приемника с передатчиком определяет возможность её использования в технологии DSSS.
См. также
Примечания
- ↑ Borwein, Peter; Mossinghoff, Michael J. Barker sequences and flat polynomials // Number Theory and Polynomials (англ.) / James McKee; Chris Smyth. — Cambridge University Press, 2008. — Vol. 352. — P. 71—88. — (LMS Lecture Notes). — ISBN 978-0-521-71467-9.
Ссылки
- Weisstein, Eric W. Barker Code (англ.) на сайте Wolfram MathWorld.