Теорема Вейерштрасса о рядах голоморфных функций

1. Непрерывность суммы ряда. Так как ряд

${\displaystyle f(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots =\sum \limits _{k=1}^{\infty }f_{k}(z)}$

сходится равномерно, то, по теореме о непрерывности суммы ряда, его сумма ${\displaystyle f(z)}$ — непрерывная функция в любой замкнутой области ${\displaystyle {\bar {D'}}\subset D}$, следовательно, и во всей области ${\displaystyle D}$. Осталось доказать, что в любой точке ${\displaystyle z_{0}}$ области ${\displaystyle D}$ у функции ${\displaystyle f(z)}$ есть конечная производная.

2. Замкнутый контур. Построим вокруг произвольной точки ${\displaystyle z_{0}\in D}$ замкнутый кусочно-гладкий контур ${\displaystyle C}$ такой, что сам контур и его внутренность лежат в области ${\displaystyle D}$. На этом контуре ${\displaystyle C}$ данный ряд сходится равномерно по условию теоремы. Пусть ${\displaystyle w}$ — любая точка на контуре ${\displaystyle C}$, а ${\displaystyle z}$ — любая точка внутри контура ${\displaystyle C}$. Тогда разделим все члены ряда на разность ${\displaystyle w-z}$, получим ряд

${\displaystyle {\frac {f(w)}{w-z}}={\frac {f_{1}(w)}{w-z}}+{\frac {f_{2}(w)}{w-z}}+\cdots +{\frac {f_{k}(w)}{w-z}}+\cdots }$,

который равномерно сходится для любых точек ${\displaystyle z\in C}$. Такой ряд, согласно теореме об интегрировании равномерно сходящегося ряда, почленно интегрируется вдоль замкнутой кривой ${\displaystyle C}$.

3. Интегрирование вдоль контура. Проинтегрируем ряд вдоль замкнутой кривой ${\displaystyle C}$, поделив все члены ряда на ${\displaystyle 2\pi i}$:

${\displaystyle {\frac {1}{2\pi i}}\int \limits _{C}{\frac {f(w)dw}{w-z}}={\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{1}(w)dw}{w-z}}+}$

${\displaystyle {}+{\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{2}(w)dw}{w-z}}+\cdots +{\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{k}(w)dw}{w-z}}+\cdots }$,

и поскольку функции ${\displaystyle f_{k}(z)}$ аналитические всюду внутри контура ${\displaystyle C}$ и на самом контуре по условию теоремы, то, по интегральной формуле Коши, перепишем последний ряд в следующем виде:

${\displaystyle {\frac {1}{2\pi i}}\int \limits _{C}{\frac {f(w)dw}{w-z}}=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots }$,

то есть снова в виде интегральной формуле Коши

${\displaystyle f(z)={\frac {1}{2\pi i}}\int \limits _{C}{\frac {f(w)dw}{w-z}}}$.

4. Конечная производная. Поскольку последняя интегральной формуле Коши для функции ${\displaystyle f(z)}$ верна для всех внутренних точек ${\displaystyle z}$ контура ${\displaystyle C}$, то, в силу соответствующей теоремы, во всех этих точках ${\displaystyle f(z)}$ имеет конечную производную

${\displaystyle f'(z)={\frac {1}{2\pi i}}\int \limits _{C}{\frac {f(w)dw}{(w-z)^{2}}}}$,

в частности, у функции ${\displaystyle f(z)}$ есть конечная производная в точке ${\displaystyle z=z_{0}}$. Но ${\displaystyle z_{0}}$ — это, по определению, любая точка области ${\displaystyle D}$, следовательно, в области ${\displaystyle D}$ функция ${\displaystyle f(z)}$ аналитическая, что и требовалось доказать.

1. Непрерывность суммы ряда. Так как ряд

${\displaystyle f(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots =\sum \limits _{k=1}^{\infty }f_{k}(z)}$

сходится равномерно, то, по теореме о непрерывности суммы ряда, его сумма ${\displaystyle f(z)}$ — непрерывная функция в любой замкнутой области ${\displaystyle {\bar {D'}}\subset D}$, следовательно, и во всей области ${\displaystyle D}$.

2. Замкнутый контур. Построим вокруг произвольной точки ${\displaystyle z_{0}\in D}$ замкнутый кусочно-гладкий контур ${\displaystyle C}$ такой, что сам контур и его внутренность лежат в области ${\displaystyle D}$. На этом контуре ${\displaystyle C}$ данный ряд сходится равномерно по условию теоремы. Следовательно, он интегрируется почленно вдоль кривой ${\displaystyle C}$:

${\displaystyle \int \limits _{C}f(w)dw=\int \limits _{C}f_{1}(w)dw+}$

${\displaystyle {}+\int \limits _{C}f_{2}(w)dw+\cdots +\int \limits _{C}f_{k}(w)dw+\cdots }$,

а поскольку все функции ${\displaystyle f_{k}(z)}$ аналитические внутри и на контуре ${\displaystyle C}$, то по интегральной теореме Коши

${\displaystyle \int \limits _{C}f_{k}(w)dw=0,\quad k=1,\,2,\,3,\,\dots }$,

откуда

${\displaystyle \int \limits _{C}f(w)dw=0}$.

3. Теорема Мореры. Получили, что сумма ряда из условия теоремы — это непрерывная функция ${\displaystyle f(z)}$ в области ${\displaystyle D}$, причём интеграл ${\displaystyle \int \limits _{C}f(w)dw=0}$ берётся вдоль любого замкнутого контура ${\displaystyle C}$ из некоторой окрестности точки ${\displaystyle z_{0}}$. Тогда, по теореме Мореры, функция ${\displaystyle f(z)}$ в указанной выше окрестности точки ${\displaystyle z_{0}}$ аналитическая. Но ${\displaystyle z_{0}}$ — это, по определению, любая точка области ${\displaystyle D}$, следовательно, в области ${\displaystyle D}$ функция ${\displaystyle f(z)}$ аналитическая, что и требовалось доказать.

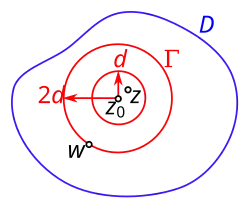
1. Окрестность точки. Рассмотрим любую точку ${\displaystyle z_{0}}$ области ${\displaystyle D}$, ${\displaystyle z_{0}\in D}$. Построим окружность ${\displaystyle \Gamma \colon |z-z_{0}|=2d}$ с центром в точке ${\displaystyle z_{0}}$ и такого маленького радиуса ${\displaystyle 2d>0}$, чтобы она и весь замкнутый круг ${\displaystyle |z-z_{0}|\leqslant 2d}$ принадлежали области ${\displaystyle D}$. Осталось доказать, что сумма ряда ${\displaystyle f(z)}$ из условия теоремы — это аналитическая функция в ${\displaystyle d}$-окрестности ${\displaystyle |z-z_{0}|<d}$ точки ${\displaystyle z_{0}}$.

2. Равномерная сходимость. Возьмём две произвольные точки: ${\displaystyle w}$ на окружности ${\displaystyle \Gamma }$, ${\displaystyle w\in \Gamma }$, и ${\displaystyle z}$ в ${\displaystyle d}$-окрестности ${\displaystyle |z-z_{0}|<d}$. Преобразуем ряд

${\displaystyle f(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots }$

из условия теоремы, заменив ${\displaystyle z}$ на ${\displaystyle w}$ и умножив на ${\displaystyle {\frac {1}{2\pi i(w-z)}}}$, получим:

${\displaystyle {\frac {1}{2\pi i}}{\frac {f(w)}{w-z}}={\frac {1}{2\pi i}}{\frac {f_{1}(w)}{w-z}}+{\frac {1}{2\pi i}}{\frac {f_{2}(w)}{w-z}}+\cdots +{\frac {1}{2\pi i}}{\frac {f_{k}(w)}{w-z}}+\cdots }$,

а поскольку исходный ряд из условия теоремы равномерно сходится на окружности ${\displaystyle \Gamma }$, причём

${\displaystyle \left|{\frac {1}{2\pi i(w-z)}}\right|<{\frac {1}{2\pi d}}}$,

то новый ряд также равномерно сходится на окружности ${\displaystyle \Gamma }$ и его можно почленно интегрировать. По интегральной формуле Коши интеграл от каждого члена нового ряда равен ${\displaystyle f_{k}(z)}$, и получаем:

${\displaystyle {\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {f(w)dw}{w-z}}=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots =f(z)}$,

то есть в ${\displaystyle d}$-окрестности точки ${\displaystyle z_{0}}$ сумма ряда ${\displaystyle f(z)}$ из условия теоремы представлена интегралом типа Коши:

${\displaystyle f(z)={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {f(w)dw}{w-z}}}$,

а это означает, что ${\displaystyle f(z)}$ — аналитическая функция в точке ${\displaystyle z_{0}}$. Но ${\displaystyle z_{0}\in D}$ — произвольная точка, поэтому ${\displaystyle f(z)}$ — аналитическая функция в области ${\displaystyle D}$.

Пусть ${\displaystyle S_{N}(z)}$ — частичная сумма исходного ряда

${\displaystyle f(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots =\sum \limits _{k=1}^{\infty }f_{k}(z)}$,

то есть

${\displaystyle S_{N}(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{N}(z)=\sum \limits _{k=1}^{N}f_{k}(z)}$.

1. Окрестность точки. Рассмотрим любую точку ${\displaystyle z_{0}}$ области ${\displaystyle D}$, ${\displaystyle z_{0}\in D}$. Построим окружность ${\displaystyle \Gamma \colon |z-z_{0}|=2d}$ с центром в точке ${\displaystyle z_{0}}$ и такого маленького радиуса ${\displaystyle 2d>0}$, чтобы она и весь замкнутый круг ${\displaystyle |z-z_{0}|\leqslant 2d}$ принадлежали области ${\displaystyle D}$. Осталось доказать, что сумма предел последовательности ${\displaystyle S_{N}(z)}$ — это аналитическая функция в ${\displaystyle d}$-окрестности ${\displaystyle |z-z_{0}|<d}$ точки ${\displaystyle z_{0}}$.

2. Равномерная сходимость. Поскольку для любого ${\displaystyle N\in \mathbb {N} }$ новая функция ${\displaystyle S_{N}(z)}$ аналитична в области ${\displaystyle D}$, то по интегральной формуле Коши для любого ${\displaystyle z\in \Gamma }$

${\displaystyle S_{N}(z)={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {S_{N}(w)}{w-z}}dw}$.

Так как, по условию теоремы, исходный ряд равномерно сходится в любой замкнутой подобласти области ${\displaystyle D}$, в сами функции ${\displaystyle f_{k}(z)}$ непрерывны в области ${\displaystyle D}$, то, по теореме о непрерывности, частичная сумма ряда ${\displaystyle S_{N}(z)}$ также непрерывна в области ${\displaystyle D}$.

Далее, вследствие равномерной сходимости исходного ряда в замкнутом круге ${\displaystyle |z-z_{0}|\leqslant 2d}$ имеем, что для любого числа ${\displaystyle \epsilon >0}$ найдётся такое ${\displaystyle N(\epsilon )}$, что для любого ${\displaystyle N\leqslant N(\epsilon )}$ верно неравенство

${\displaystyle \sup _{w\in \Gamma }|S_{N}(w)-f(w)|<\epsilon }$.

Отсюда для произвольной точки ${\displaystyle z}$ из ${\displaystyle d}$-окрестности и натурального числа ${\displaystyle N\geqslant N(\epsilon )}$ имеем:

${\displaystyle \left|{\frac {1}{2\pi i}}\int _{\Gamma }{\frac {S_{N}(w)}{w-z}}dw-{\frac {1}{2\pi i}}\int _{\Gamma }{\frac {f(w)}{w-z}}dw\right|\leqslant }$

${\displaystyle {}\leqslant {\frac {1}{2\pi }}\int _{\Gamma }{\frac {|S_{N}(w)-f(w)|}{|w-z|}}|dw|\leqslant {\frac {\epsilon }{2\pi d}}2\pi 2d=2\epsilon }$.

По причине произвольности числа ${\displaystyle \epsilon >0}$ из последнего уравнения и последних неравенств для любого ${\displaystyle z}$ из ${\displaystyle d}$-окрестности имеем:

${\displaystyle \lim _{N\to \infty }S_{N}(z)={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {f(w)}{w-z}}dw}$.

то есть

${\displaystyle f(z)={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {S(w)}{w-z}}dw}$.

Правая часть последнего уравнения — интеграл типа Коши от непрерывной функции ${\displaystyle f(w)}$. По основному свойству он бесконечно дифференцируем, другими словами, сумма ряда ${\displaystyle f(z)}$ есть аналитическая функция в окрестности любой точки ${\displaystyle z_{0}\in D}$, следовательно, что сумма ряда ${\displaystyle f(z)}$ аналитична во всей области ${\displaystyle D}$.

В итоге получаем, что функции ${\displaystyle S_{N}(z)}$ и ${\displaystyle f(z)}$ аналитичны в области ${\displaystyle D}$, то есть, по теореме о бесконечной дифференцируемости, в ${\displaystyle D}$ имеются производные ${\displaystyle S_{N}^{(m)}(z)}$ и ${\displaystyle f^{(m)}(z)}$ при любом ${\displaystyle m\in \mathbb {N} }$.

1. Замкнутый контур. Построим вокруг произвольной точки ${\displaystyle z_{0}\in D}$ замкнутый кусочно-гладкий контур ${\displaystyle C}$ такой, что сам контур и его внутренность лежат в области ${\displaystyle D}$. На этом контуре ${\displaystyle C}$ данный ряд сходится равномерно по условию теоремы. Пусть ${\displaystyle w}$ — любая точка на контуре ${\displaystyle C}$, а ${\displaystyle z}$ — любая точка внутри контура ${\displaystyle C}$. Тогда разделим все члены ряда на разность ${\displaystyle (w-z)^{2}}$, получим ряд

${\displaystyle {\frac {f(w)}{(w-z)^{2}}}={\frac {f_{1}(w)}{(w-z)^{2}}}+}$

${\displaystyle {}+{\frac {f_{2}(w)}{(w-z)^{2}}}+\cdots +{\frac {f_{k}(w)}{(w-z)^{2}}}+\cdots }$,

который равномерно сходится для любых точек ${\displaystyle z\in C}$. Такой ряд, согласно теореме об интегрировании равномерно сходящегося ряда, почленно интегрируется вдоль замкнутой кривой ${\displaystyle C}$.

2. Интегрирование вдоль контура. Проинтегрируем ряд вдоль замкнутой кривой ${\displaystyle C}$, поделив все члены ряда на ${\displaystyle 2\pi i}$:

${\displaystyle {\frac {1}{2\pi i}}\int \limits _{C}{\frac {f(w)dw}{(w-z)^{2}}}={\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{1}(w)dw}{(w-z)^{2}}}+}$

${\displaystyle {}+{\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{2}(w)dw}{(w-z)^{2}}}+\cdots +{\frac {1}{2\pi i}}\int \limits _{C}{\frac {f_{k}(w)dw}{(w-z)^{2}}}+\cdots }$,

и поскольку функции ${\displaystyle f_{k}(z)}$ аналитические всюду внутри контура ${\displaystyle C}$ и на самом контуре по условию теоремы, то, по интегральной формуле Коши, перепишем последний ряд в следующем виде:

${\displaystyle f'(z)=f'_{1}(z)+f'_{2}(z)+\cdots +f'_{k}(z)+\cdots }$,

то есть ряд, составленный из производны от членов ряда в формулировке теоремы, сходится к производной от суммы того же ряда в любой точке ${\displaystyle z}$ внутри контура ${\displaystyle C}$, в частности, в точке ${\displaystyle z=z_{0}}$. Но ${\displaystyle z_{0}}$ — это, по определению, любая точка области ${\displaystyle D}$, следовательно, ряд можно почленно дифференцировать в любой точке области ${\displaystyle D}$. Теперь достаточно показать, что последний ряд, составленный из производны от членов ряда в формулировке теоремы, сходится равномерно в любой замкнутой области ${\displaystyle {\bar {D'}}}$, полностью находящейся в исходной области ${\displaystyle D}$, ${\displaystyle {\bar {D'}}\subset D}$.

3. Окрестность точки. Пусть теперь ${\displaystyle z_{0}}$ — любая точка замкнутой области ${\displaystyle {\bar {D'}}}$, ${\displaystyle z_{0}\in {\bar {D'}}}$. Построим окружность ${\displaystyle \Gamma }$ с центром в точке ${\displaystyle z_{0}}$ и такого маленького радиуса ${\displaystyle 2d}$, чтобы она вместе со своей внутренностью принадлежала области ${\displaystyle D}$. Построим также окрестность ${\displaystyle \sigma _{z_{0}}}$ точки ${\displaystyle z_{0}}$: ${\displaystyle |z-z_{0}|<d}$. Очевидно, что если точка ${\displaystyle w}$ движется по окружности ${\displaystyle \Gamma }$, а точка ${\displaystyle z}$ не выходит из окрестности ${\displaystyle \sigma _{z_{0}}}$, то расстояние между этими двумя точками ${\displaystyle |w-z|>d}$. Поскольку ряд в формулировке теоремы сходится равномерно на точках окружности ${\displaystyle \Gamma }$, то при произвольном сколь угодно малом ${\displaystyle \epsilon }$

${\displaystyle |f_{k+1}(w)+f_{k+2}(w)+\cdots |<\epsilon ,\quad k\geqslant N=N,(\epsilon )}$

для любой точки ${\displaystyle w\in \Gamma }$.

4. Равномерная сходимость. Применим последнее строгое неравенство к следующим членам ряда из производных, начиная с ${\displaystyle (n+1)}$-го:

${\displaystyle f'_{n+1}(z)+f'_{n+2}(z)+\cdots ={\frac {1}{2\pi i}}\int \limits _{\Gamma }{\frac {f_{n+1}(w)+f_{n+2}(w)+\cdots }{(w-z)^{2}}}dw}$,

получим:

${\displaystyle |f'_{n+1}(z)+f'_{n+2}(z)+\cdots |<{\frac {\epsilon 4\pi d}{2\pi d^{2}}}={\frac {2\epsilon }{d}}}$,

а это означает, что остаточный член ряда из производных, начиная с достаточно большого номера, меньше по модулю сколь угодно малого числа ${\displaystyle {\frac {2\epsilon }{d}}>0}$ независимо от точки ${\displaystyle z\in \sigma _{z_{0}}}$. Иначе говоря, доказано, что ряд из производных равномерно сходится в окрестности ${\displaystyle \sigma _{z_{0}}}$ любой точки ${\displaystyle z_{0}\in {\bar {D'}}}$. Следовательно, по лемме Гейне — Бореля область ${\displaystyle {\bar {D'}}}$ можно покрыть конечным числом окрестностей ${\displaystyle \sigma }$, причём в каждой из этих областей ряд из производных равномерно сходится. Поэтому ряд из производных

${\displaystyle f'(z)=f'_{1}(z)+f'_{2}(z)+\cdots +f'_{k}(z)+\cdots }$

равномерно сходится во всей области ${\displaystyle {\bar {D'}}}$.

5. Производные высших порядков. В силу соответствующей теоремы, производная аналитической функции — функция тоже аналитическая, следовательно, ряд

${\displaystyle f'(z)=f'_{1}(z)+f'_{2}(z)+\cdots +f'_{k}(z)+\cdots }$

представляет собой ряд функций, аналитических в области ${\displaystyle D}$, а также равномерно сходящийся в любой замкнутой области ${\displaystyle {\bar {D'}}\subset D}$. Применяя к этому ряду предыдущее доказательство, получаем:

${\displaystyle f''(z)=f''_{1}(z)+f''_{2}(z)+\cdots +f''_{k}(z)+\cdots }$,

и так далее, в итоге при любом ${\displaystyle m\in \mathbb {N} }$ имеем:

${\displaystyle f^{(m)}(z)=f_{1}^{(m)}(z)+f_{2}^{(m)}(z)+\cdots +f_{k}^{(m)}(z)+\cdots }$,

и кроме того, все эти ряды равномерно сходятся в любой замкнутой области ${\displaystyle {\bar {D'}}\subset D}$.

Пусть ${\displaystyle S_{N}(z)}$ — частичная сумма исходного ряда

${\displaystyle f(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{k}(z)+\cdots =\sum \limits _{k=1}^{\infty }f_{k}(z)}$,

то есть

${\displaystyle S_{N}(z)=f_{1}(z)+f_{2}(z)+\cdots +f_{N}(z)=\sum \limits _{k=1}^{N}f_{k}(z)}$.

1. Окрестность точки. Зафиксируем любую точку ${\displaystyle z_{0}}$ области ${\displaystyle D}$, ${\displaystyle z_{0}\in D}$. Построим любую ${\displaystyle d}$-окрестность ${\displaystyle |z-z_{0}|<d}$ точки ${\displaystyle z_{0}}$ такую, что её замыкание лежит в области ${\displaystyle D}$ и, кроме того, окружность ${\displaystyle \Gamma }$ с центром в точке ${\displaystyle z_{0}}$ и радиусом ${\displaystyle 2d}$ вместе со своей внутренностью принадлежит области ${\displaystyle D}$.

2. Равномерная сходимость. По теореме о бесконечной дифференцируемости при любом ${\displaystyle m\in \mathbb {N} }$ имеем для любой точки ${\displaystyle z}$ из замыкания ${\displaystyle d}$-окрестности ${\displaystyle |z-z_{0}|<d}$ и аналитических функций ${\displaystyle S_{N}(z)}$ и ${\displaystyle f(z)}$:

${\displaystyle S_{N}^{(m)}(z)={\frac {m!}{2\pi i}}\int \limits _{\Gamma }{\frac {S_{N}(w)}{(w-z)^{m+1}}}dw}$,

${\displaystyle f^{(m)}(z)={\frac {m!}{2\pi i}}\int \limits _{\Gamma }{\frac {f(w)}{(w-z)^{m+1}}}dw}$.

Далее, вследствие равномерной сходимости исходного ряда в замкнутом круге ${\displaystyle |z-z_{0}|\leqslant 2d}$ имеем, что для любого числа ${\displaystyle \epsilon >0}$ найдётся такое ${\displaystyle N(\epsilon )}$, что для любого ${\displaystyle N\leqslant N(\epsilon )}$ верно неравенство

${\displaystyle \sup _{w\in \Gamma }|S_{N}(w)-f(w)|<\epsilon }$.

Следовательно, для любого ${\displaystyle \epsilon >0}$ и любого ${\displaystyle N\geqslant N(\epsilon )}$ и для любой точки ${\displaystyle z}$ из замыкания ${\displaystyle d}$-окрестности ${\displaystyle |z-z_{0}|<d}$ получаем оценку

${\displaystyle |S_{N}^{(m)}(z)-f^{(m)}(z)|={\frac {m!}{2\pi }}\left|\int _{\Gamma }{\frac {S_{N}(w)-f(w)}{(w-z)^{m+1}}}dw\right|\leqslant }$

${\displaystyle {}\leqslant {\frac {m!}{2\pi d^{m+1}}}\sup _{w\in \Gamma }|S_{N}(w)-f(w)|2\pi 2d<{\frac {2m!}{d^{m}}}\epsilon }$.

Окончательно получаем, что последовательность частичных суии ${\displaystyle S_{N}^{(m)}(z)}$ сходится к функции ${\displaystyle f^{(m)}(z)}$ равномерно на замыкании ${\displaystyle d}$-окрестности. А поскольку точка ${\displaystyle z_{0}}$ и ${\displaystyle d}$-окрестность выбраны произвольно, то последовательность частичных суии ${\displaystyle S_{N}^{(m)}(z)}$ сходится к функции ${\displaystyle f^{(m)}(z)}$ равномерно в любой замкнутой области ${\displaystyle {\bar {D'}}\subset D}$.

1. Неравенства. Так как ряд с общим членом

${\displaystyle {\mathfrak {P}}_{m}(z)=\sum \limits _{k=0}^{\infty }c_{km}z^{k}}$

равномерно сходится на окружности круга ${\displaystyle K}$, то для любого числа ${\displaystyle \epsilon >0}$ имеется такое натуральное число ${\displaystyle N\in \mathbb {N} }$, что неравенство

${\displaystyle |{\mathfrak {P}}_{m+1}(z)+{\mathfrak {P}}_{m+2}(z)+\cdots +{\mathfrak {P}}_{m+l}(z)|\leqslant \epsilon }$

верно в любой точке ${\displaystyle z}$ окружности круга ${\displaystyle K}$ при произвольном ${\displaystyle l>0}$, когда ${\displaystyle m>N}$. Из этого неравенства по неравенству Коши для коэффициентов ряда Лорана вытекает неравенство

${\displaystyle |c_{k(m+1)}+c_{k(m+2)}+\cdots +c_{k(m+l)}|\leqslant {\frac {\epsilon }{\rho _{k}}},\quad k=0,\,1,\,2,\,\dots .}$

Поэтому сходятся следующие ряды:

${\displaystyle c_{k1}+c_{k2}+c_{k3}+\cdots =c_{k},\quad k=0,\,1,\,2,\,\dots .}$

Обозначим

${\displaystyle r_{km}=c_{k}-(c_{k1}+c_{k2}+\cdots +c_{km})}$,

тогда при ${\displaystyle m>N}$ верны также неравенства

${\displaystyle |r_{km}|\leqslant {\frac {\epsilon }{\rho _{k}}},\quad k=0,\,1,\,2,\,\dots .}$

2. Сходимость рядов. Пусть ${\displaystyle z}$ — любая тоска внутри круга ${\displaystyle K}$. Тогда ${\displaystyle |z|=\rho _{1}<\rho }$, поэтому сходится следующий ряд:

${\displaystyle \sum \limits _{k=0}^{\infty }(c_{k1}+c_{k2}+\cdots +c_{km})z^{k}={\mathfrak {P}}_{1}(z)+{\mathfrak {P}}_{2}(z)+\cdots +{\mathfrak {P}}_{m}(z)}$.

Кроме того, при ${\displaystyle m>N}$ сходится также и следующий ряд:

${\displaystyle \sum \limits _{k=0}^{\infty }r_{km}z^{k}={\mathfrak {O}}_{m}(z)}$,

поскольку, с учётом неравенства ${\displaystyle |r_{km}|\leqslant {\frac {\epsilon }{\rho _{k}}}}$, последний ряд мажорируется следующим сходящимся рядом:

${\displaystyle \sum \limits _{k=0}^{\infty }\epsilon \left({\frac {\rho _{1}}{\rho }}\right)^{k}={\frac {\epsilon }{1-\rho _{1}/\rho }}}$,

поэтому

${\displaystyle {\mathfrak {O}}_{m}(z)\leqslant {\frac {\epsilon }{1-\rho _{1}/\rho }}}$.

Следовательно, ряд

${\displaystyle \sum \limits _{k=0}^{\infty }c_{k}z_{k}={\mathfrak {P}}_{1}(z)+{\mathfrak {P}}_{2}(z)+\cdots +{\mathfrak {P}}_{m}(z)+{\mathfrak {O}}_{m}(z)={\mathfrak {P}}(z)}$

также сходится при заданном значении при ${\displaystyle z}$, причём при ${\displaystyle m>N}$ выполняется следующее неравенство:

${\displaystyle |{\mathfrak {P}}(z)-{\mathfrak {P}}_{1}(z)-{\mathfrak {P}}_{2}(z)-\cdots -{\mathfrak {P}}_{m}(z)|={\mathfrak {O}}_{m}(z)\leqslant {\frac {\epsilon }{1-\rho _{1}/\rho }}}$,

откуда, поскольку ${\displaystyle \epsilon }$ любое, имеем равенство

${\displaystyle {\mathfrak {P}}(z)={\mathfrak {P}}_{1}(z)+{\mathfrak {P}}_{2}(z)+\cdots +{\mathfrak {P}}_{k}(z)+\cdots }$,

что и требовалось доказать.