Эллиптическая система координат

Эллиптические координаты — двумерная ортогональная система координат, в которой координатными линиями являются конфокальные эллипсы и гиперболы. За два фокуса $F_{1}$ и $F_{2}$ обычно берутся точки $-c$ и $+c$ на оси $X$ декартовой системы координат.

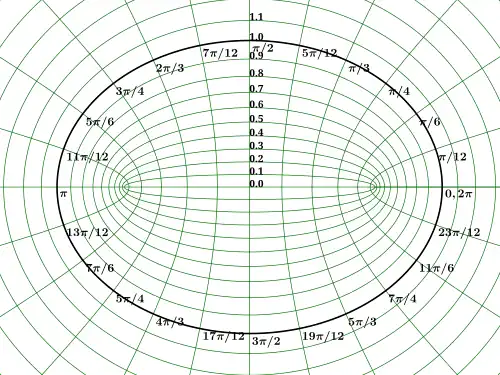
Основное определение

Эллиптические координаты $(\mu ,\;\nu )$ обычно определяются по правилу:

\left\{{\begin{matrix}x=c\,\mathrm {ch} \,\mu \cos \nu \\y=c\,\mathrm {sh} \,\mu \sin \nu \end{matrix}}\right.

где $\mu \geqslant 0$ , $\nu \in [0,\;2\pi )$ .

Таким образом определяется семейство конфокальных эллипсов и гипербол. Тригонометрическое тождество

{\frac {x^{2}}{c^{2}\,\mathrm {ch} ^{2}\,\mu }}+{\frac {y^{2}}{c^{2}\,\mathrm {sh} ^{2}\,\mu }}=\cos ^{2}\nu +\sin ^{2}\nu =1

показывает, что линии уровня $\mu$ являются эллипсами, а тождество из гиперболической геометрии

{\frac {x^{2}}{c^{2}\cos ^{2}\nu }}-{\frac {y^{2}}{c^{2}\sin ^{2}\nu }}=\mathrm {ch} ^{2}\,\mu -\mathrm {sh} ^{2}\,\mu =1

показывает, что линии уровня $\nu$ являются гиперболами.

Коэффициенты Ламэ

Коэффициенты Ламэ для эллиптических координат $(\mu ,\;\nu )$ равны

H_{\mu }=H_{\nu }=c{\sqrt {(\mathrm {ch} \,\mu \,\sin \,\nu )^{2}+(\mathrm {sh} \,\mu \,\cos \,\nu )^{2}}}=c{\sqrt {\mathrm {sh} ^{2}\,\mu +\sin ^{2}\nu }}.

Тождества для двойного угла позволяют привести их к виду

H_{\mu }=H_{\nu }=c{\sqrt {{\frac {1}{2}}(\mathrm {ch} \,2\mu -\cos 2\nu }}).

Элемент площади равен:

dS=c^{2}(\mathrm {sh} ^{2}\,\mu +\sin ^{2}\nu )\,d\mu \,d\nu ,

а лапласиан равен

\nabla ^{2}\Phi ={\frac {1}{c^{2}(\mathrm {sh} ^{2}\,\mu +\sin ^{2}\nu )}}\left({\frac {\partial ^{2}\Phi }{\partial \mu ^{2}}}+{\frac {\partial ^{2}\Phi }{\partial \nu ^{2}}}\right).

Прочие дифференциальные операторы могут быть получены подстановкой коэффициентов Ламэ в общие формулы для ортогональных координат. Например, градиент скалярного поля $\Phi (\mu ,\;\nu )$ записывается:

\mathrm {grad} \,\Phi ={\frac {1}{H_{\mu }}}{\frac {\partial \Phi }{\partial \mu }}\mathbf {e} _{\mu }+{\frac {1}{H_{\nu }}}{\frac {\partial \Phi }{\partial \nu }}\mathbf {e} _{\nu },

где

\mathbf {e} _{\mu }=c(\mathrm {sh} \,\mu \cos \nu ,\,\mathrm {ch} \,\mu \sin \nu )

,

\mathbf {e} _{\nu }=c(-\mathrm {ch} \,\mu \sin \nu ,\,\mathrm {sh} \,\mu \cos \nu )

.

Другое определение

Иногда используется другое более геометрически интуитивное определение эллиптических координат $(\sigma ,\;\tau )$ :

\left\{{\begin{matrix}\sigma =\mathrm {ch} \,\mu \\\tau =\cos \nu \end{matrix}}\right.

Таким образом, линии уровня $\sigma$ являются эллипсами, а линии уровня $\tau$ являются гиперболами. При этом

\tau \in [-1,\;1],\quad \sigma \geqslant 1.

Координаты $(\sigma ,\;\tau )$ имеют простую связь с расстояниями до фокусов $F_{1}$ и $F_{2}$ . Для любой точки на плоскости

\left\{{\begin{matrix}d_{1}+d_{2}=2c\sigma \\d_{1}-d_{2}=2c\tau \end{matrix}}\right.

где $d_{1},\;d_{2}$ — расстояния до фокусов $F_{1},\;F_{2}$ соответственно.

Таким образом:

\left\{{\begin{matrix}d_{1}=c(\sigma +\tau )\\d_{2}=c(\sigma -\tau )\end{matrix}}\right.

Напомним, что $F_{1}$ и $F_{2}$ находятся в точках $x=-c$ и $x=+c$ соответственно.

Недостатком этой системы координат является то, что она не отображается взаимно однозначно на декартовы координаты:

\left\{{\begin{matrix}x=c\sigma \tau \\y^{2}=c^{2}(\sigma ^{2}-1)(1-\tau ^{2})\end{matrix}}\right.

Коэффициенты Ламэ

Коэффициенты Ламэ для альтернативных эллиптических координат $(\sigma ,\;\tau )$ равны:

h_{\sigma }=c{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{\sigma ^{2}-1}}};

h_{\tau }=c{\sqrt {\frac {\sigma ^{2}-\tau ^{2}}{1-\tau ^{2}}}}.

Элемент площади равен

dA=c^{2}{\frac {\sigma ^{2}-\tau ^{2}}{\sqrt {(\sigma ^{2}-1)(1-\tau ^{2})}}}\,d\sigma \,d\tau ,

а лапласиан равен

\nabla ^{2}\Phi ={\frac {1}{c^{2}(\sigma ^{2}-\tau ^{2})}}\left[{\sqrt {\sigma ^{2}-1}}{\frac {\partial }{\partial \sigma }}\left({\sqrt {\sigma ^{2}-1}}{\frac {\partial \Phi }{\partial \sigma }}\right)+{\sqrt {1-\tau ^{2}}}{\frac {\partial }{\partial \tau }}\left({\sqrt {1-\tau ^{2}}}{\frac {\partial \Phi }{\partial \tau }}\right)\right].

Прочие дифференциальные операторы могут быть получены подстановкой коэффициентов Ламэ в общие формулы для ортогональных координат.

Литература

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1974. — 832 с.

См. также

Окружность Аполлония

Системы координат
Название координат	Абсцисса Ордината Аппликата
Типы систем координат	Прямолинейная система координат Криволинейная система координат
Двумерные координаты	Биангулярные координаты Бицентрические координаты Гиперболические координаты Полярные координаты Биполярные координаты Параболические координаты Эллиптические координаты Тетрациклические координаты Трилинейные координаты
Трёхмерные координаты	Цилиндрические координаты Сферические координаты Бисферические координаты Тороидальные координаты Цилиндрические параболические координаты Бицилиндрические координаты Эллипсоидальные координаты Конические координаты Пентасферические координаты Диполярная система координат
$n$ -мерные координаты	Декартовы координаты Аффинные координаты Проективные координаты Плюккеровы координаты Барицентрические координаты
Физические координаты	Координаты Риндлера Координаты Борна Система небесных координат Географические координаты Главноортодромическая система координат
Связанные определения	Метод координат Начало координат Координатная ось Вектор Орт Система отсчёта Репер Коэффициенты Ламе Метрический тензор