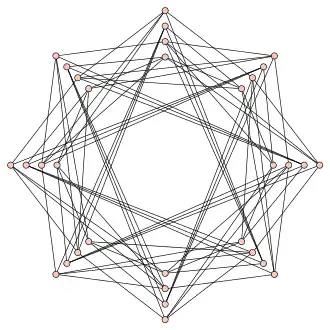
Граф Уэлса

Граф Уэлса
Граф Уэлса
Вершин	32
Рёбер	89
Диаметр	5
Обхват	5
Автоморфизмы	1920
Хроматическое число	4
Хроматический индекс	5
Свойства	Дистанционно-регулярный; Гамильтонов
Число очередей	3

Граф Уэлса — единственный дистанционно-регулярный граф с массивом пересечений $\{5,4,1,1;1,1,4,5\}$ ^[1].

Спектр графа равен $5^{1}{\sqrt {5}}^{8}1^{1}0(-{\sqrt {5}})^{8}(-3)^{5}$ и существует ещё два графа с тем же спектром^[2]. Его число очередей равно 3, а верхняя граница книжной толщины равна 5^[3].

Примечания

↑ Brouwer A. E., Cohen A. M., Neumaier first3 = A. Theorem 9.2.9 // Distance-regular graphs. — Springer-Verlag, 1989.
↑ van Dam E. R., Haemers W. H. Spectral Characterizations of Some Distance-Regular Graphs // J. Algebraic Combin.. — 2003. — Вып. 15. — С. 189—202.
↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

Ссылки

A.E. Brouwer’s website: The Armanios-Wells graph Архивная копия от 14 апреля 2018 на Wayback Machine

[Brouwer-1] Brouwer A. E., Cohen A. M., Neumaier first3 = A. Theorem 9.2.9 // Distance-regular graphs. — Springer-Verlag, 1989.

[vDH-2] van Dam E. R., Haemers W. H. Spectral Characterizations of Some Distance-Regular Graphs // J. Algebraic Combin.. — 2003. — Вып. 15. — С. 189—202.

[Wolz-3] Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018

[1]

[2]

[3]