Правильный 5-симплекс
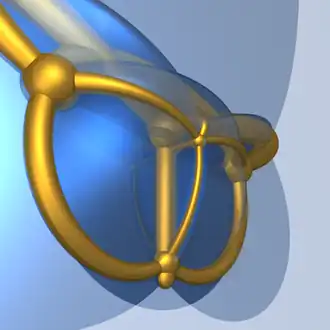
| Гексатерон (правильный 5-симплекс) | |
|---|---|
 | |
| Тип | Правильный пятимерный политоп |
| Символ Шлефли | {3,3,3,3} |
| Диаграмма Коксетера — Дынкина | |
| 4-мерных ячеек | 6 |
| Ячеек | 15 |
| Граней | 20 |
| Рёбер | 15 |
| Вершин | 6 |
| Вершинная фигура | 5-ячейник |
| Двойственный политоп | Он же |
Правильный 5-симплекс, или правильный гексатерон, или просто гексатерон[1] — пятимерное геометрическое тело, правильный политоп, ограниченный шестью гранями-пятиячейниками. Представляет собой пятимерный вариант правильного симплекса.
Состоит из 6 4-мерных граней-пятиячейников, 15 правильнотетраэдрических ячеек, 20 граней — правильных треугольников, 15 рёбер и 6 вершин. Одна из множества проекций правильного 5-симплекса на плоскость — шестиугольник с вписанной в него гексаграммой. Двугранный угол гексатерона равен arccos(0,2), то есть примерно 78,46°.
В прямоугольной системе координат
Гексатерон может быть получен из пятиячейника путём добавления шестой вершины, равноудалённой от всех других вершин исходного пятиячейника. Гексатерон можно разместить в Декартовой системе координат следующим образом (длина ребра тела равна 2):
Примечания
- ↑ Jonathan Bowers. Uniform Polytera and Other Five Dimensional Shapes. Дата обращения: 22 октября 2016. Архивировано 18 сентября 2020 года.
Литература
- Александров П. С. Комбинаторная топология, М. — Л., 1947